python - 装箱项目/3D Bin Packing problem
python装箱问题/3D Bin Packing problem
- 一、从商业角度看自主且可控是十分重要的
- 1. 市场上常见的3D装箱软件&收费情况
- 二、实现逻辑
- 2.1 **python package**:
- 2.2 **流程模块**
- a) 首先是基础信息:有待装箱的box、容器container信息;
- b) 然后是自定义算法:又快又好的把box放入container;
- c) 最后是可视化:将结果用3D呈现并可拖拽旋转;
- 三、实现方案
- 3.1 基础信息
- 3.2 流程模块
- a) 引入库包和模型
- b) 整理箱子信息
- c) 箱子是否装入容器,是的话如何摆放,并且在容器内
- d) ==核心约束==:手动实现3D NoOverlap,即不重叠约束
- e) 目标函数
- f) 获取结果
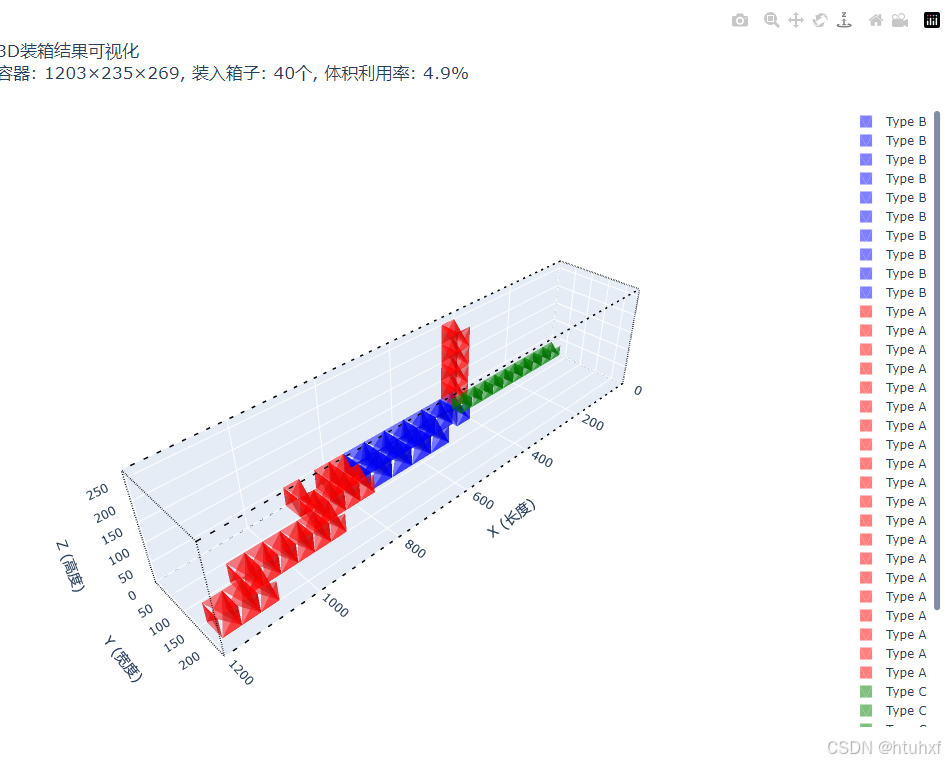
- 3.3 可视化
一、从商业角度看自主且可控是十分重要的
目前python并没有现成的针对“装箱问题 / 3D bin packing”的package包,市场上存在收费的软件,但是使用过ERP系统的都知道,基础标签的更新都需要上万元,更别提功能模块的更新,叠加厂家派人来的按天工费是笔不小的开支。因此搞一个自主可控无各种限制且免费版的装箱产品是比较经济的,也是可行的。
本文深度参考知乎“人类个体”的《从零构建三维装箱问题求解器》,如有侵权请联系。
1. 市场上常见的3D装箱软件&收费情况
| 名称 | 价格 | 收费类型 | 简介 |
|---|---|---|---|
| Optimal Pack | 价格约5000RMB/年,或者12RMB/箱 | 提供免费试用版每日6箱。 | 在线打开即用。针对企业级需求,支持定制开发、本地部署及API系统接入 |
| Packly | 约0.5-2美元/次 | 基础功能免费;高级功能按次收费(如导出报告) | 简单易用的在线工具,适合电商和小型物流需求 |
| LoadMaster | 基础版约2000$/年 | 提供免费试用版,正式版价格根据功能模块定制 | 专注于集装箱和卡车装载优化,支持多种货物类型和运输方式 |
| EasyCargo | 约200$/年起 | 免费版功能有限;付费版按月订阅,付费版按月订阅,企业版需联系销售定价 | 在线3D装箱工具,支持多语言和多种运输方式,适合中小型企业 |
| PackApp | 约250$/年起 | 需定制报价,通常按用户数和模块收费 | 专业级物流优化软件,涵盖装箱、路线规划等,适合大型企业 |
| Cube-IQ | 年费可达数万美元 | 需联系销售获取报价 | 专注于卡车和集装箱装载,支持3D可视化与多约束条件优化 |
二、实现逻辑
2.1 python package:
google OR-Tools链接请点击。OR-Tools 是一种用于组合优化的开源软件,该软件力求从一组可能的大量解决方案中找出某个问题的最佳解决方案。以下是 OR 工具可以解决的一些问题示例:
- 车辆路线:根据给定的限制条件(例如,“这辆卡车承载的重量不能超过 20,000 磅”或“所有送货都必须在两小时内完成”)。
- 调度:为一组复杂的任务找到最佳调度,其中一些任务需要先完成,然后才能在一组固定的机器或其他资源上执行。
- 箱装:将各种不同尺寸的对象装入具有最大容量的固定数量的箱中。
2.2 流程模块
a) 首先是基础信息:有待装箱的box、容器container信息;
- 集装箱信息:{类型, 长, 宽, 高, 数量}
- 待装箱box信息:{类型, 长, 宽, 高, 数量}
b) 然后是自定义算法:又快又好的把box放入container;
- 核心python包:OR-Tools
- 代码逻辑
– 1st 建模阶段:获取引入模型,搜集所有变量和约束。其中约束主要是是否装箱约束、箱子朝向约束和非重叠约束;
– 2nd 求解阶段:统一处理所有约束,寻找满足所有条件的解
c) 最后是可视化:将结果用3D呈现并可拖拽旋转;
- 核心python包:Plotly
三、实现方案
3.1 基础信息
- 容器选择40HQ集装箱: container_dimensions= (1203, 235, 269)
- box输入:自定义为box_type_input = [
{“type_name”: “A”, “l”: 50, “w”: 40, “h”: 50, “quantity”: 20},
{“type_name”: “B”, “l”: 45, “w”: 60, “h”: 50, “quantity”: 10},
{“type_name”: “C”, “l”: 40, “w”: 30, “h”: 30, “quantity”: 10},
{“type_name”: “D”, “l”: 50, “w”: 50, “h”: 40, “quantity”: 50}
]
3.2 流程模块
第一部分:主要是引入库包,添加箱子是否要装箱、装的话摆放的朝向。相比原文,通过消除对称解提升19%~30%性能。
a) 引入库包和模型
from ortools.sat.python import cp_modelmodel = cp_model.CpModel() # 创建模型
b) 整理箱子信息
for instance in range(bt['quantity']放入内循环,结合.extend()进行性能优化
# 获取所有box以list形式储存,统计个数N
all_boxes = []
for bt in box_type_input:type_name = bt['type_name']l, w, h = bt['l'], bt['w'], bt['h']volume = l*w*hboxes_batch =[{'type_name': type_name,'l':l, 'w':w, 'h':h,'volume': volume,'instance_id': instance}for instance in range(bt['quantity'])]all_boxes.extend(boxes_batch)N = len(all_boxes)
print(f"Created variables for {N} box instances.")
c) 箱子是否装入容器,是的话如何摆放,并且在容器内
-
打破优化模型中的“体积对称性”。通过对同体积箱子施加逻辑优先级约束,减少冗余解空间,加速求解过程
- 减少搜索空间:将同体积箱子的组合可能性从 2^k(无约束)降至 k+1(k为同体积箱子数量,即“连续选中前0/1/2/…/k个”)。
- 加速最优解收敛:求解器无需在对称解之间反复回溯,可更快聚焦于真正影响目标函数的关键选择。
-
约束》每个箱子选择一个方向,按6个朝向举例
- b[k] = 1 p_k = [0, 1, 0, 0, 0, 0] → sum(p_k)必须为1 → 恰好一个p_k[j]为1,其他为0
- b[k] = 1, p_k = [1, 1, 0, 0, 0, 0] → sum=2 ≠ 1 → 冲突!
""" part1 箱子是否装入容器,并消除对称解提升求解效率"""
# 按体积先排序,可优化
all_boxes.sort(key=lambda x: x['volume'], reverse=True)
# 生成变量。是否装箱
b = [model.NewBoolVar(f'b_{k}') for k in range(N)]# 消除对称解提升求解效率。
for i in range(N-1):if all_boxes[i]['volume'] == all_boxes[i+1]['volume']:model.Add(b[i] >= b[i+1])L, W, H = container_dims
# 生成变量。顶点坐标
x = [model.NewIntVar(0, L, f'x_{k}') for k in range(N)]
y = [model.NewIntVar(0, W, f'y_{k}') for k in range(N)]
z = [model.NewIntVar(0, H, f'z_{k}') for k in range(N)]
""" part2 约束每个箱子选择一个朝向"""
# 箱子方向j和个数P。
orientations = [(0, 1, 2), (1, 0, 2)] # j1和j2共计两个。一共6种但实际中上朝向一般不能变;
P = len(orientations )l_actual_vars = [None]*N
w_actual_vars = [None]*N
h_actual_vars = [None]*N
for k, box in enumerate(all_boxes): # box={'type_name', 'l', 'w', 'h', 'volume', 'instance_id'}p_k = [model.NewBoolVar(f'b_{k}_{j}') for j in range(P)] # 是否是j朝向摆放model.Add(sum(p_k)==b[k])original_dims =[box['l'], box['w'], box['h']]# 常量l_options = [ original_dims[orientations[j][0]] for j in range(P) ]w_options = [ original_dims[orientations[j][1]] for j in range(P) ]h_options = [ original_dims[orientations[j][2]] for j in range(P) ]# 生成变量。 $$ \varDelta{l} $$ $$ \varDelta{w} $$ $$ \varDelta{h} $$l_actual = model.NewIntVar(1, max(original_dims), f'l_actual_{k}')w_actual = model.NewIntVar(1, max(original_dims), f'w_actual_{K}')h_actual = model.NewIntVar(1, max(original_dims), f'h_actual_{k}')l_actual_vars[k] = l_actual # 是变量对象的引用,l_actual_vars[k] 和 l_actual 指向同一个变量对象w_actual_vars[k] = w_actualh_actual_vars[k] = h_actualpos_index = model.NewIntVar(0, P-1, f'pos_index_{k}')# 约束》旋转后实际坐标上l/w/h的长度for j in range(P):model.Add(pos_index==j).OnlyEnforceIf(p_k[j])model.AddElement(pos_index, l_options, l_actual)model.AddElement(pos_index, w_options, w_actual)model.AddElement(pos_index, h_options, h_actual)
""" part3 约束box要在容器内"""model.Add(x[k] + l_actual <= L).OnlyEnforceIf(b[k])model.Add(y[k] + w_actual <= W).OnlyEnforceIf(b[k])model.Add(z[k] + h_actual <= H).OnlyEnforceIf(b[k])
d) 核心约束:手动实现3D NoOverlap,即不重叠约束
for i in range(N-1):for j in range(i+1, N):sep_vars = {}locations = ['x_left', 'x_right', 'y_front', 'y_back', 'z_below', 'z_above']for loc in directions:sep_vars[loc] = model.NewBoolVar(f'sep_{loc}_{i}_{j}')# x维度分离model.Add(x[i] + l_actual_vars[i] <= x[j]).OnlyEnforceIf(sep_vars ['x_left'])model.Add(x[j] + l_actual_vars[j] <= x[i]).OnlyEnforceIf(sep_vars['x_right'])# y维度分离model.Add(y[i] + w_actual_vars[i] <= y[j]).OnlyEnforceIf(sep_vars[ 'y_front'])model.Add(y[j] + w_actual_vars[j] <= y[i]).OnlyEnforceIf(sep_vars['y_back'])# z维度分离model.Add(z[i] + h_actual_vars[i] <= z[j]).OnlyEnforceIf(sep_vars['z_below'])model.Add(z[j] + h_actual_vars[j] <= z[i]).OnlyEnforceIf(sep_vars['z_above'])
e) 目标函数
# 最大化装箱体积
if maximize_volume:total_volume = sum(b[k] * all_boxes[k]['volume'] for k in range(N))model.Maxmize(total_volume)
# 最大化装箱数量
else:total_boxes_num = sum(b[k] for k in range(N))model.Maxmize(total_boxes_num)# --- 求解 ---
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = time_limit_seconds
solver.parameters.log_search_progress = True
solver.parameters.num_search_workers = 8status = solver.Solve(model)
f) 获取结果
results = []
total_volume = 0if status == cp_model.OPTIMAL or status ==cp_model.FEASIBLE:print(f'求解状态:{"最优解" if status==cp_model.OPTIMAL else "可行解"}')print(f'求解时间:{solver.WallTime():.2f} 秒')print(f'目标值:{solver.ObjectiveValue()}')for k in range(N):if solver.Value(b[k]):box = all_boxes[k]x_val = solver.Value(x[k])y_val = solver.Value(y[k])z_val = solver.Value(z[k])l_val = solver.Value(l_actual_vars[k])w_val = solver.Value(w_actual_vars[k])h_val = solver.Value(h_actual_vars[k])volume = l_val * w_val * h_valtotal_volume += volume# 获取摆放的朝向for j in range(P):if solver.Value(p_k[j]):orientatioin = jbreakresults.append({"箱子编号": k,"类型": box['type_name'],"实例": box['instance_id'],"X坐标": x_val,"Y坐标": y_val,"Z坐标": z_val,"长": l_val,"宽": w_val,"高": h_val,"体积": volume,"方向": orientation,"原始尺寸": f"{box['l']}x{box['w']}x{box['h']}"})result_df = pd.DataFrame(results)
3.3 可视化