当前位置：首页 > news >正文

旅行商问题（TSP）（2）（heuristics.py）（TSP 的两种贪心启发式算法实现）

news 2025/10/14 10:57:30

旅行商问题从实现到测试

共四篇博客分别讲解，四篇的内容分别是

1.TSP 问题中的点与路径核心类

2.TSP 的两种贪心启发式算法实现（最近邻算法和最近插入算法）

3.TSP 项目的 “时间统计与属性注入” 工具

4.TSP 项目的测试验证体系

在旅行商问题（TSP）中，由于 “找到最优解” 的复杂度极高，实际应用中常使用启发式算法（贪心策略）快速得到近似解。heuristics.py 文件实现了两种核心的贪心算法：最近邻点法和最近插入法。

heuristics.py 完整代码在文章末尾

代码源：旅行商问题（TSP）代码和数据资源-CSDN下载

一、算法前置知识：装饰器 @display_time

在看算法之前，先注意每个算法函数上方的 @display_time 装饰器 —— 它来自 decorator.py，核心作用是：

统计算法的运行时间；
自动为输出的 Route 对象注入 run_time（运行时间）和 algo_name（算法名）属性；
打印算法的运行结果（运行时间、路径总距离）。

装饰器的存在让算法代码更简洁，无需手动处理时间统计和属性注入，后续在 Lab_test.py 中调用算法时，能直接获取时间和路径信息。

二、最近邻点法（nearestNeighbor）

1. 算法核心思想

从指定的起点出发，每次选择 “当前点的最近未访问点” 作为下一个点，直到所有点都被访问，最后回到起点形成闭合路径。

贪心逻辑：每一步只关注 “当前最优”（最近的点），不考虑后续步骤的影响，因此不一定能得到全局最优解，但计算速度快。

2. 代码实现与解析

@display_time
def nearestNeighbor(pointsL, startPoint):"""最近邻算法：从起点出发，每次选择最近未访问点（案例图2逻辑）"""# 第一步：输入验证（确保参数符合要求，避免后续错误）if not isinstance(startPoint, Point):raise TypeError("startPoint must be a Point instance")if startPoint not in pointsL:raise ValueError("startPoint must be in pointsL")# 第二步：初始化“未访问点列表”和“路径列表”unvisited = pointsL.copy()  # 复制所有点，作为未访问集合unvisited.remove(startPoint)  # 移除起点（起点已访问）path = [startPoint]  # 路径从起点开始current = startPoint  # 当前所在的点（初始为起点）# 第三步：核心循环——反复选择最近未访问点，直到所有点被访问while unvisited:  # 当还有未访问点时# 找到未访问点中距离当前点最近的点（用min+lambda，以距离为排序依据）closest = min(unvisited, key=lambda p: current.dist_to_point(p))# 将最近点加入路径path.append(closest)# 从“未访问列表”中移除该点（标记为已访问）unvisited.remove(closest)# 更新当前点为刚加入的最近点current = closest# 第四步：闭合路径——最后回到起点path.append(startPoint)# 第五步：返回路径（封装成Route对象，符合输出要求）return Route(path)

3. 关键步骤拆解

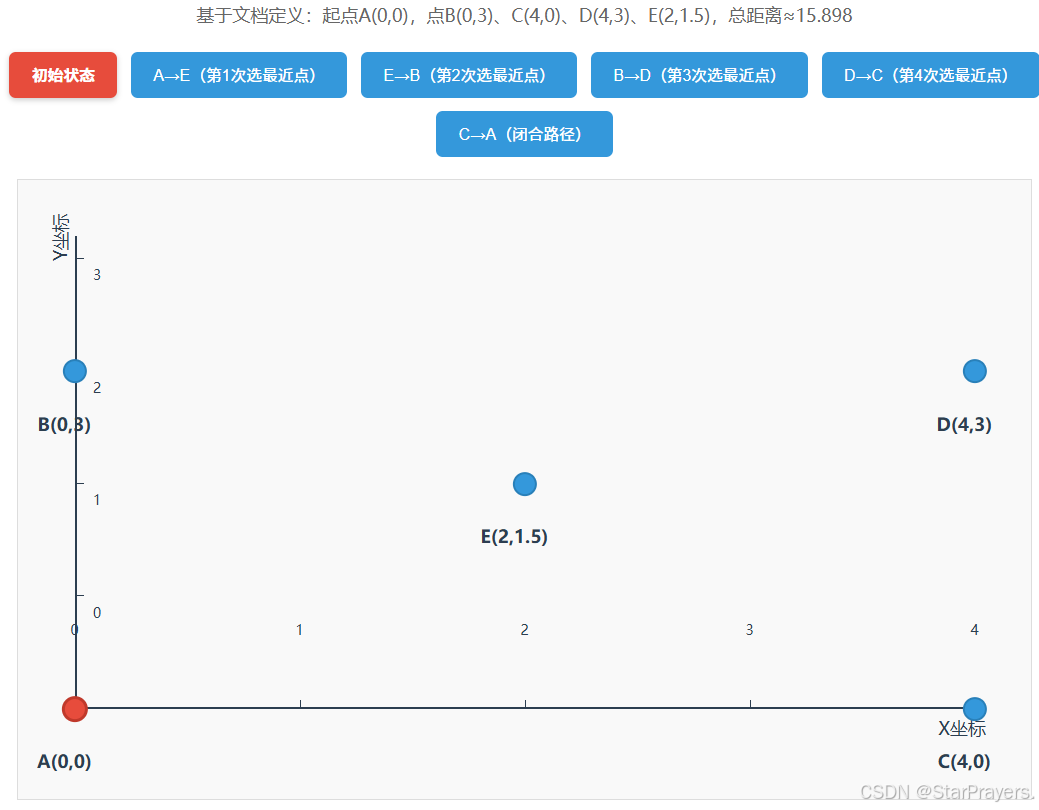
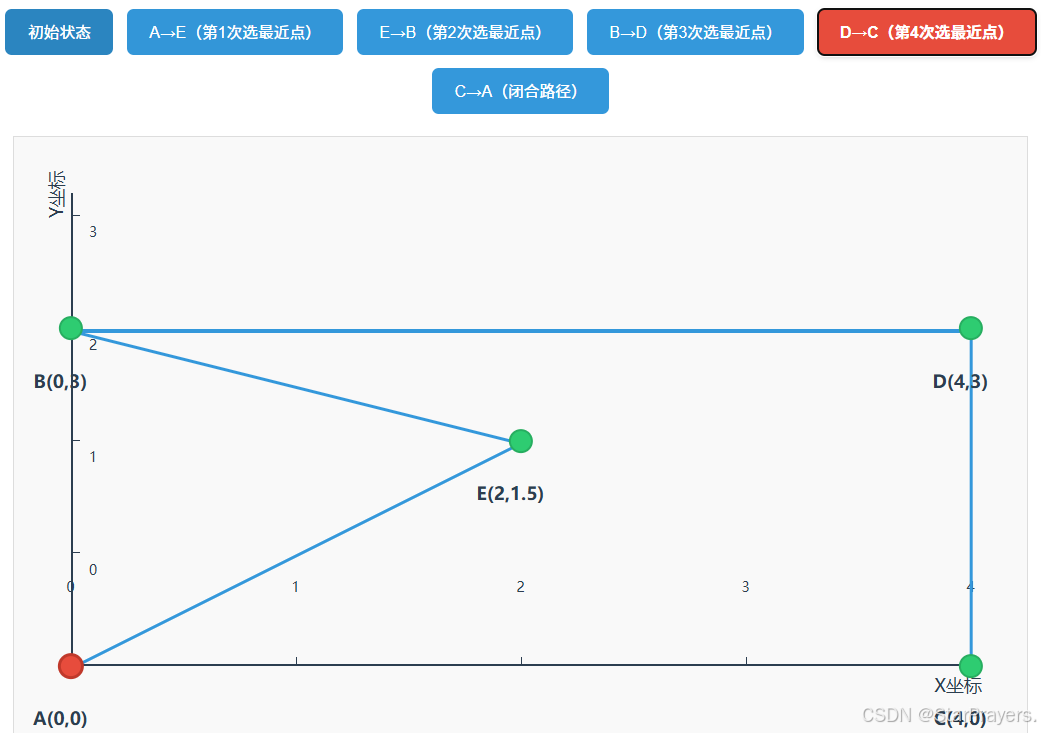
以 “5 点用例”（A (0,0)、B (0,3)、C (4,0)、D (4,3)、E (2,1.5)）、起点为 A 为例，手动走一遍流程：

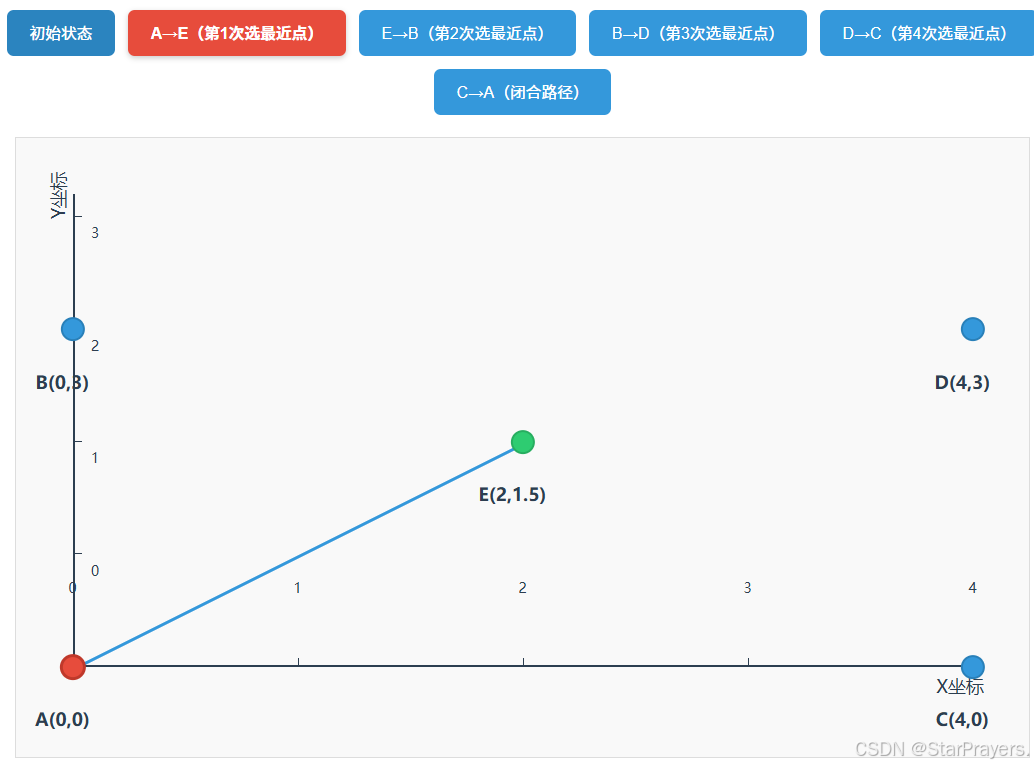
初始化：unvisited = [B,C,D,E]，path = [A]，current = A；
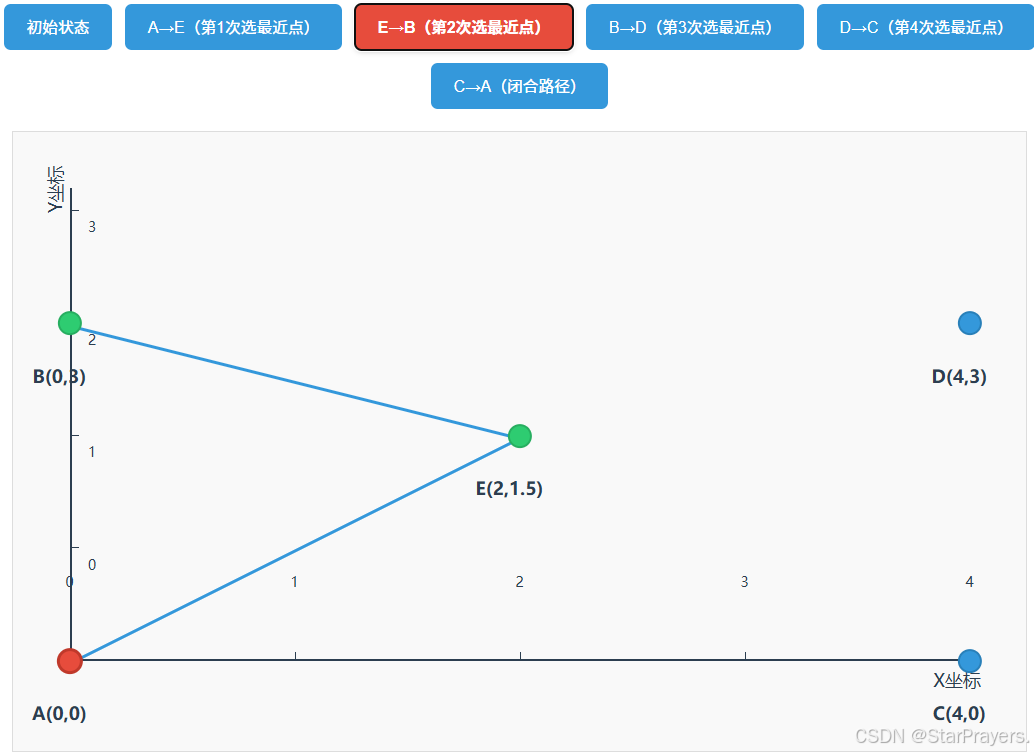
第一次循环：A 的最近未访问点是 E（距离≈2.5），path 变为 [A,E]，unvisited 变为 [B,C,D]，current = E；
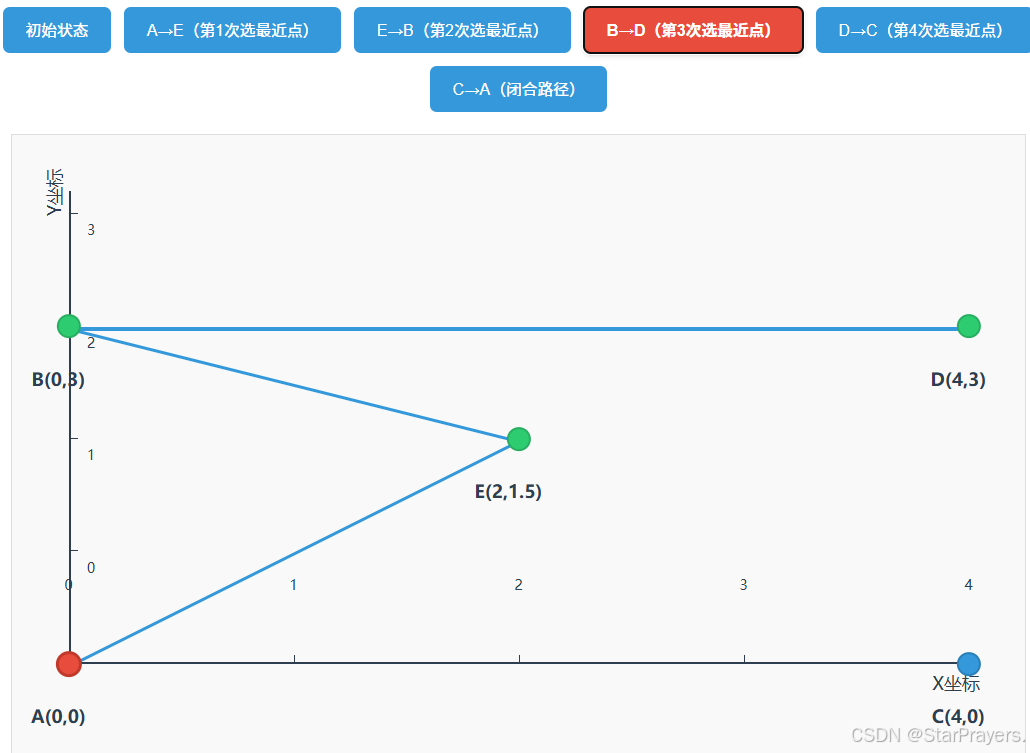
第二次循环：E 的最近未访问点是 B（距离≈2.5），path 变为 [A,E,B]，unvisited 变为 [C,D]，current = B；
第三次循环：B 的最近未访问点是 D（距离 = 4），path 变为 [A,E,B,D]，unvisited 变为 [C]，current = D；
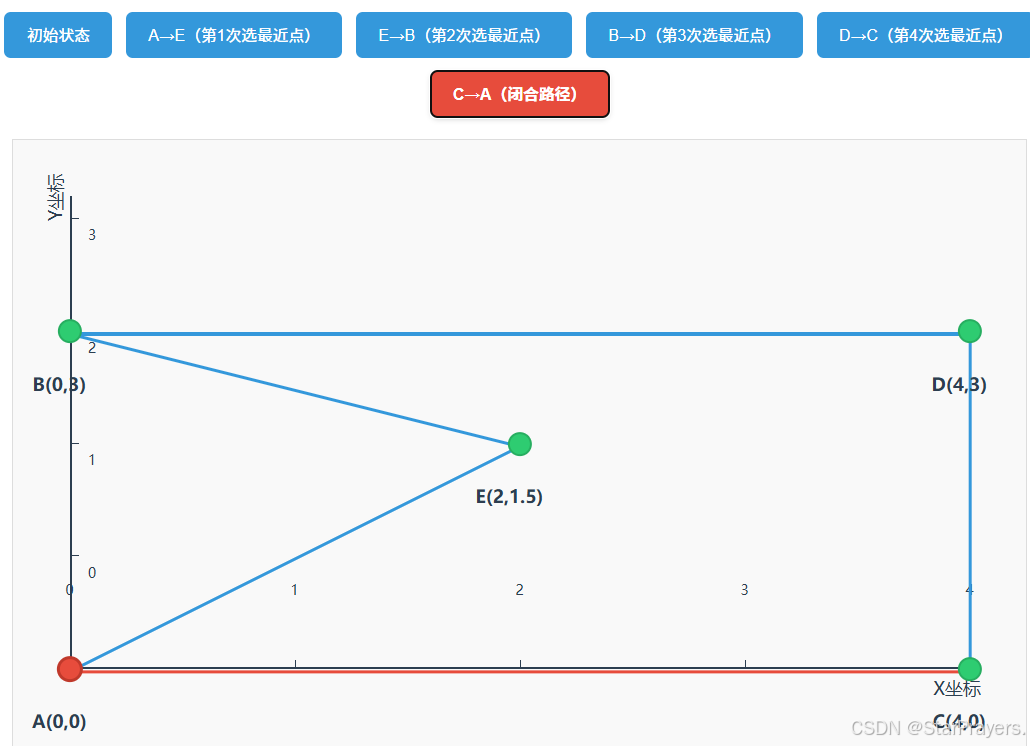
第四次循环：D 的最近未访问点是 C（距离 = 3），path 变为 [A,E,B,D,C]，unvisited 为空；
闭合路径：path 最终为 [A,E,B,D,C,A]，总距离≈15.898（与 Lab_test.py 中的预期结果一致）。

4.最近邻算法（nearestNeighbor）过程图

网页文件：5点用例最近邻算法流程可视化（Prayer）.html资源-CSDN下载

5. 算法特点

优点：逻辑简单，代码短，计算速度快（时间复杂度 O (n²)，n 为点的数量）；
缺点：易陷入 “局部最优”，最终路径总距离可能较长（如上述例子中，若起点不同，路径可能更优）。

三、最近插入法（nearestInsertion）

1. 算法核心思想

与最近邻法不同，最近插入法从 “两个起点构成的初始路径” 出发，每次找到 “距离当前路径最近的未访问点”，并将其插入到 “使路径总长度增量最小” 的位置，直到所有点被访问，最后回到起点。贪心逻辑：不仅关注 “选哪个点”，还关注 “插在哪里”，因此通常比最近邻法得到的路径更优（总距离更短），但计算量稍大。

2. 代码实现与解析

@display_time
def nearestInsertion(pointsL, startPoint1, startPoint2):"""最近插入算法：从两个起点出发，插入最近点并最小化路径增量（案例图3逻辑）"""# 第一步：输入验证（确保两个起点不同且都在点列表中）if startPoint1 == startPoint2:raise ValueError("Start points must be different")if startPoint1 not in pointsL or startPoint2 not in pointsL:raise ValueError("Start points must be in pointsL")# 第二步：初始化“路径列表”和“剩余未访问点列表”path = [startPoint1, startPoint2]  # 初始路径是两个起点（如A→B）remaining = [p for p in pointsL if p not in path]  # 未访问的点（排除两个起点）# 第三步：核心循环——选最近点→找最小插入位置→插入，直到所有点被访问while remaining:# 子步骤1：找到距离当前路径最近的未访问点# 定义“点到路径的距离”：点到路径中所有点的最小距离def dist_to_path(point):return min(point.dist_to_point(p) for p in path)# 用min找到“距离路径最近”的点best_point = min(remaining, key=dist_to_path)# 子步骤2：找到插入该点后，路径总长度增量最小的位置min_increase = math.inf  # 初始化“最小增量”为无穷大best_pos = 0  # 初始化“最优插入位置”为0# 遍历路径中的每一段（如路径[A,B,D]的段是A→B、B→D）for i in range(len(path)):a, b = path[i], path[(i + 1) % len(path)]  # a是段的起点，b是段的终点（%处理循环）original_dist = a.dist_to_point(b)  # 原段的距离（a→b）new_dist = a.dist_to_point(best_point) + best_point.dist_to_point(b)  # 插入后的距离（a→best_point→b）increase = new_dist - original_dist  # 插入导致的距离增量（越小越好）# 更新“最小增量”和“最优位置”if increase < min_increase:min_increase = increasebest_pos = i + 1  # 插入位置在a和b之间（即i+1索引）# 子步骤3：将最优点点插入路径，并从剩余列表中移除path.insert(best_pos, best_point)remaining.remove(best_point)# 第四步：闭合路径——回到第一个起点path.append(startPoint1)# 第五步：返回路径（封装成Route对象）return Route(path)

3. 关键步骤拆解

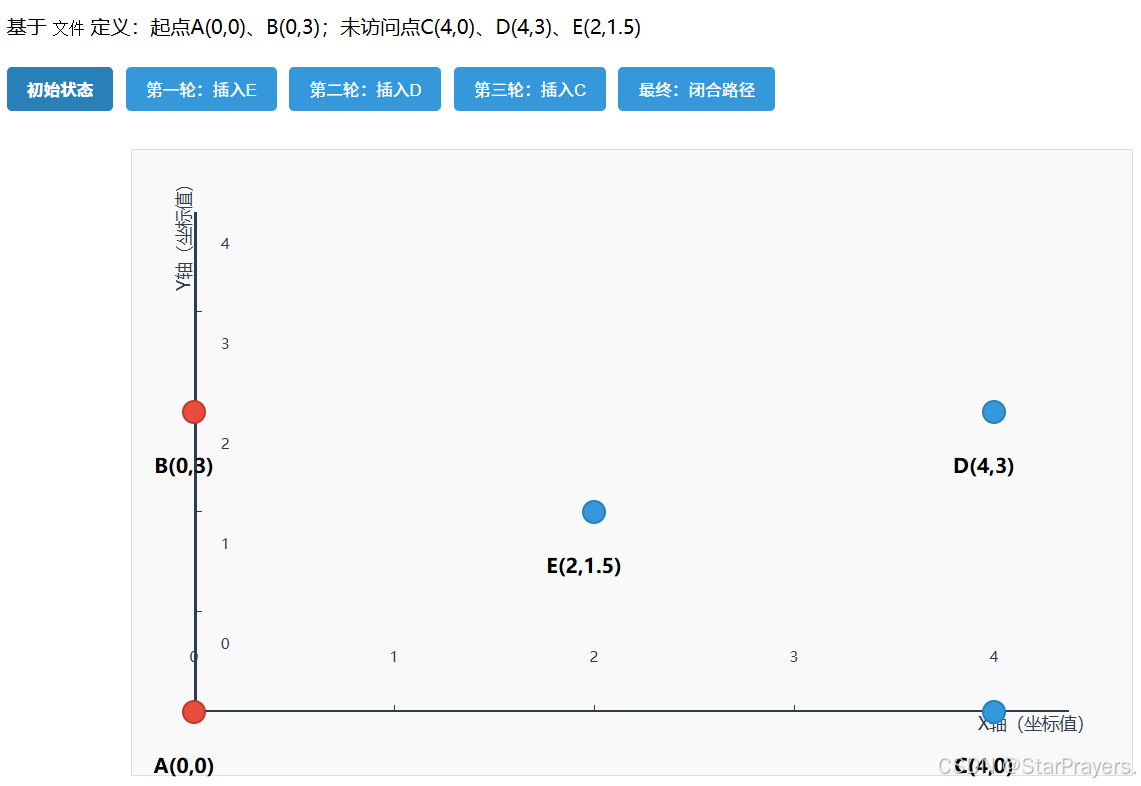
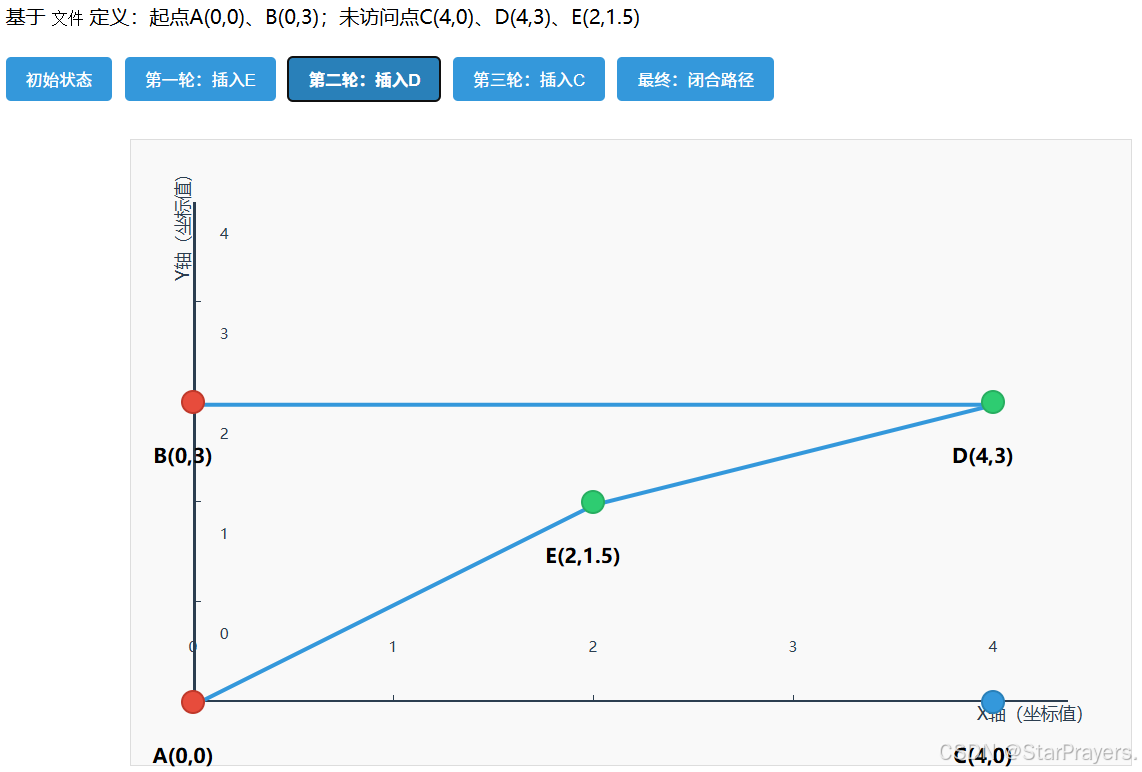
同样以 “5 点用例”、两个起点为 A (0,0) 和 B (0,3) 为例，手动走一遍流程：

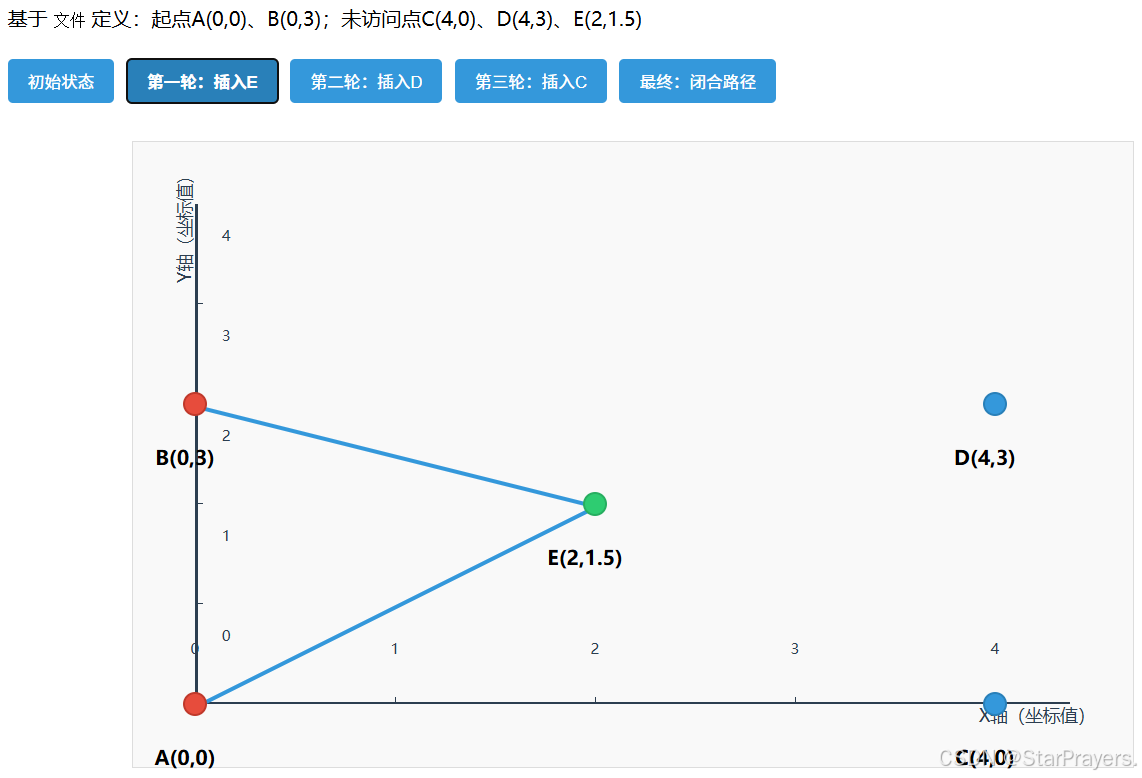
初始化：path = [A,B]，remaining = [C,D,E]；
子步骤 1：找距离路径 [A,B] 最近的点 ——E 到 A 的距离≈2.5，到 B 的距离≈2.5，是最近点（best_point=E）；
子步骤 2：找 E 的最优插入位置：
- 若插入 A 和 B 之间（位置 1）：原段 A→B 距离 = 3，插入后 A→E→B 距离≈2.5+2.5=5，增量 = 2；
- 无其他段（路径只有 A→B），因此 best_pos=1；
插入 E：path 变为 [A,B,E]，remaining = [C,D]；
下一轮循环：
- 子步骤 1：找距离路径 [A,B,E] 最近的点 ——D 到 B 的距离 = 4，到 E 的距离≈2.5，是最近点（best_point=D）；
- 子步骤 2：找 D 的最优插入位置：
  - 段 A→B：插入后 A→D→B 距离≈5+4=9，原距离 3，增量 = 6；
  - 段 B→E：插入后 B→D→E 距离 = 4+2.5=6.5，原距离 2.5，增量 = 4；
  - 段 E→A：插入后 E→D→A 距离≈2.5+5=7.5，原距离 2.5，增量 = 5；
  - 最小增量是 4，对应位置 3（B 和 E 之间）；
- 插入 D：path 变为 [A,B,D,E]，remaining = [C]；
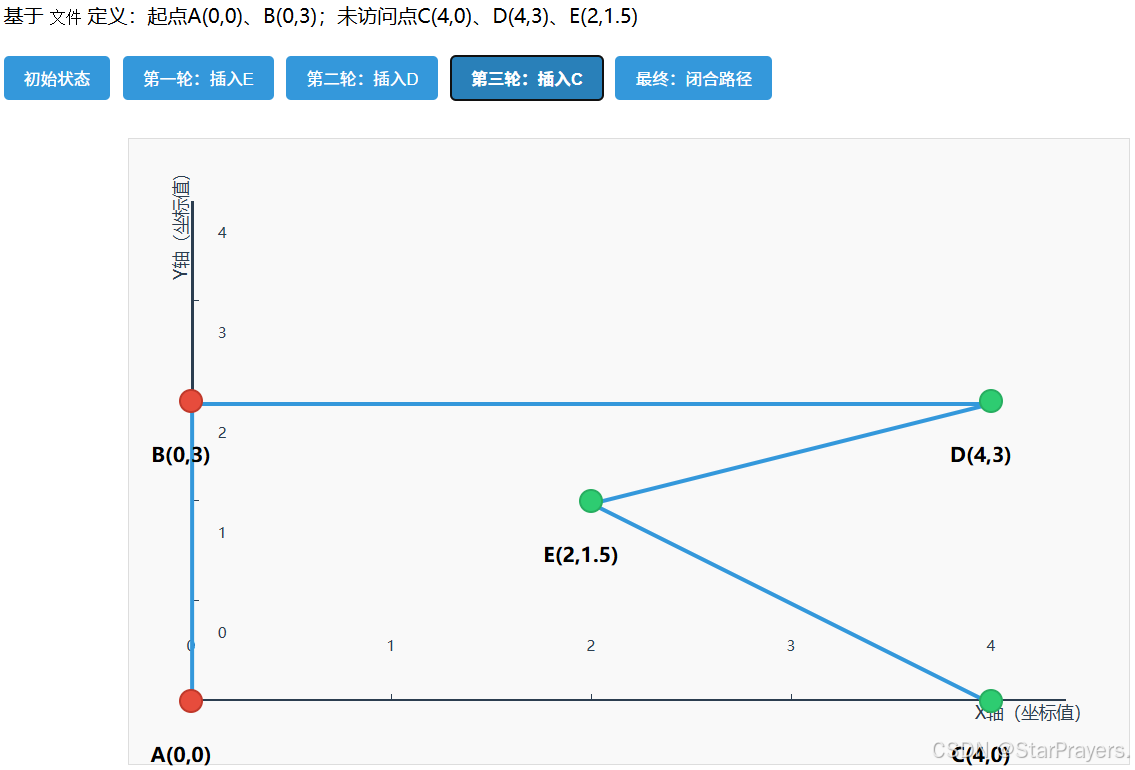
再下一轮循环：
- 子步骤 1：找距离路径 [A,B,D,E] 最近的点 ——C 到 E 的距离≈2.5，到 A 的距离 = 4，是最近点（best_point=C）；
- 子步骤 2：找 C 的最优插入位置（计算后最优位置是 5，E 和 A 之间）；
- 插入 C：path 变为 [A,B,D,E,C]，remaining 为空；
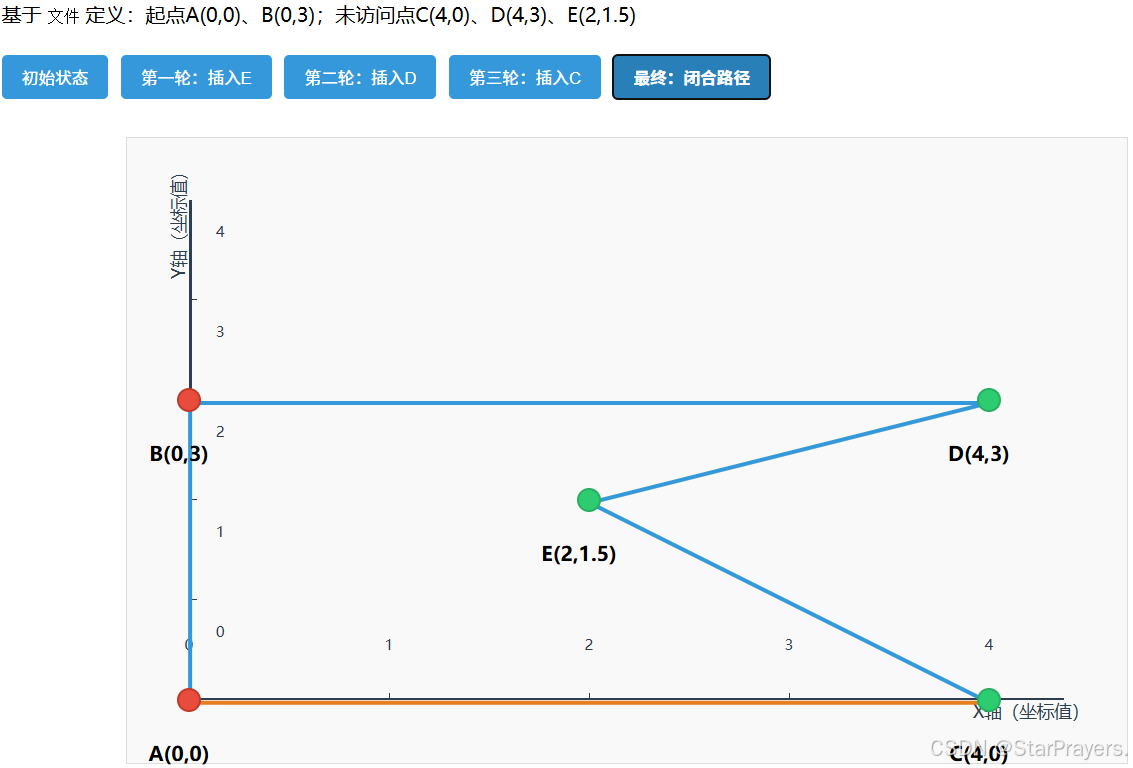
闭合路径：path 最终为 [A,B,D,E,C,A]（或等价路径），总距离≈14.898（比最近邻法更优）。

4.最近插入法（nearestInsertion）过程图

网页文件：5点用例最近插入算法流程可视化（Prayer）.html资源-CSDN下载

4. 算法特点

优点：路径总距离通常比最近邻法短（因为考虑了插入位置的优化），是更实用的近似算法；
缺点：逻辑比最近邻法复杂，计算量稍大（时间复杂度仍为 O (n²)，但常数项更大）。

heuristics.py 是整个 TSP 项目的 “算法核心”：

实现了两种贪心策略，为 TSP 提供不同精度和速度的近似解；
输出结果统一封装为 Route 对象，与 Route.py 无缝衔接，方便后续测试和可视化；
借助 @display_time 装饰器，自动统计运行时间，为后续对比算法效率提供数据支持。

若忘记算法步骤，可重点回忆：

最近邻法：“选最近点→加路径→标记已访问” 循环；
最近插入法：“选最近点→找最小增量位置→插入” 循环。两者的核心差异在于 “是否优化插入位置”，这也是最近插入法结果更优的关键。

四、heuristics.py完整代码

from Route import Route, Point
from decorator import display_time  # 导入案例要求的装饰器
import math# ---------------------- 案例必做：最近邻点法（任务1要求） ----------------------
@display_time
def nearestNeighbor(pointsL, startPoint):"""最近邻算法：从起点出发，每次选择最近未访问点（案例图2逻辑）"""# 输入验证（符合案例对函数参数的要求）if not isinstance(startPoint, Point):raise TypeError("startPoint must be a Point instance")if startPoint not in pointsL:raise ValueError("startPoint must be in pointsL")unvisited = pointsL.copy()unvisited.remove(startPoint)path = [startPoint]current = startPoint# 核心逻辑：反复选择最近未访问点while unvisited:closest = min(unvisited, key=lambda p: current.dist_to_point(p))path.append(closest)unvisited.remove(closest)current = closestpath.append(startPoint)  # 闭合路径（回到起点，符合TSP定义）return Route(path)# ---------------------- 案例必做：最近插入法（任务1要求） ----------------------
@display_time
def nearestInsertion(pointsL, startPoint1, startPoint2):"""最近插入算法：从两个起点出发，插入最近点并最小化路径增量（案例图3逻辑）"""# 输入验证（符合案例对函数参数的要求）if startPoint1 == startPoint2:raise ValueError("Start points must be different")if startPoint1 not in pointsL or startPoint2 not in pointsL:raise ValueError("Start points must be in pointsL")path = [startPoint1, startPoint2]remaining = [p for p in pointsL if p not in path]# 核心逻辑：选最近点→找最小插入位置→插入while remaining:# 步骤1：找到距离当前路径最近的点def dist_to_path(point):return min(point.dist_to_point(p) for p in path)best_point = min(remaining, key=dist_to_path)# 步骤2：找到插入后路径增量最小的位置min_increase = math.infbest_pos = 0for i in range(len(path)):a, b = path[i], path[(i + 1) % len(path)]original_dist = a.dist_to_point(b)new_dist = a.dist_to_point(best_point) + best_point.dist_to_point(b)increase = new_dist - original_distif increase < min_increase:min_increase = increasebest_pos = i + 1# 步骤3：插入点并更新剩余列表path.insert(best_pos, best_point)remaining.remove(best_point)path.append(startPoint1)  # 闭合路径return Route(path)

查看全文

http://www.dtcms.com/a/478965.html