当前位置：首页 > news >正文

深度学习周报（10.6~10.12）

news 2025/10/13 9:42:43

摘要

Abstract

1 Transformer

1.1 位置编码

1.2 总体代码梳理

1.2.1 总体架构

1.2.2 编码器与解码器

1.2.3 注意力机制与前馈神经

2 量子计算

3.1 量子门的通用性

3.2 Deutsch算法

3 总结

摘要

本周首先对位置编码进行了学习，了解了位置编码的作用与类型；其次通过代码对Transformer的架构与注意力机制等进行了梳理；最后了解了量子门的通用性，学习了Deutsch算法，了解了其思想、步骤与推广算法Deutsch-Jozsa。

Abstract

This week, I first studied positional encoding, understanding its role and types. Secondly, I reviewed the architecture of the Transformer model and the attention mechanism through code implementation. Finally, I learned about the universality of quantum gates, studied the Deutsch algorithm, and understood its core idea, procedural steps, as well as its generalized version, the Deutsch-Jozsa algorithm.

1 Transformer

1.1 位置编码

自注意力机制有一个特性，它对输入序列中所有词元进行加权求和，但本身不包含任何顺序信息。就像上周的“i need water”，将其顺序进行调整，改为“water need i”，对于自注意力机制，如果不提供额外信息，它将这两个句子视为几乎相同的，因为它只关心“i”、“need”和“water”这三个词的存在和值，而不关心它们的先后顺序。因此，我们需要一种方法将词元在序列中的位置信息注入到模型中。由此引出位置编码。

位置编码主要包括两种类型，一种是正弦式位置编码（Sinusoidal Positional Encoding），这也是原始的Attention is All You Need"(Vaswani et al., 2017) 论文中的方法，另一种是可学习位置编码（Learned Positional Embedding）。

正弦式位置编码的设计思想主要包括：第一，每个位置的编码必须唯一；第二，编码应该由位置直接计算得出，而不是需要学习的参数（不过后来也有模型使用可学习的位置编码）；第三，模型应该能够处理比训练时看到的序列更长的序列；第四编码的值应该是有界的，不能过大；第五，编码应该能让模型轻松地学习到词元之间的相对位置关系。基于此发现，正弦和余弦函数的周期性特点完美地满足了这些要求。

对于一个位于位置 $pos$ 的词元，其位置编码 $PE$ 是一个 $d_{model}$ 维的向量，这个向量的第 $i$ 个维度的值计算如下：

$PE_{\left (pos ,2i \right )}= sin\left ( \frac{pos}{10000^{2i/d_{model}}} \right )$

$PE_{\left (pos ,2i+1 \right )}= cos\left ( \frac{pos}{10000^{2i/d_{model}}} \right )$

$d_{model}$ 实际上也是原输入词向量的维度，计算出位置编码后将其加到词向量上得到最终的输入。

而现代模型（如BERT等）也会使用可学习的位置编码，因为这种方式允许模型在训练过程中自动学习和调整位置表示，而不是使用固定的、预定义的函数，更加灵活，且实现简单，性能良好。

其他的还有相对位置编码（Relative Positional Encoding），它不编码绝对位置，而是对相对距离进行建模，更加符合语言规律；旋转位置编码（Rotary Position Embedding, RoPE），它将位置信息编码为旋转矩阵，通过旋转向量引入顺序，支持长序列、外推性好，被广泛用于PaLM、 LLaMA、ChatGLM等大模型；ALiBi（Attention with Linear Biases），这种方式不显式加编码，而是在注意力分数上加一个与距离成线性的偏置，完全无需位置编码，同时支持极长上下文。

1.2 总体代码梳理

1.2.1 总体架构

输入先经过词嵌入与位置编码得到

# Transformer整体架构
class SimpleTransformer(nn.Module):def __init__(self, src_vocab_size, tgt_vocab_size, d_model=512, num_layers=6,num_heads=8, d_ff=2048, max_seq_len=100):# src_vocab_size代表源语言词汇表大小，tgt_vocab_size代表目标语言词汇表大小# d_model代表隐藏维度，num_layers代表编码器与解码器层数# num_heads代表注意力头数，d_ff代表前馈网络维度，max_seq_len表示最长处理词数super().__init__()self.d_model = d_model# 词嵌入self.src_embedding = nn.Embedding(src_vocab_size, d_model)self.tgt_embedding = nn.Embedding(tgt_vocab_size, d_model)# 位置编码self.positional_encoding = self.create_positional_encoding(max_seq_len, d_model)# 编码器层self.encoder_layers = nn.ModuleList([SimpleTransformerBlock(d_model, num_heads, d_ff, is_decoder=False)for _ in range(num_layers)])# 解码器层self.decoder_layers = nn.ModuleList([SimpleTransformerBlock(d_model, num_heads, d_ff, is_decoder=True)for _ in range(num_layers)])# 输出层self.output_layer = nn.Linear(d_model, tgt_vocab_size)# 位置编码def create_positional_encoding(self, max_len, d_model):pe = torch.zeros(max_len, d_model)   #初始化位置编码矩阵#生成位置索引，unsqueeze(1) 表示增加一个维度，变成列向量，形状 (max_len, 1)position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)   #分母项div_term = torch.exp(torch.arange(0, d_model, 2).float() *(-math.log(10000.0) / d_model))#交替使用正弦与余弦pe[:, 0::2] = torch.sin(position * div_term)pe[:, 1::2] = torch.cos(position * div_term)#增加维度pe = pe.unsqueeze(0) return pe# 掩码def create_causal_mask(self, seq_len):mask = torch.tril(torch.ones(seq_len, seq_len))  # 下三角矩阵return mask.unsqueeze(0).unsqueeze(0)  # (1, 1, seq_len, seq_len)# 前向def forward(self, src, tgt):batch_size, src_len = src.shape   #获取输入批次大小和源句长度_, tgt_len = tgt.shape   #获取目标句长度# 编码器 词嵌入+位置编码+编码器堆叠src_embedded = self.src_embedding(src) * math.sqrt(self.d_model)src_embedded = src_embedded + self.positional_encoding[:, :src_len, :]encoder_output = src_embeddedfor layer in self.encoder_layers:encoder_output = layer(encoder_output)# 解码器 词嵌入+位置编码+掩码+解码器堆叠tgt_embedded = self.tgt_embedding(tgt) * math.sqrt(self.d_model)tgt_embedded = tgt_embedded + self.positional_encoding[:, :tgt_len, :]causal_mask = self.create_causal_mask(tgt_len)decoder_output = tgt_embeddedfor layer in self.decoder_layers:decoder_output = layer(decoder_output, encoder_output, causal_mask)# 输出output = self.output_layer(decoder_output)return output

1.2.2 编码器与解码器

上一节中，编码器层和解码器层代码具体如下（包括注意力机制，前馈神经网络、残差连接、层归一化）：

# Transformer块（编码器/解码器）
class SimpleTransformerBlock(nn.Module):def __init__(self, d_model, num_heads, d_ff, is_decoder=False):super().__init__()self.is_decoder = is_decoder# 自注意力self.self_attention = SimpleMultiHeadAttention(d_model, num_heads)# 如果是解码器，添加交叉注意力if is_decoder:self.cross_attention = SimpleMultiHeadAttention(d_model, num_heads)# 前馈网络self.feed_forward = SimpleFeedForward(d_model, d_ff)# 层归一化self.norm1 = nn.LayerNorm(d_model)self.norm2 = nn.LayerNorm(d_model)if is_decoder:self.norm3 = nn.LayerNorm(d_model)def forward(self, x, encoder_output=None, mask=None):# 自注意力 + 残差连接 + 层归一化attn_output = self.self_attention(x, x, x, mask)x = self.norm1(x + attn_output)# 如果是解码器，进行交叉注意力if self.is_decoder and encoder_output is not None:cross_attn_output = self.cross_attention(x, encoder_output, encoder_output)x = self.norm2(x + cross_attn_output)ff_output = self.feed_forward(x)x = self.norm3(x + ff_output)else:# 编码器：直接前馈网络ff_output = self.feed_forward(x)x = self.norm2(x + ff_output)return x

1.2.3 注意力机制与前馈神经

上一节中，多头注意力与前馈神经网络具体代码如下：

#多头注意力
class SimpleMultiHeadAttention(nn.Module):def __init__(self, d_model, num_heads):super().__init__()self.d_model = d_modelself.num_heads = num_headsself.d_k = d_model // num_heads# 线性变换层 保持维度一致self.w_q = nn.Linear(d_model, d_model)self.w_k = nn.Linear(d_model, d_model)self.w_v = nn.Linear(d_model, d_model)self.w_o = nn.Linear(d_model, d_model)def forward(self, q, k, v, mask=None):batch_size, seq_len = q.size(0), q.size(1)# 线性变换Q = self.w_q(q)K = self.w_k(k)V = self.w_v(v)# 重塑为多头Q = Q.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)K = K.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)V = V.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)# 计算注意力分数scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)# 应用掩码if mask is not None:scores = scores.masked_fill(mask == 0, -1e9)# Softmax得到注意力权重attn_weights = torch.softmax(scores, dim=-1)# 应用注意力权重attn_output = torch.matmul(attn_weights, V)# 重塑回原始形状attn_output = attn_output.transpose(1, 2).contiguous().view(batch_size, seq_len, self.d_model)# 输出线性变换output = self.w_o(attn_output)return output# 前馈网络
class SimpleFeedForward(nn.Module):def __init__(self, d_model, d_ff):super().__init__()self.linear1 = nn.Linear(d_model, d_ff)self.linear2 = nn.Linear(d_ff, d_model)self.relu = nn.ReLU()def forward(self, x):return self.linear2(self.relu(self.linear1(x)))

2 量子计算

3.1 量子门的通用性

量子门的通用性（Universal Quantum Gates）是量子计算中的一个核心概念，指的是对一组有限的量子门进行组合，可以使其以任意精度逼近任意的幺正变换（即任意的量子操作），这与经典计算中“通用门”（如NAND门）可以构建任何布尔函数的概念类似。

简单来说，如果一个量子门集合是“通用的”，那么我们就可以用这个集合中的量子门来构造任何想要的量子算法，进行任意的量子操作。

一组基本的量子门操作也被称为一个通用量子门集（Universal Gate Set），由于量子操作必须是幺正的，并且作用在希尔伯特空间上，所以通用性也意味着，对于任意给定的幺正算符 U 和任意小的精度 $\varepsilon >0$ ，都存在一个由该门集中的门构成的量子电路，使得该电路实现的幺正变换与 U 的距离小于 $\varepsilon$ 。

p.s. 幺正（Unitary）描述的是一种保持内积不变的线性变换或矩阵，这种变换不会改变向量的长度（模）和向量之间的夹角。

常见的通用量子门集包括以下几种：

第一个就是由所有单量子比特门（例如，Hadamard门（H）、相位门（S）、π/8门（T）等）与一个两量子比特门CNOT（受控非门）构成的，这是最常用和最重要的通用门集之一，大多数量子计算架构（如超导、离子阱等）都基于这个门集来设计和编译量子程序。

第二个集合则更加具体，由H门、T门与CNOT门构成，这个集合被称为标准通用门集，广泛用于量子线路编译和容错量子计算，其中T门提供了一个不可由H和S生成的非Clifford操作，这是实现通用性的关键。

另外还有Toffoli门加上H门、CZ门加上单量子比特门以及某些三量子比特门或特殊门（如FREDKIN门）加上单量子比特门也可构成通用集。

通用性在理论上保证了量子计算机的计算能力完备性，在应用中允许通过有限的门的操作实现复杂的量子算法，降低了实现难度。但使用有限门集逼近任意门一来无可避免地会引入误差，需要进行控制；二来逼近可能需要很长的量子线路，会导致噪声和出错概率的增加。

也因此，量子编译器（如Qiskit、Cirq）的核心任务之一就是将高级量子操作分解为通用门集中的基本门序列，并尽量优化电路。

3.2 Deutsch算法

Deutsch算法是量子计算领域中的第一个重要算法，由大卫·德意志（David Deutsch）于1985年提出。这个算法虽然简单，但具有里程碑意义，因为它首次展示了量子计算机可以比经典计算机更快地解决某一类问题。

Deutsch算法解决的是一个非常简单的“函数性质判断”问题，如下：

给定一个黑箱函数 $f:\left \{ 0,1 \right \}\rightarrow \left \{ 0,1 \right \}$ ，判断它是常数函数还是平衡函数。在经典计算中，你需要查询两次函数才能确定结果。但在量子计算中，只需一次查询就可以以100%的概率判断出函数类型。这表现了量子并行性和干涉效应的威力。

p.s. 常数函数（constant）指的是其所有输出相同，平衡函数（balanced）指的是其所有输出占比一致。按上述黑箱函数，输出有四种可能，f(0)和 f(1) 的值可能为00，11，01，10，前两种为常数函数，后两种为平衡函数。

Deutsch算法大致是使用两个量子比特以及一个称为 Oracle（黑箱）的量子门 $U_{f}$ 来实现函数 $f$ ，并定义 Oracle如下：

$U_{f}|x\rangle|y\rangle = |x\rangle|y \oplus f\left ( x \right )\rangle$

具体步骤如下：

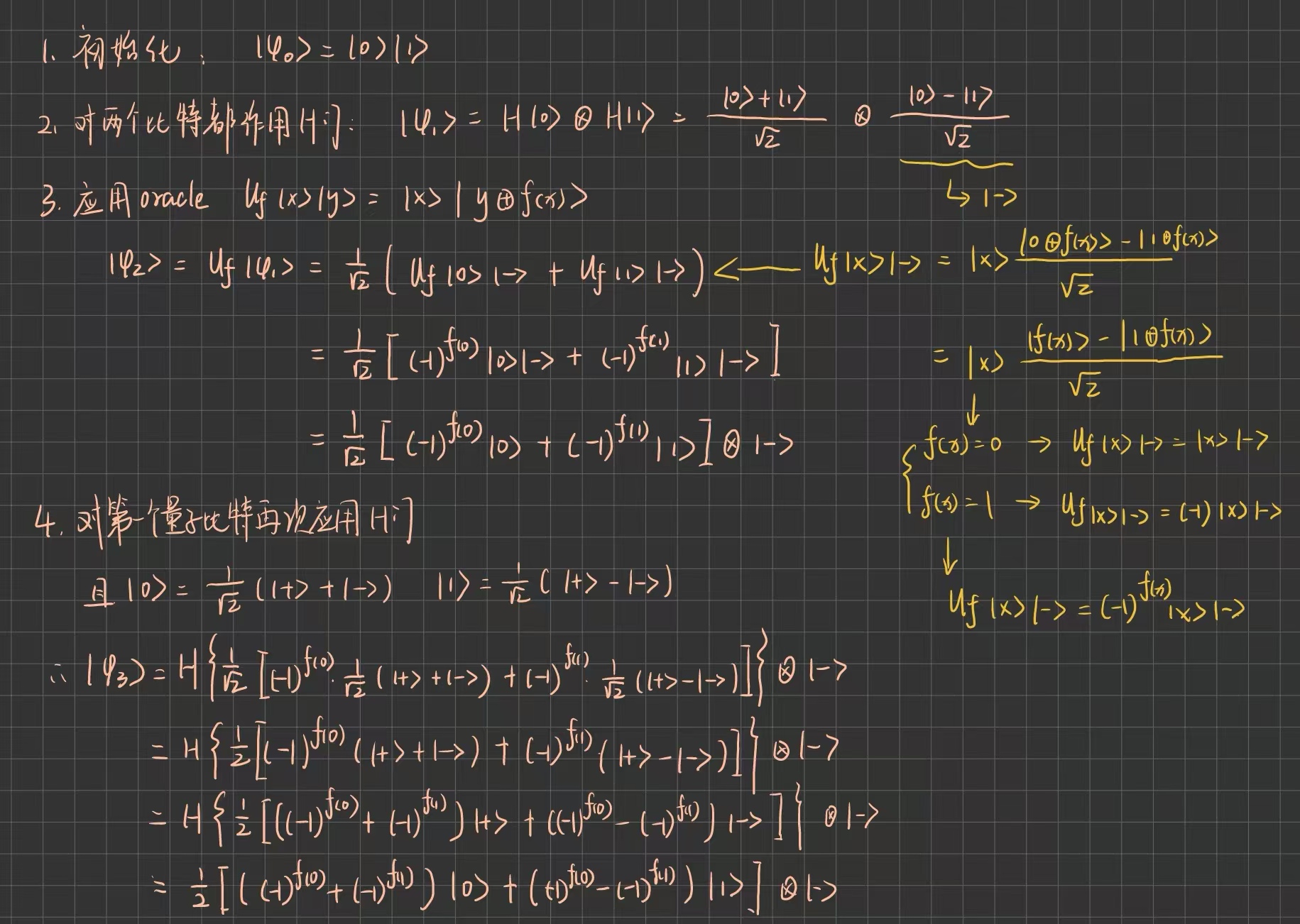
假设第一部分为 $|\phi \rangle$ 。若函数为常数函数，则：

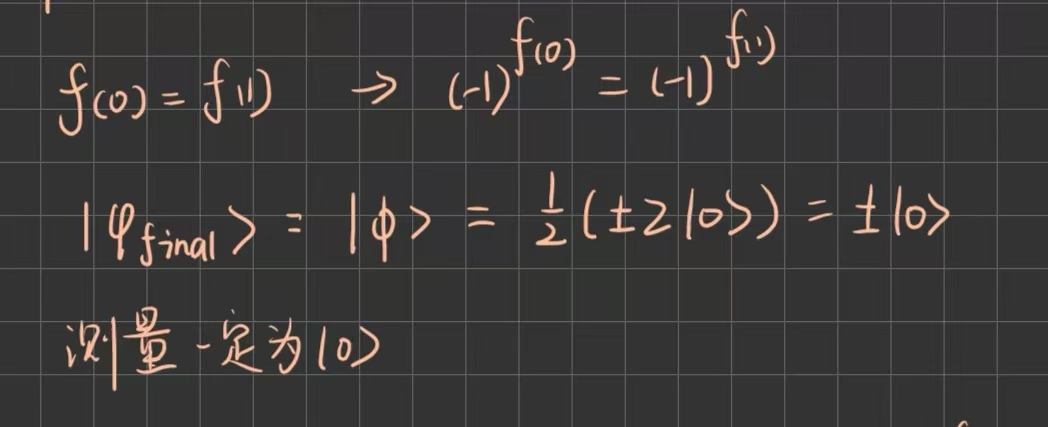
若为平衡函数，则：

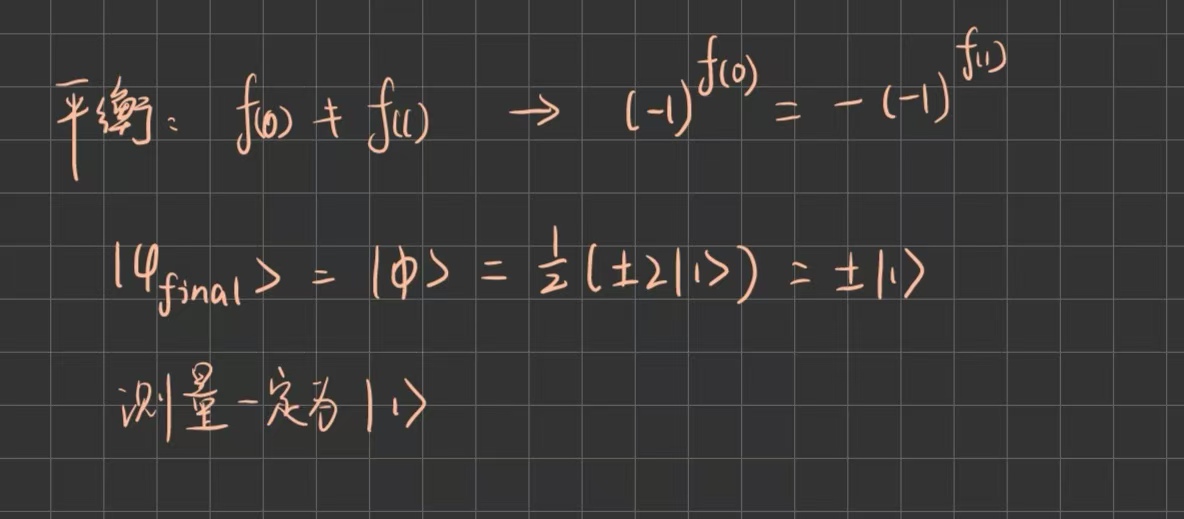
Deutsch算法首次展示了量子加速，虽然只是从 2次到1次查询，但它证明了量子计算机可以在某些任务上超越经典计算机，同时它引入了Oracle 模型，为后续算法（如 Deutsch-Jozsa、Simon、Grover、Shor等）奠定了基础。

Deutsch-Jozsa算法是对原始 Deutsch算法的推广，由David Deutsch和Richard Jozsa于1992年提出。如果说Deutsch算法只是从2次查询优化到了1次，那么它就是首次清晰地展示了量子计算机相对于经典确定性算法的指数级加速潜力。

同样还是给定一个黑箱函数，判断它是常数函数还是平衡函数。其不同的地方在于给定的黑箱函数如下： $f:\left \{ 0,1 \right \}^{n}\rightarrow \left \{ 0,1 \right \}$ 。对于经典确定性算法，其最坏的情况下需要 $2^{n-1}+1$ 次查询，而Deutsch-Jozsa算法只需要一次。它的步骤与Deutsch大致相似，区别在于它前n个比特全为 $|0\rangle$ ，只有最后一个辅助比特为 $|1\rangle$ 。