当前位置：首页 > news >正文

AprioriFP-Growth算法详解

news 2025/10/13 9:38:07

创作不易，请一键三连哦～

再次感叹人类智慧，这种经典算法实在是太美妙了

Apriori算法

Apriori算法的执行流程主要包含两个步骤：

频繁项集生成（Frequent Itemset Generation）: 找出满足最小支持度阈值的所有频繁项集。
关联规则生成（Association Rule Generation）: 从频繁项集中生成高置信度的关联规则。

Step1: 频繁项集生成

扫描数据集，找出所有单一项的支持度，并筛选出满足最小支持度的项。
使用满足最小支持度的项生成新的候选项集。

计算新生成的候选项集的支持度，并再次筛选。

交易ID	商品列表
T1	{牛奶, 面包, 黄油, 鸡蛋}
T2	{牛奶, 面包, 饼干, 可乐}
T3	{牛奶, 黄油, 鸡蛋}
T4	{面包, 黄油, 苹果}
T5	{牛奶, 面包, 黄油, 苹果}
T6	{牛奶, 面包, 鸡蛋, 苹果}
T7	{牛奶, 饼干, 可乐}
T8	{牛奶, 面包, 黄油}
T9	{面包, 黄油, 鸡蛋}
T10	{牛奶, 面包, 可乐}

设定最小支持度（min_sup）= 0.3（即至少出现3次）最小置信度（min_conf）= 0.6

1️⃣ .单一项支持度

商品	出现次数	支持度	是否保留
牛奶	8	0.8	✅
面包	8	0.8	✅
黄油	6	0.6	✅
鸡蛋	4	0.4	✅
苹果	3	0.3	✅
饼干	2	0.2	❌
可乐	3	0.3	✅

L1: {牛奶}, {面包}, {黄油}, {鸡蛋}, {苹果}, {可乐}

2️⃣.使用L1生成候选L2项集（L2不会有饼干）

项集	出现次数	支持度
{牛奶, 面包}	6	0.6 ✅
{牛奶, 黄油}	4	0.4 ✅
{牛奶, 鸡蛋}	3	0.3 ✅
{牛奶, 苹果}	2	0.2 ❌
{牛奶, 可乐}	3	0.3 ✅
{面包, 黄油}	5	0.5 ✅
{面包, 鸡蛋}	3	0.3 ✅
{面包, 苹果}	3	0.3 ✅
{面包, 可乐}	3	0.2 ❌
{黄油, 鸡蛋}	3	0.3 ✅
{黄油, 苹果}	2	0.2 ❌
{鸡蛋, 苹果}	1	0.1 ❌
{苹果, 可乐}	0	0.0 ❌

L2:候选2项集
{牛奶, 面包}, {牛奶, 黄油}, {牛奶, 鸡蛋}, {牛奶, 可乐}, {面包, 黄油}, {面包, 鸡蛋}, {面包, 苹果},{黄油, 鸡蛋}

3️⃣.使用L2生成候选L3项集

代码里是用

candidates = {itemset1 | itemset2 for itemset1 in prev_frequent_itemsets for itemset2 in prev_frequent_itemsets if len(itemset1 | itemset2) == len(itemset1) + 1}

但其实也可以剪枝，比如{牛奶, 面包, 可乐} ，可以通过{牛奶，面包}和{牛奶，可乐}得到，但是{面包，可乐}支持度仅为0.2，那么其实这个项集可以不用再计算了

项集	出现次数	支持度
{牛奶, 面包, 黄油}	3	0.3✅
{牛奶, 面包, 鸡蛋}	2	0.2 ❌
{面包, 黄油, 鸡蛋}	2	0.2 ❌
{牛奶, 面包, 可乐}	2	0.2 ❌
{'苹果', '面包', '黄油'}	2	0.2❌
{'鸡蛋', '苹果', '面包'}	1	0.1❌
{'苹果', '面包', '牛奶'}	2	0.2❌
{'可乐', '鸡蛋', '牛奶'}	0	0❌
{牛奶，鸡蛋，黄油}	2	0.2❌
{'可乐', '牛奶', '黄油'}	0	0❌

4️⃣.无法生成更大的频繁项集—>结束

阶段	频繁项集
L1	牛奶, 面包, 黄油, 鸡蛋, 苹果, 可乐
L2	牛奶-面包, 牛奶-黄油, 牛奶-鸡蛋, 牛奶-可乐, 面包-黄油, 面包-鸡蛋, 面包-苹果, 黄油-鸡蛋
L3	牛奶-面包-黄油

Step2: 关联规则生成

对于每一个频繁项集，生成所有可能的非空子集。
对每一条生成的规则 ( A \Rightarrow B )，计算其置信度。
如果规则的置信度满足最小置信度要求，则该规则为有效关联规则。

1️⃣.对于牛奶-面包-黄油

规则	置信度计算	结果
牛奶, 面包 → 黄油	0.3 / support（牛奶，面包）0.6= 0.5	❌
牛奶, 黄油 → 面包	0.3 / support（牛奶，黄油）0.4 = 0.75	✅
面包, 黄油 → 牛奶	0.3 / 0.5 = 0.6	✅
牛奶 → 面包, 黄油	0.3 / 0.8 <0.6	❌
面包 → 牛奶, 黄油	0.3 / 0.8 <0.6	❌
黄油 → 牛奶, 面包	0.3 / 0.6 = 0.5	❌

2️⃣.对于一系列L2候选集相同操作

Step3: 代码测试

from itertools import chain, combinations
# 生成候选项集的所有非空子集
def powerset(s):return chain.from_iterable(combinations(s, r) for r in range(1, len(s)))# 计算支持度
def calculate_support(itemset, transactions):return sum(1 for transaction in transactions if itemset.issubset(transaction)) / len(transactions)
def apriori(transactions, min_support, min_confidence):# 初始化频繁项集和关联规则列表frequent_itemsets = []association_rules = []# 第一步：找出单项频繁项集singletons = {frozenset([item]) for transaction in transactions for item in transaction}singletons = {itemset for itemset in singletons if calculate_support(itemset, transactions) >= min_support}frequent_itemsets.extend(singletons)# 迭代找出所有其他频繁项集prev_frequent_itemsets = singletonswhile prev_frequent_itemsets:# 生成新的候选项集## 不剪枝# candidates = {itemset1 | itemset2 for itemset1 in prev_frequent_itemsets for itemset2 in prev_frequent_itemsets if len(itemset1 | itemset2) == len(itemset1) + 1}## Join + Prune剪枝candidates = set()for itemset1 in prev_frequent_itemsets:for itemset2 in prev_frequent_itemsets:union_set = itemset1 | itemset2if len(union_set) == len(itemset1) + 1:# 🔍 检查所有 (k-1)-子集是否都频繁（即在 L_{k-1} 中）all_subsets_frequent = all(frozenset(subset) in prev_frequent_itemsetsfor subset in map(set, combinations(union_set, len(union_set) - 1)))if all_subsets_frequent:candidates.add(union_set)print(list((calculate_support(itemset, transactions),itemset) for itemset in candidates))# 计算支持度并筛选new_frequent_itemsets = {itemset for itemset in candidates if calculate_support(itemset, transactions) >= min_support}frequent_itemsets.extend(new_frequent_itemsets)# 生成关联规则for itemset in new_frequent_itemsets:for subset in powerset(itemset):subset = frozenset(subset)diff = itemset - subsetprint((subset,diff))if diff:confidence = calculate_support(itemset, transactions) / calculate_support(subset, transactions)if confidence >= min_confidence:association_rules.append((subset, diff, confidence))prev_frequent_itemsets = new_frequent_itemsetsreturn frequent_itemsets, association_rules
transactions = [{'牛奶', '面包', '黄油', '鸡蛋'},{'牛奶', '面包', '饼干', '可乐'},{'牛奶', '黄油', '鸡蛋'},{'面包', '黄油', '苹果'},{'牛奶', '面包', '黄油', '苹果'},{'牛奶', '面包', '鸡蛋', '苹果'},{'牛奶', '饼干', '可乐'},{'牛奶', '面包', '黄油'},{'面包', '黄油', '鸡蛋'},{'牛奶', '面包', '可乐'}
]
min_support = 0.3
min_confidence = 0.6frequent_itemsets, association_rules = apriori(transactions, min_support, min_confidence)print("频繁项集：", frequent_itemsets)
print("关联规则：", association_rules)

FP-Growth：挖掘频繁项集

和Apriori算法相比，FP-growth算法只需要对数据库进行两次遍历，从而高效发现频繁项集。

FP树（Frequent Pattern Tree）：一种紧凑数据结构来存储频繁项集信息

每个节点表示一个项，每个路径表示一个事务

Step1: 项头表的建立

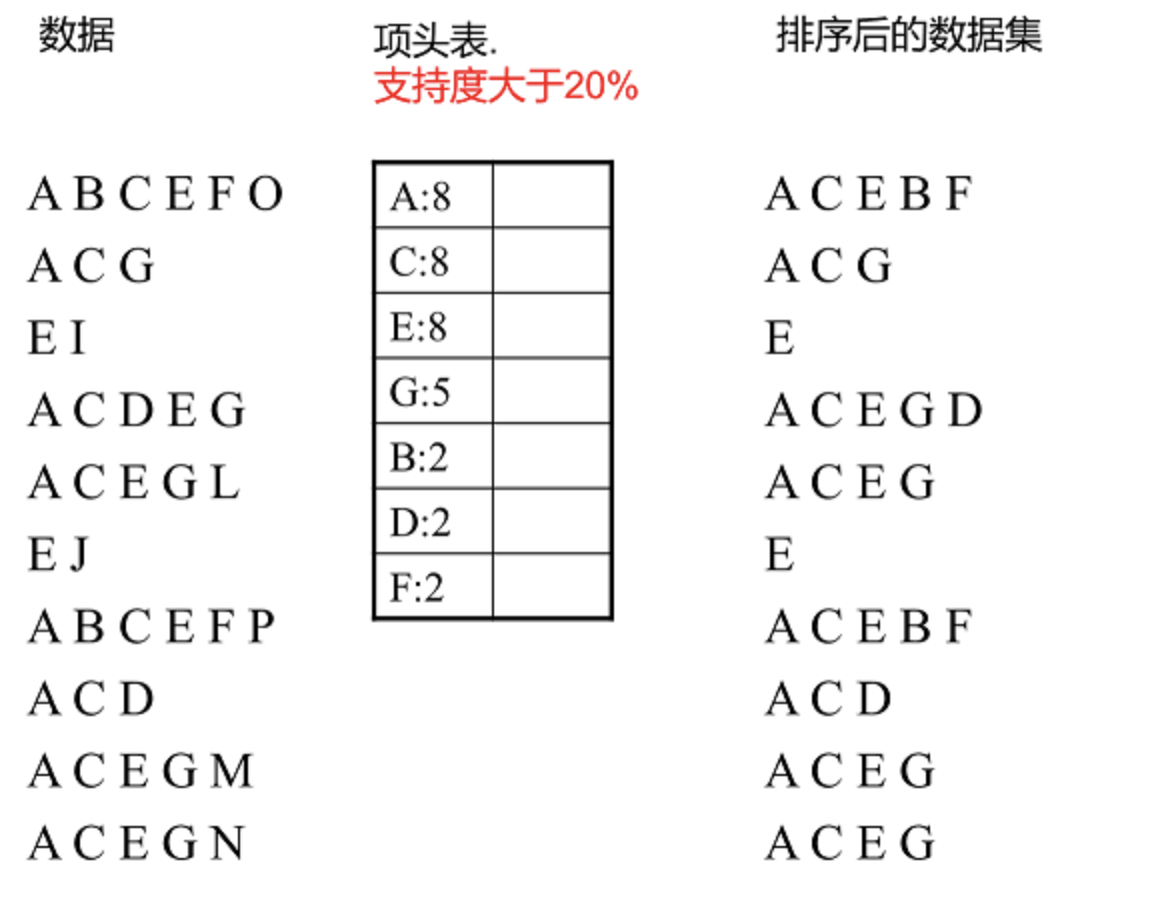
1️⃣.第一次扫描扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列（和Apriori类似）

2️⃣.第二次扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列

比如数据项ABCEFO，里面O是非频繁1项集，因此被剔除，只剩下了ABCEF。按照支持度的顺序排序，它变成了ACEBF

3️⃣.读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成

Step2: FP树的建立

1️⃣.读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成

插入第一条数据ACEBF

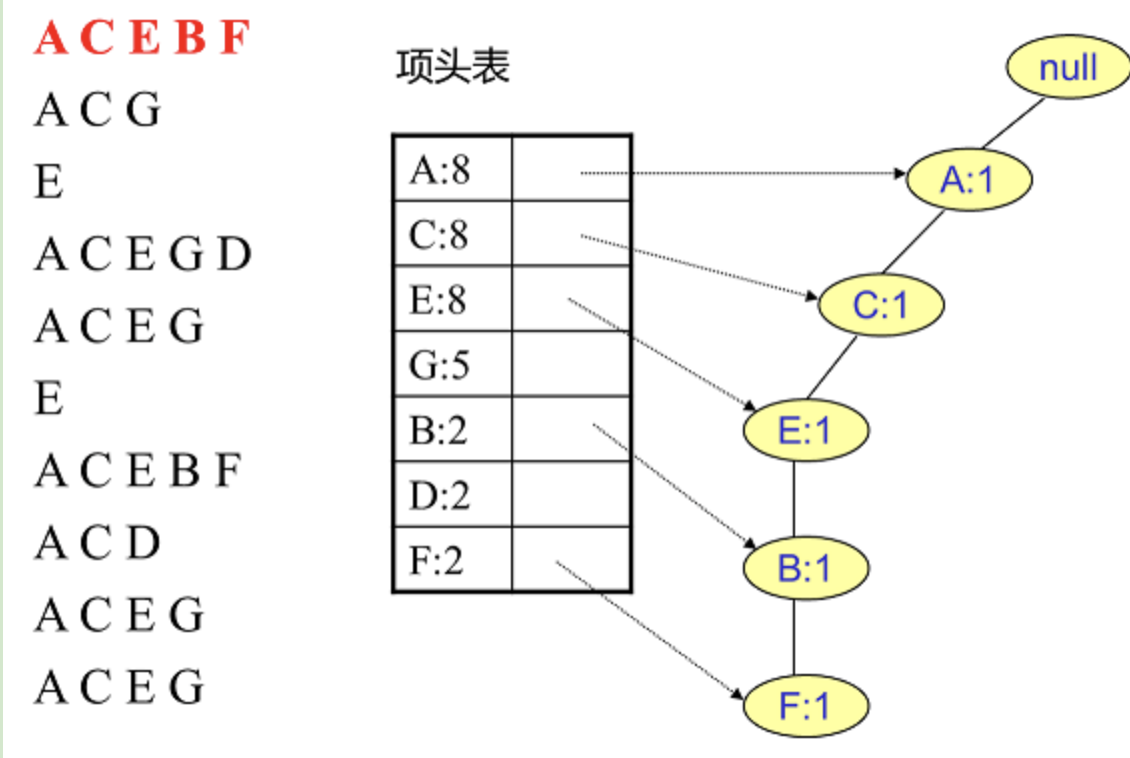
插入数据ACG，增加一个新节点G，计数为1，A和C的计数加1成为2

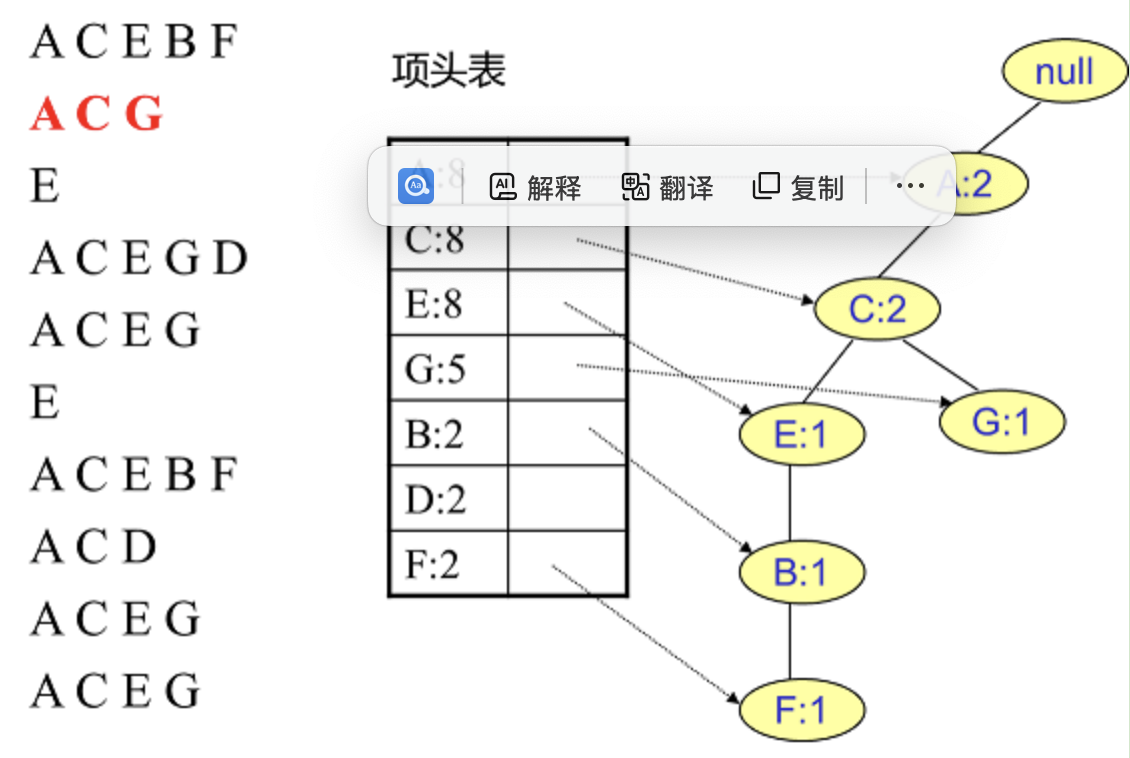
插入其他数据

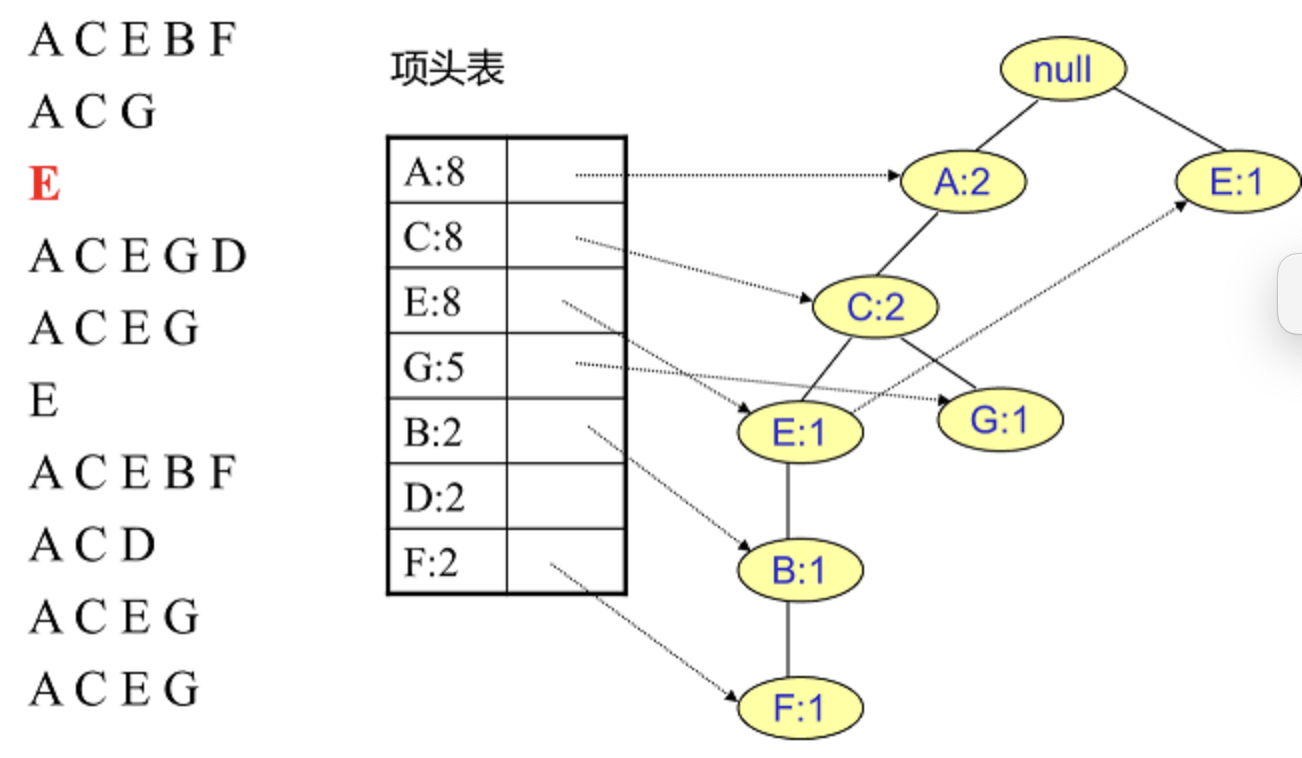
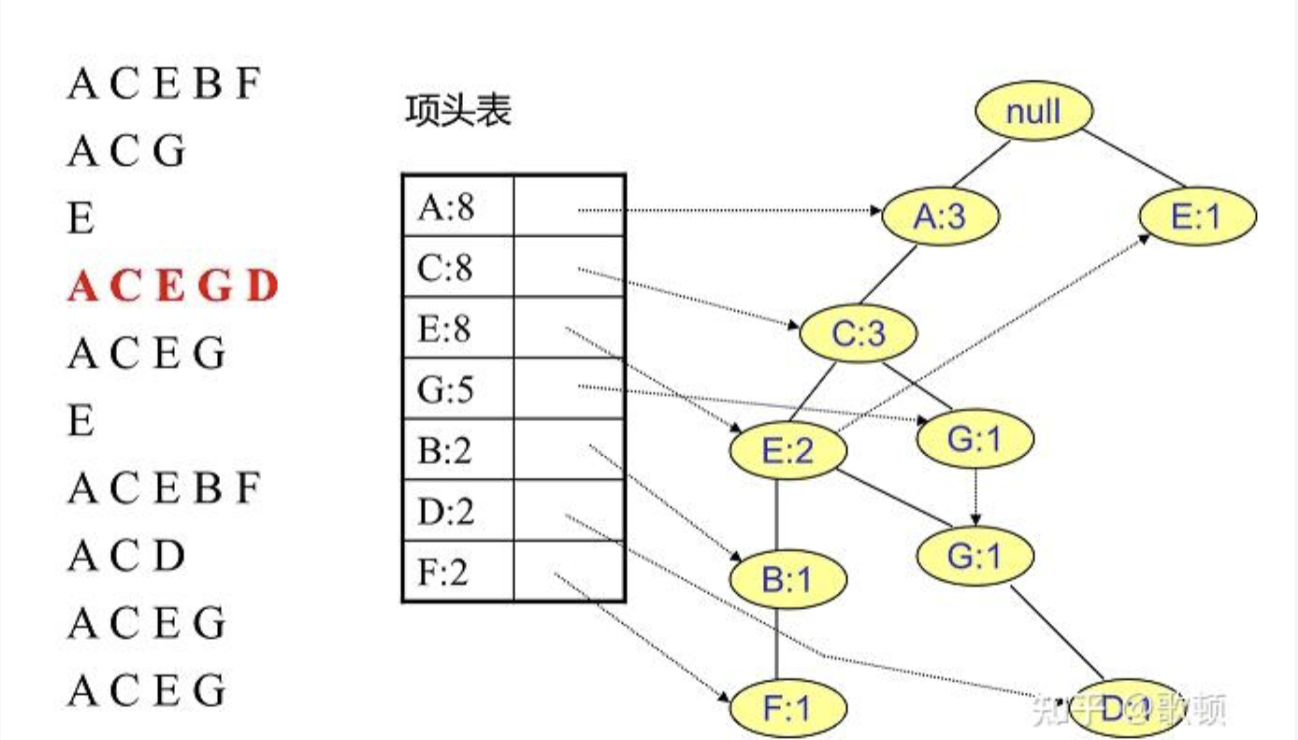
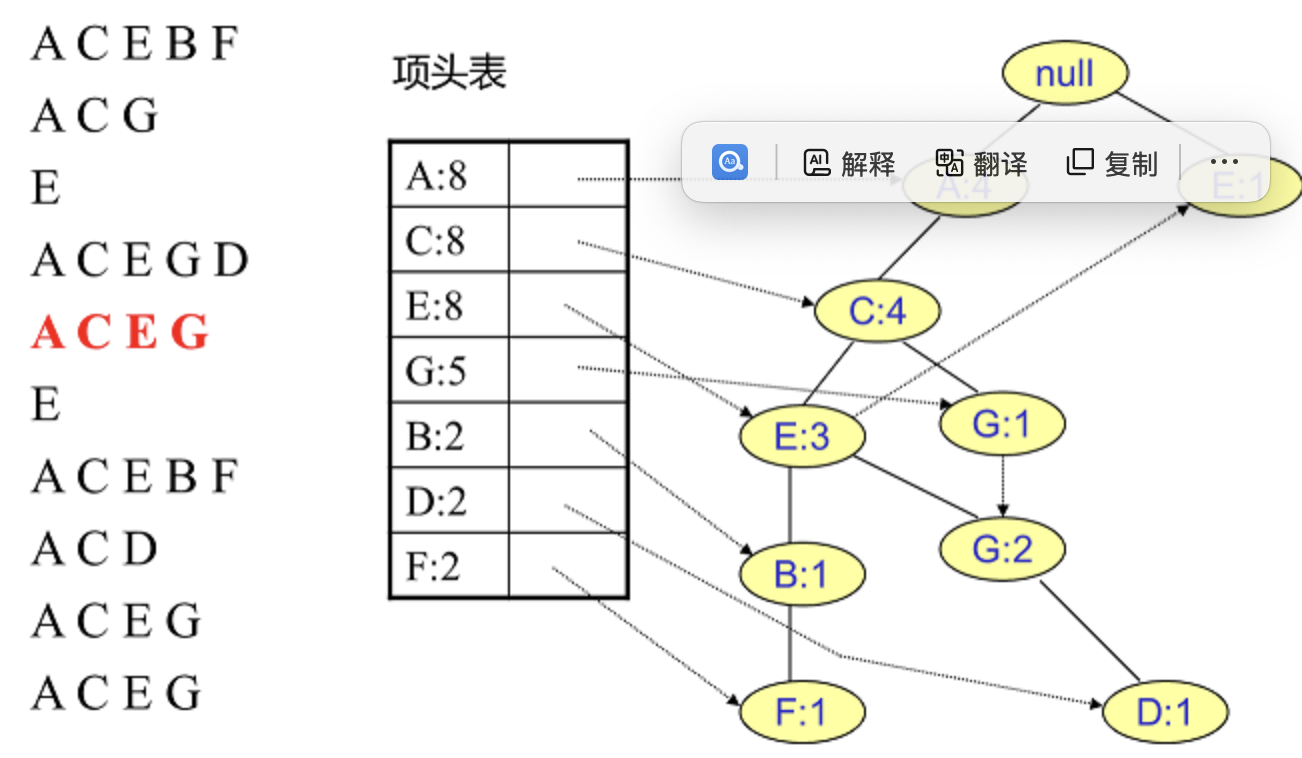
...略

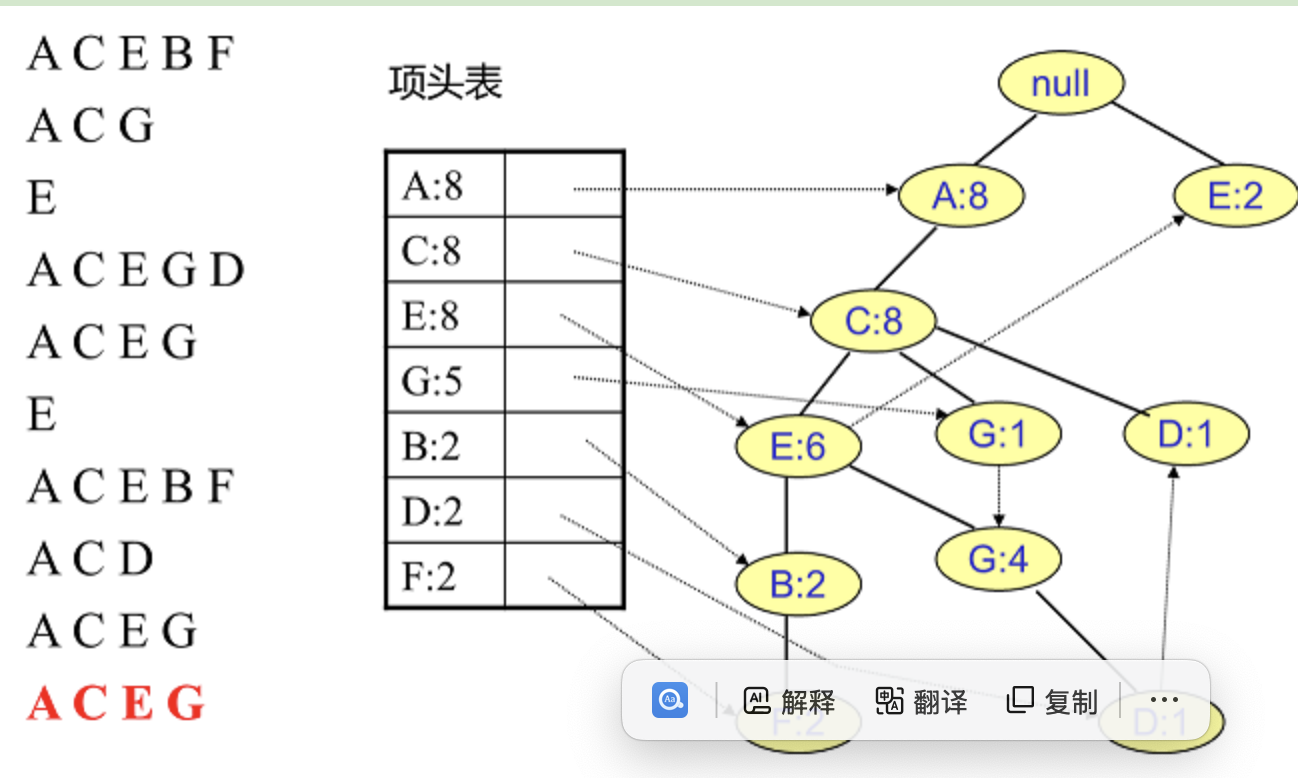
Step3: 挖掘频繁项集

1️⃣.从项头表的底部项依次向上挖掘。对于项头表对应于FP树的每一项，我们要找到它的条件模式基。所谓条件模式基是以我们要挖掘的节点作为叶子节点所对应的FP子树。得到这个FP子树，我们将子树中每个节点的的计数设置为叶子节点的计数，并删除计数低于支持度的节点。从这个条件模式基，我们就可以递归挖掘得到频繁项集了。

F条件模式基:只有一个节点，一条候选路径ACEBF
- 将所有的祖先节点计数设置为叶子节点的计数，即FP子树变成{A:2,C:2,E:2,B:2, F:2}
- 通过它，我们很容易得到F的频繁2项集为{A:2,F:2}, {C:2,F:2}, {E:2,F:2}, {B:2,F:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,F:2}，{A:2,E:2,F:2},...还有一些频繁三项集，就不写了。当然一直递归下去，最大的频繁项集为频繁5项集，为{A:2,C:2,E:2,B:2,F:2}

D条件模式基：两个节点
- 所有的祖先节点计数设置为叶子节点的计数，即变成{A:2, C:2,E:1 G:1,D:1, D:1}此时E节点和G节点由于在条件模式基里面的支持度低于阈值，被我们删除，最终在去除低支持度节点并不包括叶子节点后D的条件模式基为{A:2, C:2}
- 得到D的频繁2项集为{A:2,D:2}, {C:2,D:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,D:2}。D对应的最大的频繁项集为频繁3项集

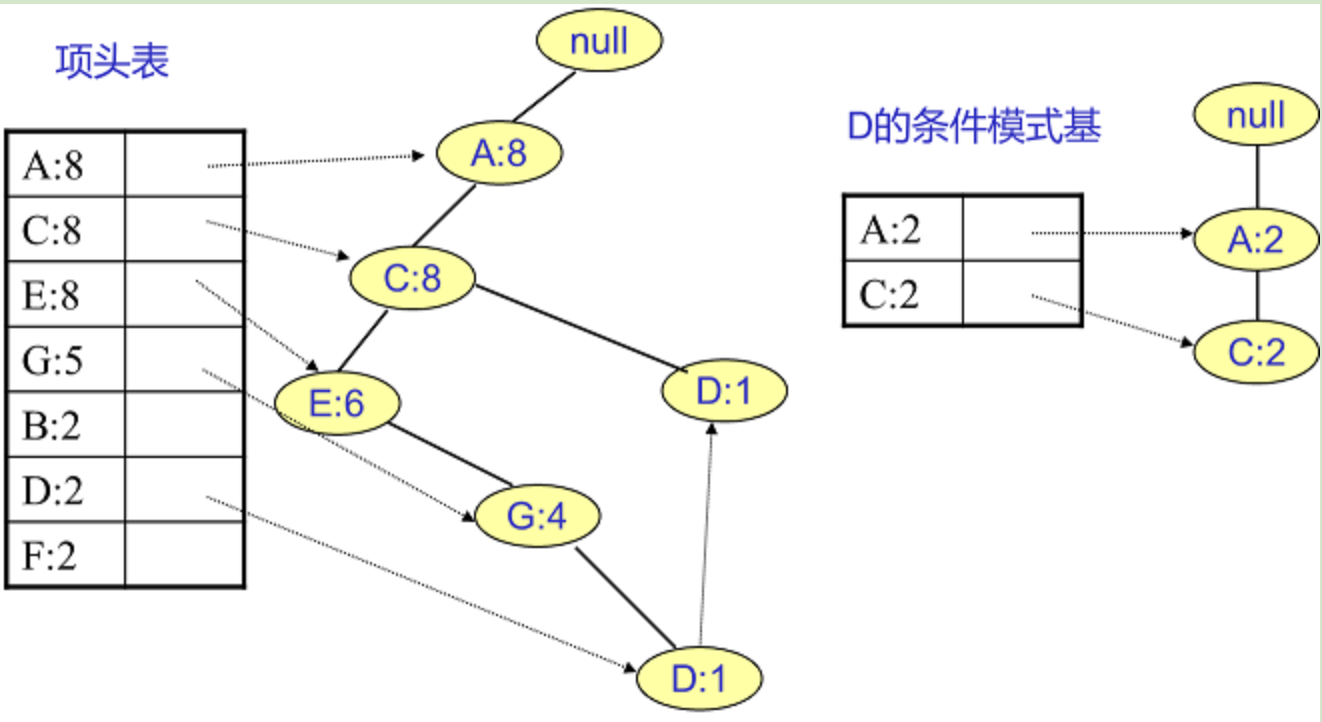
B条件模式基
- 最大频繁项集为频繁4项集{A:2, C:2, E:2,B:2}

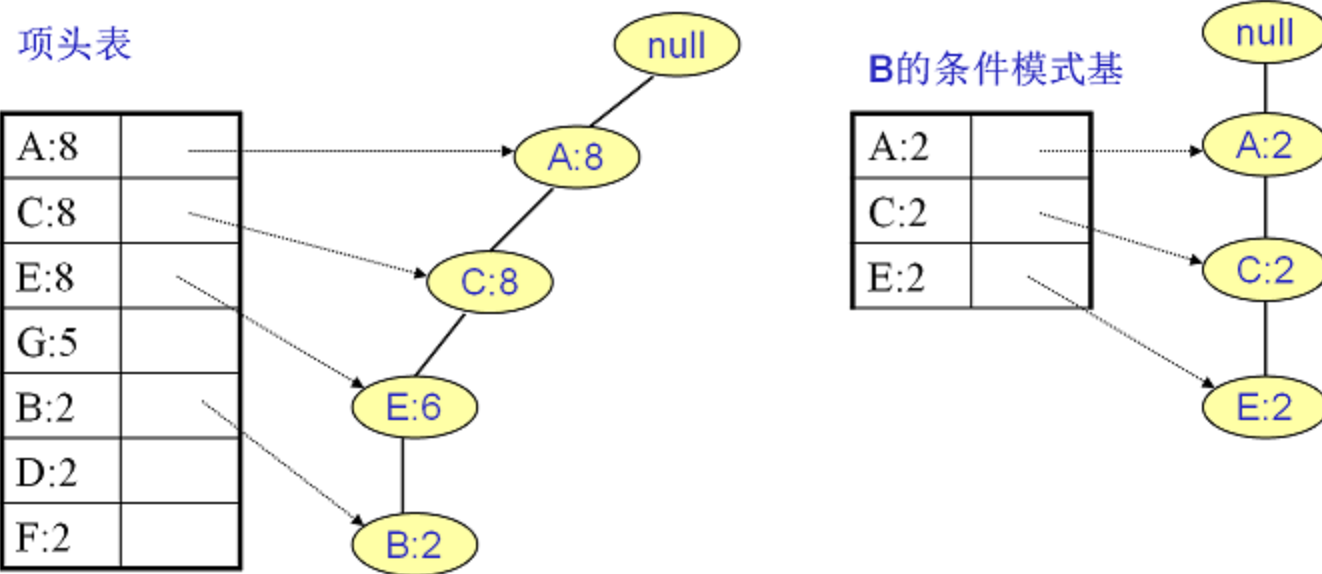
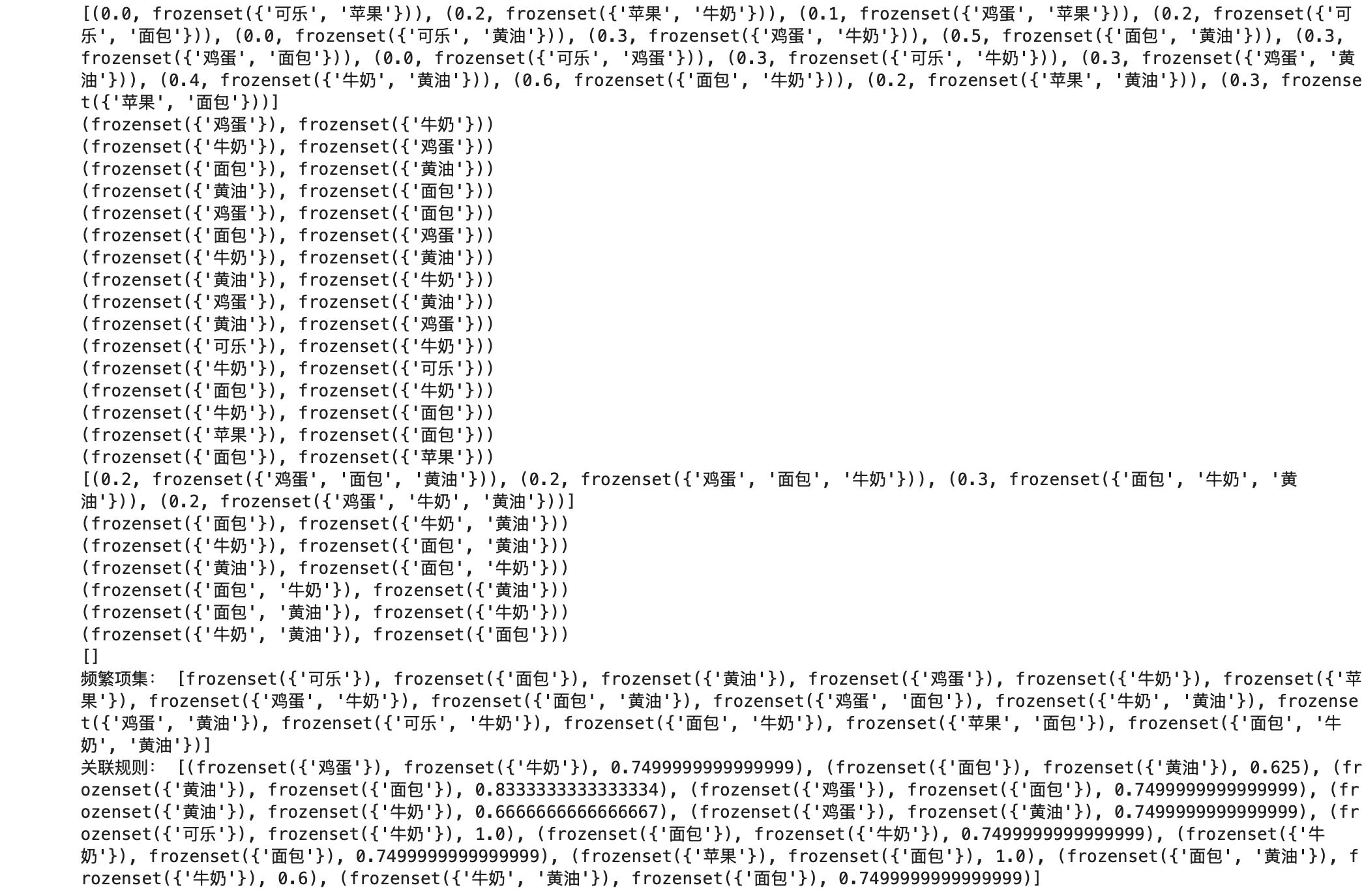
G条件模式基:最大是频繁4项集{A:5,C:5,E:4,G:5}

{A:8,C:8,G:1}and{A:8,C:8,E:6,G:4}->{A:1,C:1,G:1}+{A:4,C:4,E:4,G:4}->{A:5,C:5,E:4,G:5}
E：频繁3项集{A:6, C:6, E:6}
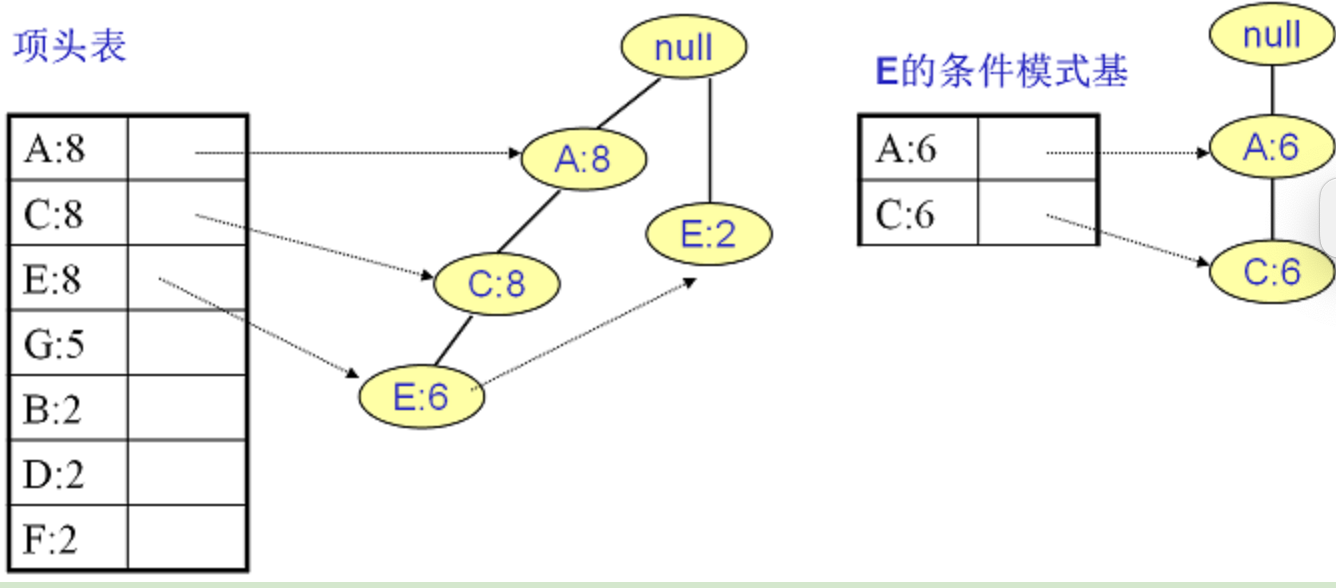
C：频繁2项集{A:8, C:8}
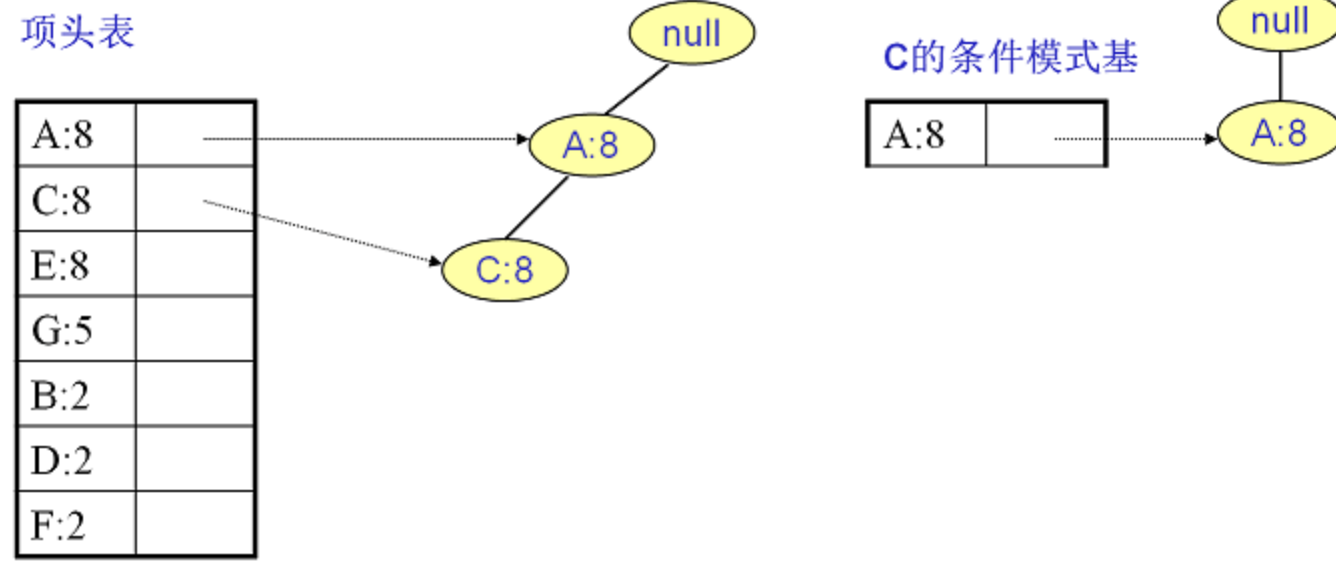
A，条件模式基为空。如果我们只是要最大的频繁K项集，从上面的分析可以看到，最大的频繁项集为5项集。包括{A:2, C:2, E:2,B:2,F:2}