当前位置：首页 > news >正文

机器学习-推荐系统（上）

news 2025/10/13 8:39:17

推荐系统：

推荐系统是日常生活中很常见的一种算法，比如购物软件中主界面上展示的商品、影视软件中首页展示的视频等，下面以电影评分为例，介绍推荐系统的建模过程。

首先，设用户数为 $n_{u}$ ，电影数为 $n_{i}$ 。显然，在收集的数据中有一些电影可能并没有被所有用户观看过，因此以二元变量 $r(i,j)$ 来表示：用户j是否有对电影i进行评分，有则为1，反之为0。而对于已经被评分的电影， $y^{(i,j)}$ 表示评分分数。

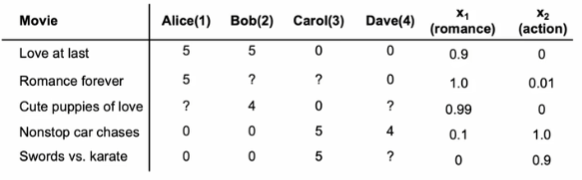
根据上述变量假设，若我们目前已知电影的特征信息，即可知每部电影对应的特征向量 $x^{(i)}$ ，特征数为n，那么对于预测每一个用户对电影的评分而言，我们可以类似线性回归进行建模，预测评分可表示为：

$f=w^{(j)}\cdot x^{(i)}+b^{(j)}$

因此对应的单个用户j的成本函数表示为：

$J=\frac{1}{2m^{(j)}}\sum_{r(i,j)=1}^{}(w^{(j)}\cdot x^{(i)}+b^{(j)}-y^{(i,j)})^{2}+\frac{\lambda }{2m^{(j)}}\sum (w_{k}^{(j)})^{2}$

其中， $m^{(j)}$ 表示对于用户j总共评价了的电影数量，而实际上这个数值是一个常数，可以移去。那么，对于所有的用户而言，整体的成本函数则为：

$J\begin{pmatrix} w^{1},w^{2}...w^{n_{u}}\\ b^{1},b^{2}...b^{n_{u}} \end{pmatrix}=\\ \sum_{j=1}^{n_{u}}[\frac{1}{2}\sum_{r(i,j)=1}^{}(w^{(j)}\cdot x^{(i)}+b^{(j)}-y^{(i,j)})^{2}+\frac{\lambda }{2}\sum (w_{k}^{(j)})^{2}]$

不过，上述的所有推导都建立在已知电影特征信息的情况下，如果以特征信息为未知量时，同上可以推导出对于每一个电影可能的特征向量，对应的成本函数为：

$J=\frac{1}{2}\sum_{r(i,j)=1}^{}(w^{(j)}\cdot x^{(i)}+b^{(j)}-y^{(i,j)})^{2}+\frac{\lambda }{2}\sum (x^{(i)})^{2}$

而对于所有的电影而言，总体的成本函数为：

$J(x^{1},x^{2}...x^{n_{i}})=\sum_{i=1}^{n_{i}}[\frac{1}{2}\sum_{r(i,j)=1}^{}(w^{(j)}\cdot x^{(i)}+b^{(j)}-y^{(i,j)})^{2}+\frac{\lambda }{2}\sum (x_{k}^{(i)})^{2}]$

协同过滤算法：

实际上，上述的三个参数 $w,b,x$ 都是未知量，因此引入协同过滤算法，则三个参数下的成本函数可以表示为：

$J(w,b,x)=\\ \frac{1}{2}\sum_{r(i,j)=1}^{}(w^{(j)}\cdot x^{(i)}+b^{(j)}-y^{(i,j)})^{2}+\frac{\lambda }{2}\sum_{j=1}^{n_{u}}\sum (w_{k}^{(j)})^{2}+\frac{\lambda }{2}\sum_{i=1}^{n_{i}}\sum (x_{k}^{(i)})^{2}$

同样类似与线性回归，梯度下降对应表达式为：

$\left\{\begin{matrix} w_{i}^{j}=w_{i}^{j}-\alpha \frac{\partial J(w,b,x)}{\partial w_{i}^{j}}\\ b^{j} = b^{j}-\alpha \frac{\partial J(w,b,x)}{\partial b^{j}} \\ x_{k}^{(i)}=x_{k}^{(i)}-\alpha \frac{\partial J(w,b,x)}{\partial x_{k}^{(i)}} \end{matrix}\right.$

之所以称之为协同过滤算法，就是因为这样建立的模型可以通过协同收集用户已经评分的数据，用于后续预测未来用户的评分行为。

二元标签：

实际情况中，除了评分之外，还有另一种更常见的二元标签，通过0-1二元变量来表示用户是否喜欢/购买/停留了解/点击某项目。对于二元标签的情况，它的建模过程类似于由线性回归转变到逻辑回归的过程。所以，此时预测得到的y表达式为：

$y^{(i,j)}=g(w\cdot x+b)$

其中：

$g(z)=\frac{1}{1+e^{-z}}$

与逻辑回归一样，此时我们不再采用均方误差作为损失，对于单个样本，其损失函数为：

$L=-y^{(i,j)}log(g(w\cdot x+b))-(1-y^{(i,j)})log(1-g(w\cdot x+b))$

那么整体的成本函数就表示为：

$J=\sum_{r(i,j)=1}^{}L(f(w,b,x),y^{(i,j)})$

均值归一化：

假设我们此时引入一个新用户，该用户没有对任何一部电影进行过评分。如果按照之前的模型，由于在成本函数中引入了正则化项，且该用户没有评分，即成本函数第一项没有用任何影响，那么此时得出的 $w\approx 0$ ，而 $b\approx$ 初始化值。可见如果采用这样得出的参数进行预测，结果是非常不准确的，因此我们需要对原始数据进行均值归一化。

我们对原始数据矩阵的每一行求平均值，即计算每一部电影的平均得分，得到均值向量 $\mu$ ，之后对原始数据更新为原始数据 $-\mu$ 。这样得到的预测结果应该是：

$y^{(i,j)}=w\cdot x+b+\mu$

此时同样由于存在正则化项，得出的 $w\approx 0$ ，而 $b\approx$ 初始化值，若初始值取0，则预测的新用户对于每一部电影的评分都将是原来这部电影的平均得分。相较于原始数据得出的结果，显然这次结果更为合理。并且，进行均值归一化还能略微的提高运行速度。

除了对行求平均外，我们也可以对列进行平均，即计算每一个用户对于看过的电影的平均评分情况，这种情况更适合出现一部新电影时，预测不同用户对其的评分结果。

如何进行推荐：

假设目前已经完成了前面的建模，那么对于某一个用户，应该对其推荐什么样的项目？结合协同过滤算法的内容，我们可以通过该算法得到每一个项目的特征向量 $x^{(i)}$ ，虽然该向量通常是难以理解的，很难通过对用户喜欢项目得出的特征向量具体的理解信息来进行推荐。因此实际会推荐与特征向量 $x^{(i)}$ 相似的向量 $x^{(k)}$ 对应的项目k，相似定义如下：