模电基础:放大电路的频率响应(2)
目录
一、电流放大倍数β与频率的关系
二、放大倍数β的波特图
三、思考为什么混合π要使用跨导gm
(1)跨导gm:剥离频率影响的 “核心控制参数”
(2)混合π模型:拆分 “控制本质” 与 “频率影响”
(3)发射结小信号电阻rb'e:辅助理解的 “静态关联参数”
四、单极共射放大电路的频率响应
(1)中频段电压放大倍数
(2)低频段放大倍数
(3)高频放大倍数
(4)全频段放大倍数
五、带宽增益积
六、多级共射放大电路的频率响应
(1)中频段增益效果
(2)下降斜率编辑
(3)截止频率
在上一篇文章中,我们初步了解了高通、低通电路在不同频率输入信号时,对输出信号的衰减程度差异。明白了电流放大倍数β其实是受到频率的影响的,比如在低通电路中,当频率较高时,输出信号衰减程度大,所以放大倍数β减小。所以我们才需要用跨导gm这样一个与频率无关的元素、以及Ube的关系来表示输出回路电流iC的大小。
我们仅仅是定性的分析了“频率与β有关”,但是他们之间具体是一个什么函数的关系,我们并未了解,于是这篇文章由此开始。
一、电流放大倍数β与频率的关系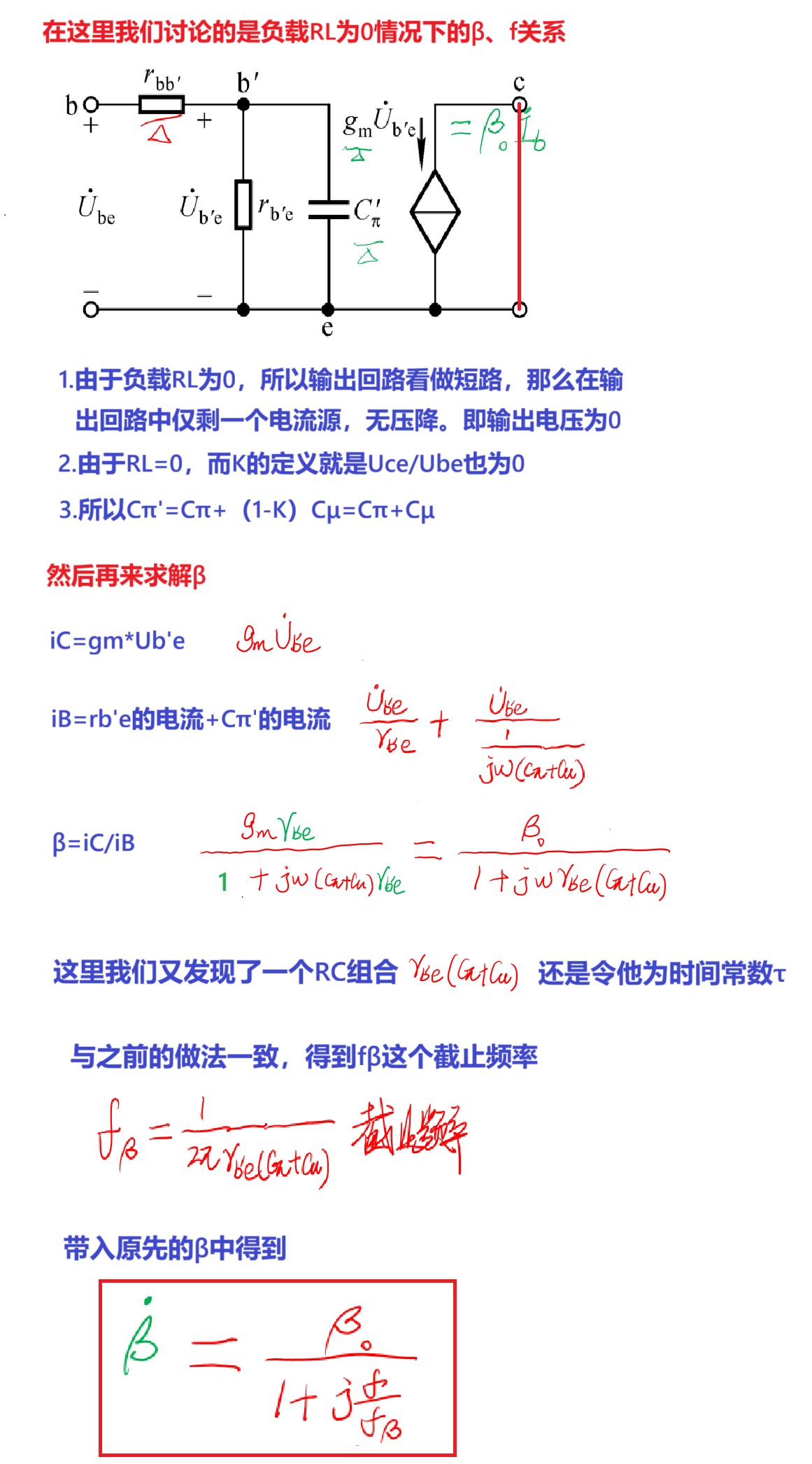
注意:
1.这里面的角速度w是输入信号的角速度,不过不重要,因为在β中被转化成了f,我们应当更加关心f而不是w。
2.然后这个fβ是针对于该混合π模型计算出的上限截止频率,因为混合π模型是低通电路。相当于对我们上一节的低通电路的实际运用。
二、放大倍数β的波特图
再画出曲线图: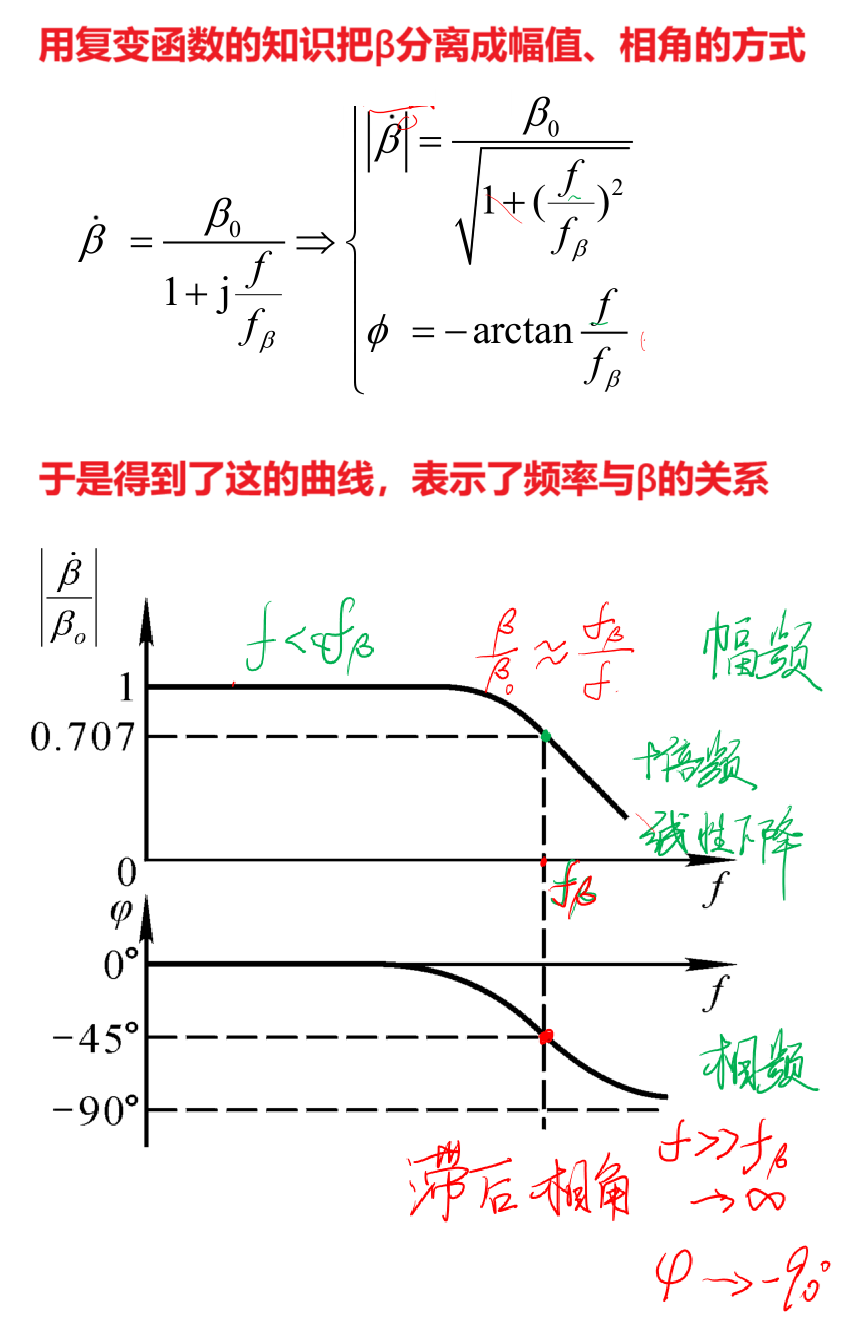
注意这里的β0是中频带(通频带)的电流放大倍数,因为在通频带时,无论是高通电路还是低通电路,他们对于输入信号都几乎没有衰减,所以认为电流放大倍数β稳定不变,也就是β0在中频带稳定。
简单来说:输入信号的频率 f 超过fβ 后,晶体管的电流放大倍数 β会因 “内部低通电路的衰减” 而明显下降。
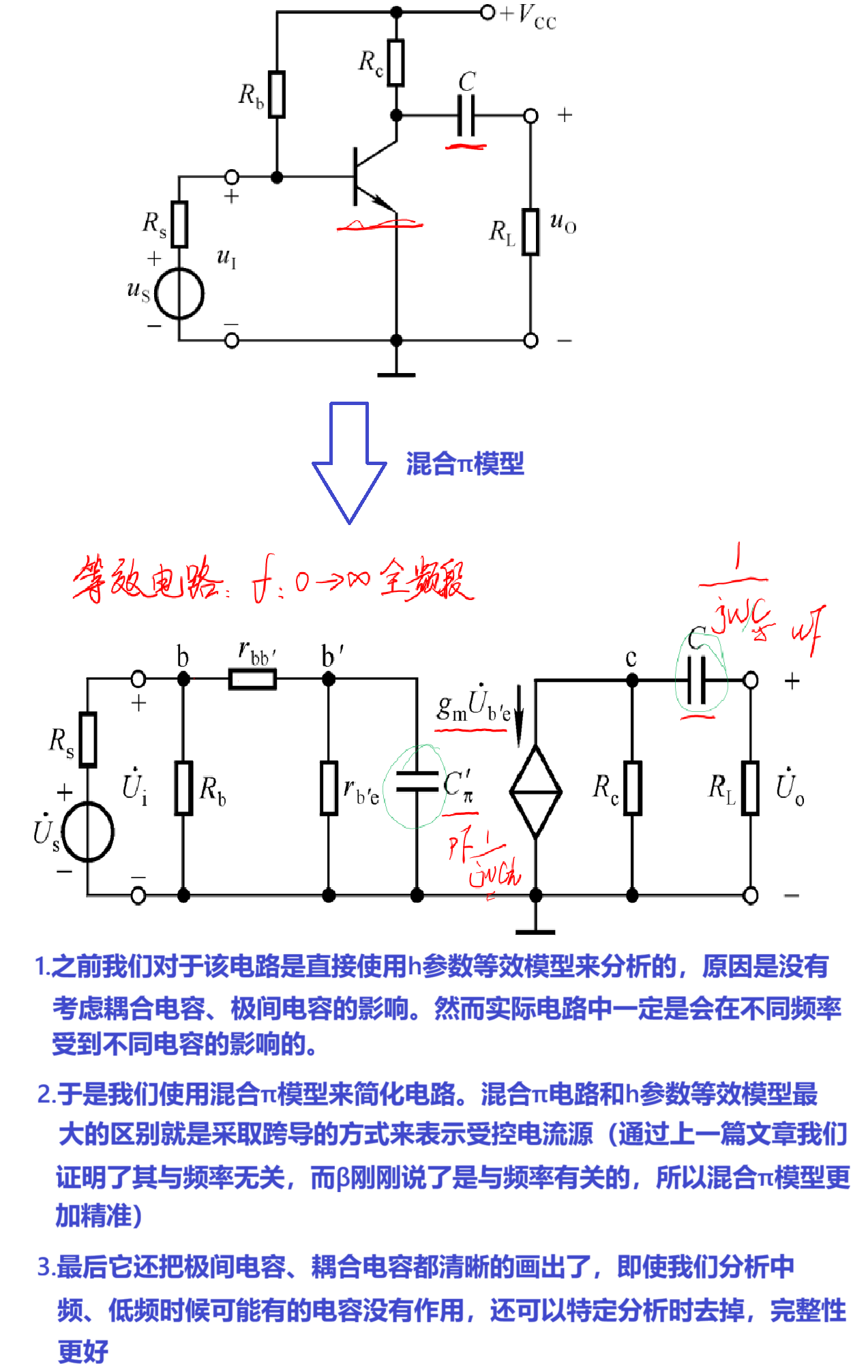
三、思考为什么混合π要使用跨导gm
我们上一篇文章清除的说到跨导gm是利用中频段的放大倍数β0推导出来的,那么我产生了一个问题,中频段推导出来的东西为什么能在全频段通用呢?
(1)跨导gm:剥离频率影响的 “核心控制参数”
跨导本质定义的就是Ub'e对ic的控制能力,只不过这里我们为了方便运算,采取中频段的参数来计算,刚好能约掉rb'e中的β。而rb'e本身也和频率无关,只是可以用β0来测量。
(2)混合π模型:拆分 “控制本质” 与 “频率影响”
延用β会有ib电流、β两个变化量,使用跨导仅仅有Ub'e一个变化量。
(3)发射结小信号电阻rb'e:辅助理解的 “静态关联参数”
四、单极共射放大电路的频率响应
我们已经学习了高频等效模型、h参数等效模型、以及高通、低通电路对电路的影响。那么我们这里使用他们来分析一下共射放大电路的频率与输出电压问题。
(1)中频段电压放大倍数
在中频段的时候,其实回归到了我们最开始利用h参数求解的过程,此时我们认为耦合电容较大可以忽略,且频率不够让极间电容产生明显影响,视为开路。可以这样理解:左边部分是低通电路、右边部分是高通电路,中频段既属于低通的通频带也属于高通的通频带,所以两个电容都不影响信号的正常传递,即都视作无影响。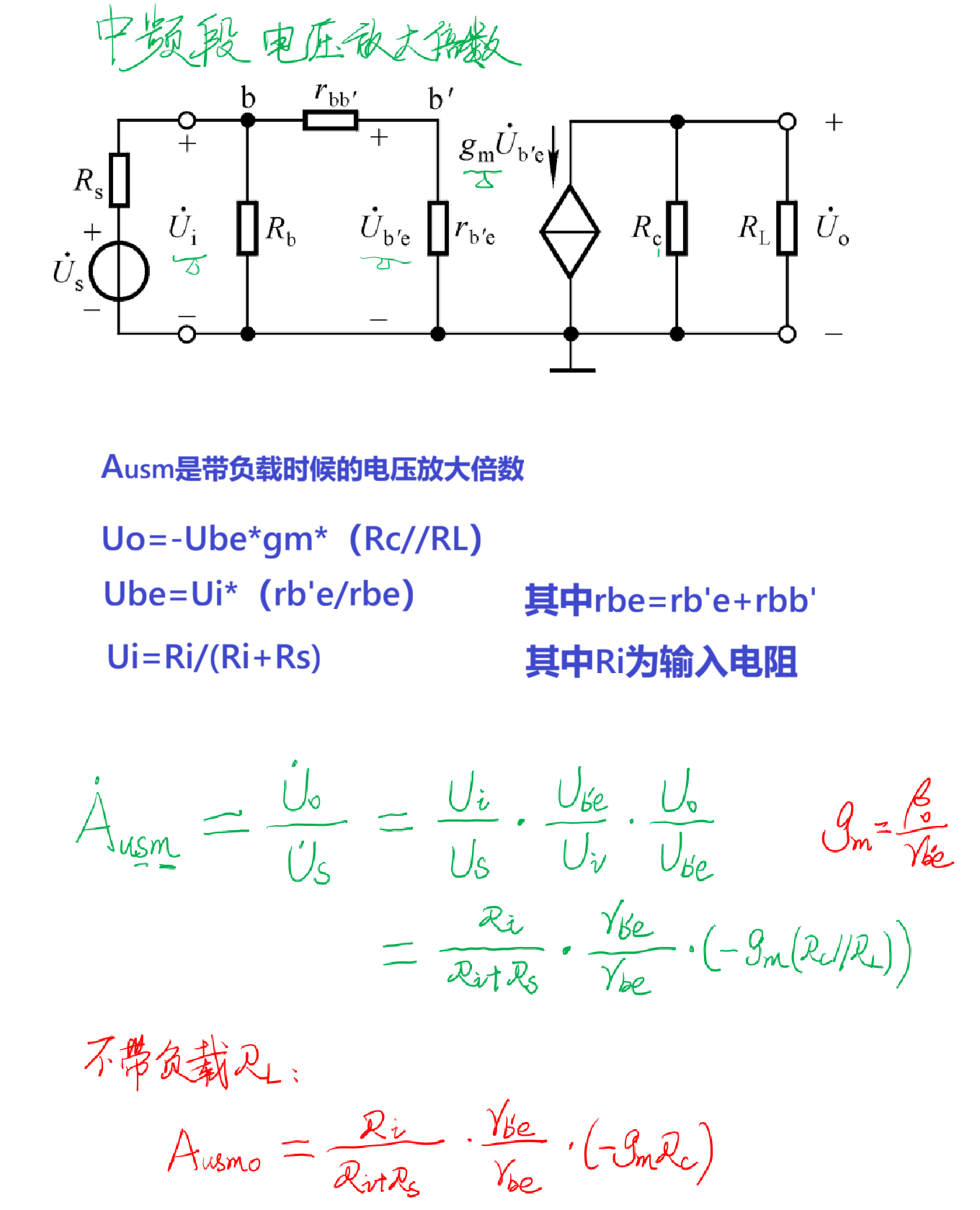
(2)低频段放大倍数
和上面类似的分析方法,低频信号可以正常通过左边的低通电路,而不能正常通过高通电路,所以极间电容可以忽而耦合电容必须画出来。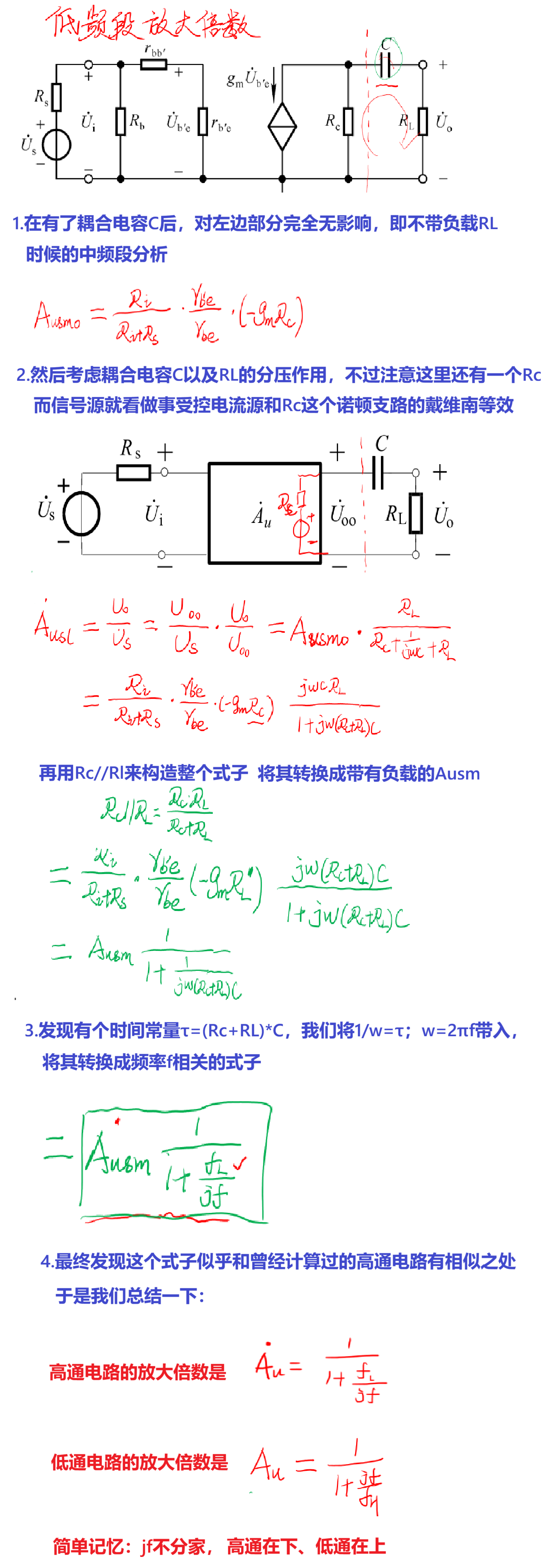
以后我们在求解放大倍数的时候,可以直接套用这个公式。然后Ui就是中频段的放大倍数Ausm。
现在问题变成了求解fL或者fH这个下限/上限截止频率。
我们只需要在对应的高通或者低通电路中找到总的R和电容C即可得到时间常数τ,而τ与f又有一个对应关系。
比如在求低频放大倍数的时候,RC回路就是电容C、Rc、负载RL,所以τ=(Rc+RL)*C,f=1/2πτ。
还有一点需要强调的就是这个时间常数RC是在电容所在回路求得的,但是这个回路的范围需要清晰,在求整个电路的放大倍数时候τ就是要把所有的电阻都包含进去。而仅仅计算三极管本身特性,比如放大倍数β时,则仅仅是电容所在的最小回路。
(3)高频放大倍数
有了上面经验,在这里,极间电容必须体现出来,高通电路可以忽略。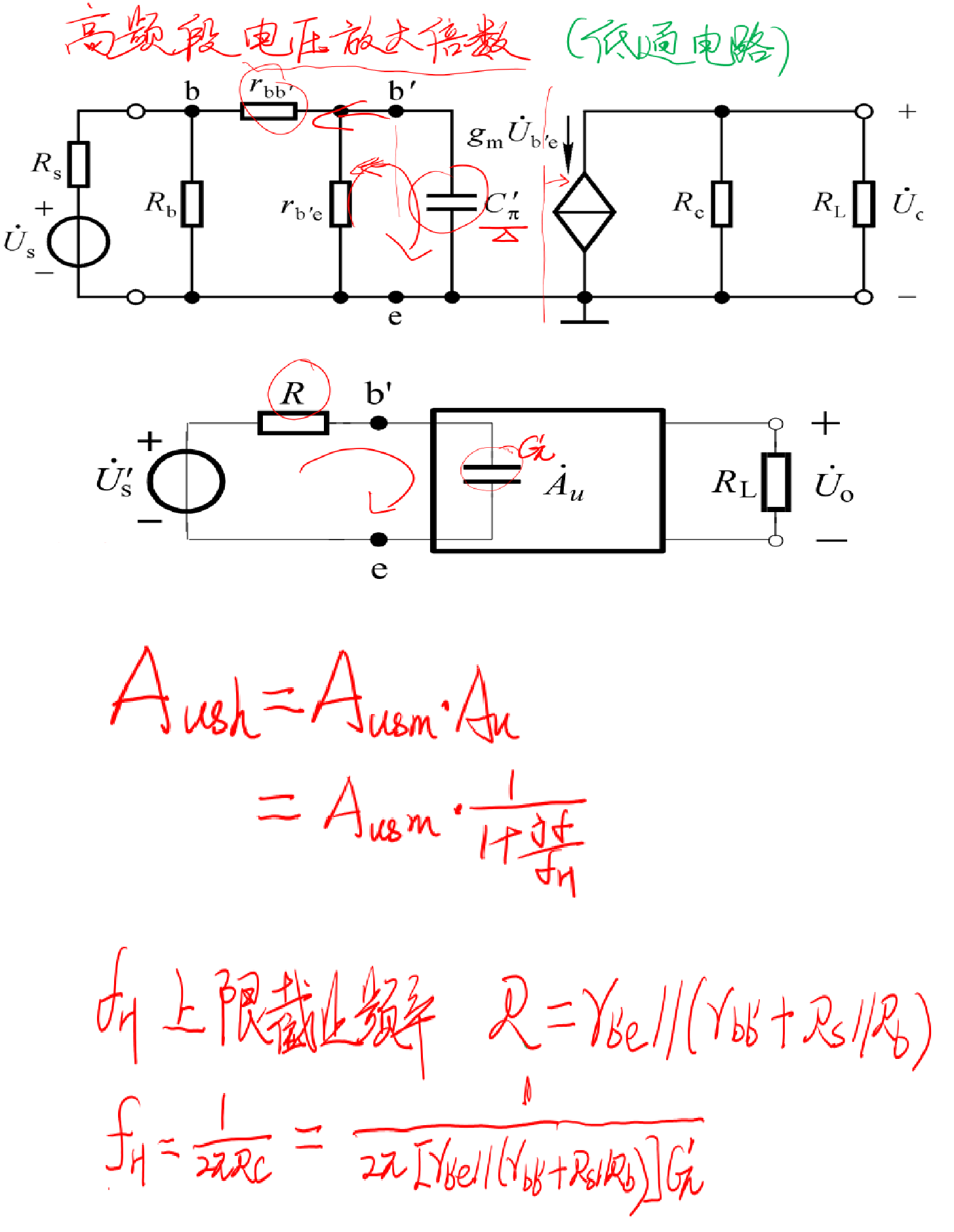
(4)全频段放大倍数
将上述的融合到一起,就得到了全频段。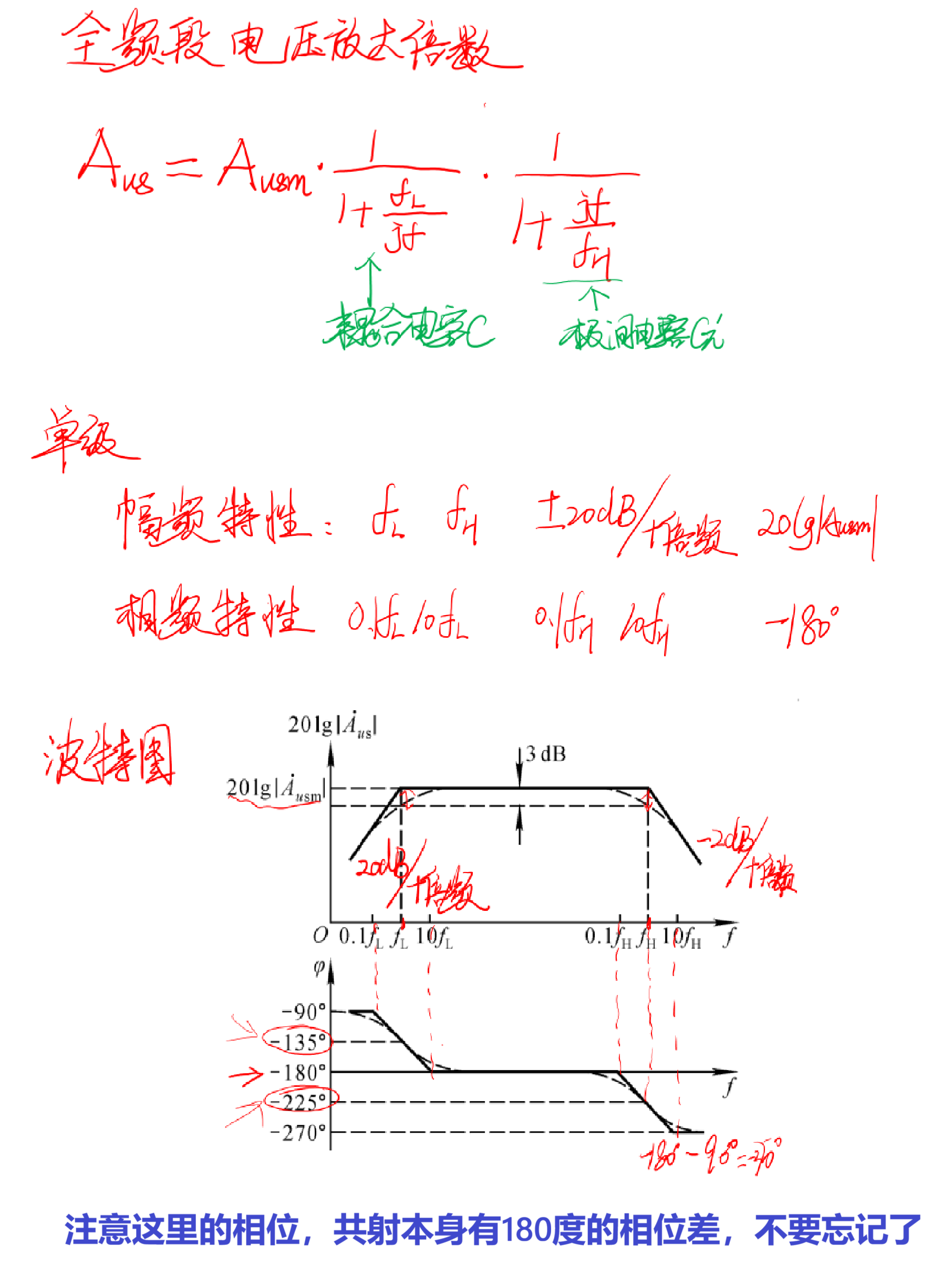
五、带宽增益积
带宽增益积指的是同频带*总的放大倍数,经过计算发现他们在每一款电路中都是一个常数,下面的推导过程不需要记忆,只需要明白一点:当你想要提高增益的时候,带宽一定会减小;反之想要提升带宽,则增益一定会减小。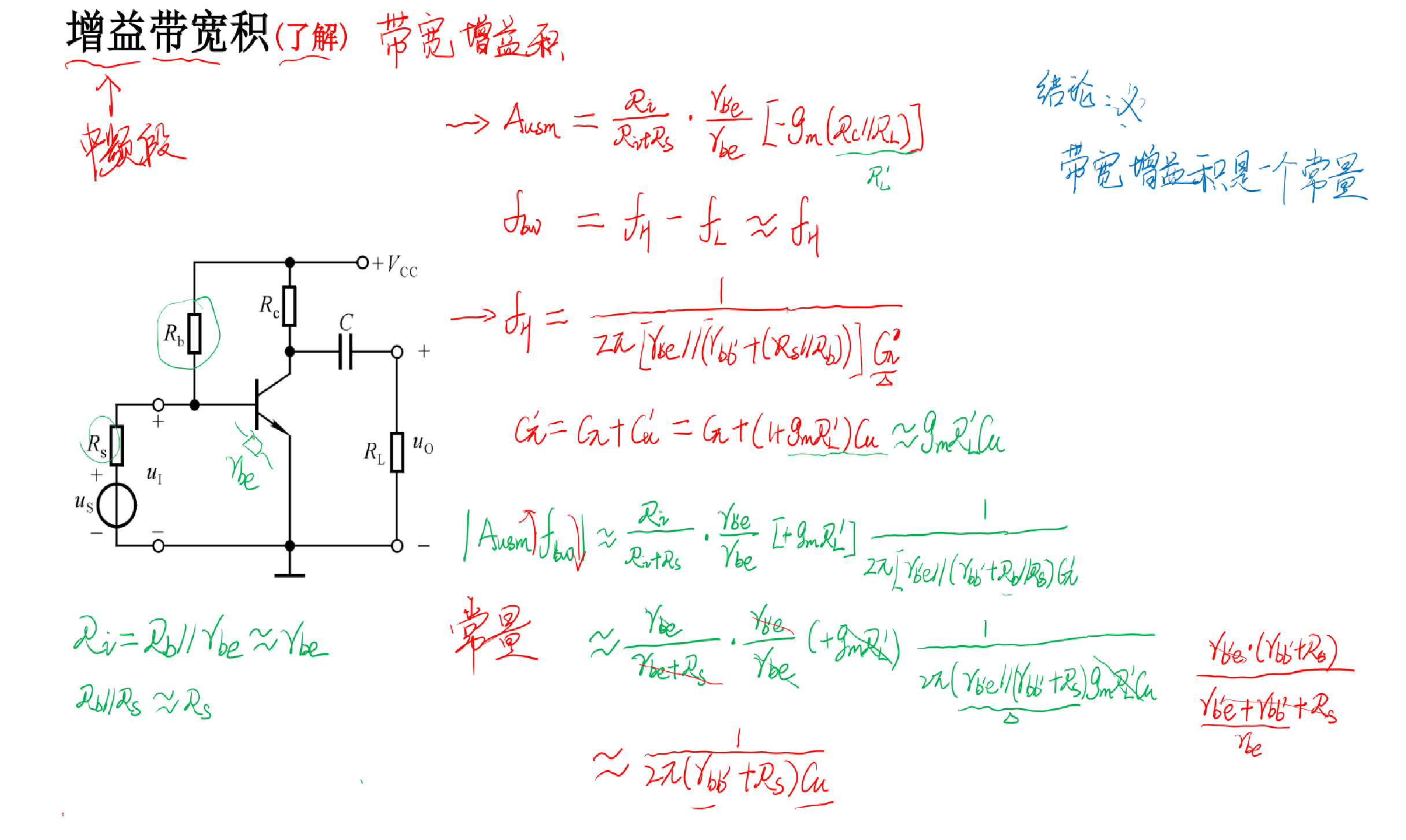
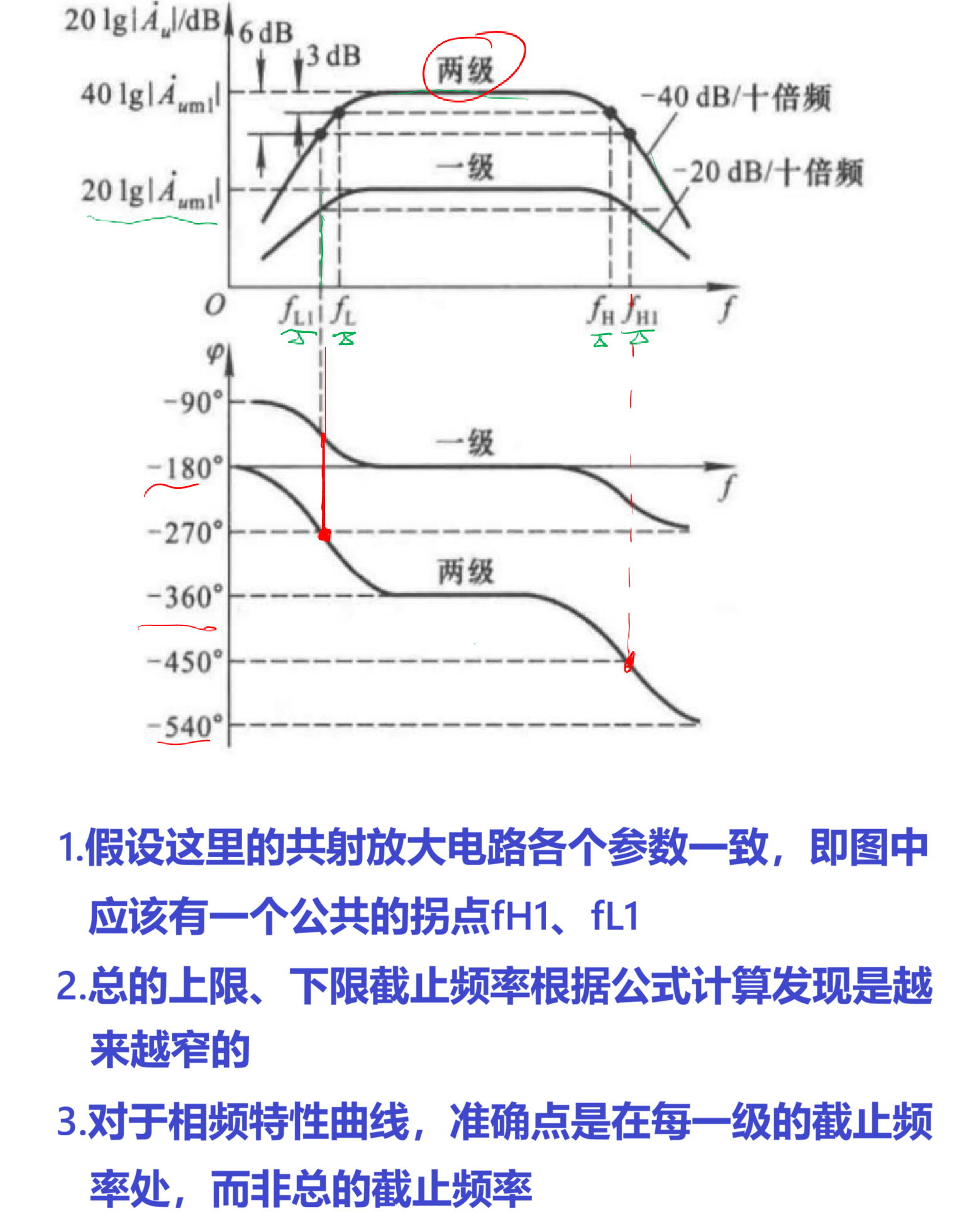
六、多级共射放大电路的频率响应
我们知道一个集成运放往往是用多级电路组合而成的,而频率响应这一章节也不例外,我们分析的是耦合电容、极间电容对频率的响应作用。
(1)中频段增益效果
(2)下降斜率
(3)截止频率
对于波特图中的拐点是每一级单独的,也就是说有多少级理论上就有多少个拐点,但是如果每一级都是一模一样的,则拐点会重合。
然后总的fL和fH呈现下面的形式,有一个类似倒数的关系。其中根号下是每一级的上限/下限截止频率的求和。对于这里我们并不需要知道怎么来的,简单记忆即可。但是可能出现上限和下限的斜率不同,此时就说明是有多少个耦合电容/极间电容的影响了。比如下限斜率为20,说明只有一个高通电路,那么在计算总的fL的时候,直接就是原fL。这是这里求和需要注意的点:有多少个高通或者低通电路,才对应累加多少个。