结构化特征生成推进广度学习:2025年深度学习领域的重要突破
📖 原文论文:Advancing Broad Learning Through Structured
FeatureGeneration
🔗 论文地址:https://doi.org/10.1016/j.eswa.2025.129948
✍️ 作者:MarioMallea,ÀngelaNebot,FranciscoMugica
🎉 发布时间:2025年10月
🎯 关键词:广度学习系统、随机神经网络、特征生成、结构化学习、高效计算
一、研究背景与意义
深度神经网络(DNNs)在大数据场景下表现出色,但在数据稀缺场景中面临严重挑战,包括过拟合、高计算成本和训练时间长等问题。这使得DNNs在数据收集昂贵或不可行的实际应用中受到限制。
广度学习系统(BLS) 作为一种高效的替代方案应运而生。与深度网络不同,BLS构建宽而浅的网络结构,通过随机特征映射和线性优化实现高效学习。然而,传统BLS依赖于独立同分布(i.i.d.)的随机特征生成,这种方法虽然计算高效,但容易产生冗余和次优的特征表示。
论文提出的结构化广度学习系统(SBLS) 通过引入结构化基函数,重新定义了特征生成方式,在保持BLS高效性的同时,显著提升了性能、鲁棒性和可解释性。
二、论文整体结构与主要贡献
论文采用严谨的学术结构:理论基础 → 方法设计 → 理论分析 → 实验验证 → 应用展望。

图1:论文组织结构图
主要贡献可总结为四点:
方法创新:首次提出结构化广度学习系统,用设计的基函数替代随机特征生成
理论保证:证明SBLS具有通用逼近性质,为方法有效性提供理论基础
全面验证:在多个分类和回归任务上系统验证SBLS的优越性
实用价值:保持BLS的高效性和增量学习能力,适合实际部署
三、结构化广度学习系统核心方法
1. 系统架构设计
SBLS重新定义了BLS的核心组件,将随机线性映射替换为设计的基函数。系统包含两个主要部分:
特征节点:使用结构化基函数生成特征表示
增强节点:通过随机组合基函数并应用非线性激活来捕获复杂关系
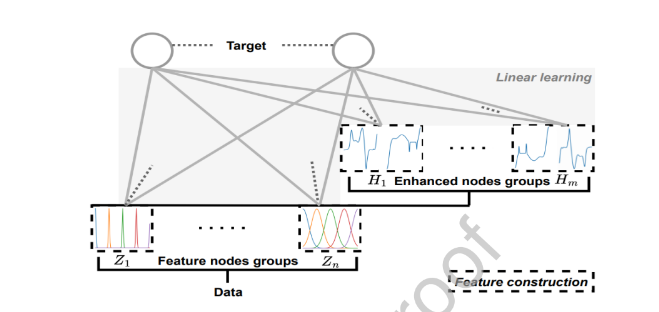
图2:结构化广义学习系统(SBLS)框架示意图。该模型包含多个特征节点组Z 1 、···、Z n,这些节点通过输入数据的结构化转换生成,以及增强节点H 1 、···、H m,用于进一步丰富表征信息。所有特征组均与目标层线性连接,这种设计既保证了高效训练能力,又支持具有表达力的结构化特征构建
2. 三种基函数设计
论文提出了三种基函数,每种都有明确的数学定义和参数控制:
高斯基函数
ϕ_i^L[j] = \frac{1}{\sqrt{2πσ_L^2}} e{-\frac{(j-c_i)2}{2σ_L^2}}
特点:局部平滑模式,适合捕获局部特征依赖
参数:中心点c_i控制关注位置,方差σ_L²控制感受野大小
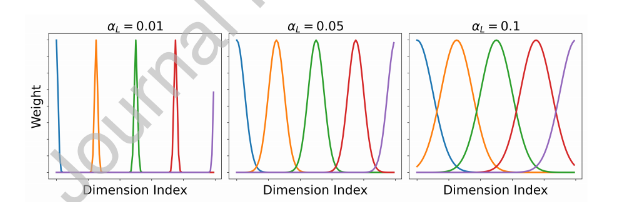
图3:通过高斯基生成结构化特征
Sigmoid基函数
σ_i^L[j] = \frac{1}{1 + e^{-α_L(j-c_i)}}。
特点:累积激活模式,适合捕获累积效应特征
参数:c_i控制中心点,α_L控制斜率
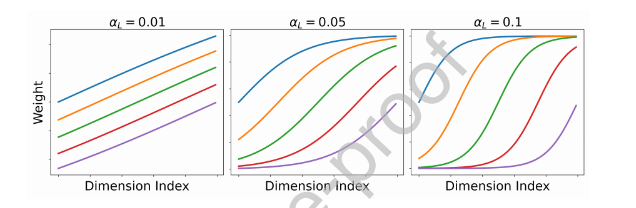
图4:通过Sigmoid基生成结构化特征
GELU基函数
基于高斯误差线性单元,结合了ReLU和Dropout的思想:
Gelu_i^L[j] = 0.5α_L(x-c_i){1 + \tanh(\sqrt{\frac{2}{π}}ξ)}
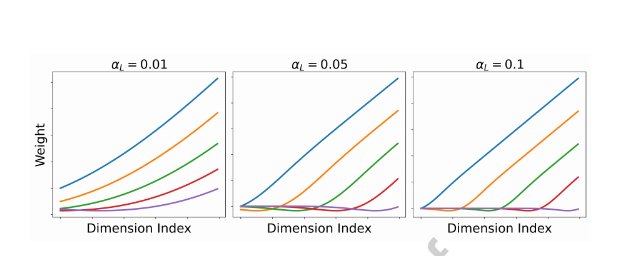
图5:通过Gelu基生成结构化特征。

图6:特征节点之间生成的相关性。
---四、理论分析与保证
论文从理论上证明了SBLS的通用逼近能力,这是该方法有效性的重要理论基础
定理1
对于任意连续函数f∈C ([0,1] d )及任意紧集K∈[0,1]d(其中d为整数),存在由SBLS构造µ诱导的概率测度所定义的SBLS网络序列{ ˆ f n,m },使得
limₙ,ₘ→∞ ρ_K(f, 𝑓̂ₙ,ₘ; μ) = 0
这一普适近似特性源自大数定律(BLS)。而SBLS的近似结果则通过蒙特卡洛估计的重新参数化获得,类似于方差缩减方法。实际上,SBLS定义了一种权重生成方案,能够产生空间填充概率分布。举例来说,神经元每个随机权重w i j的表达式为b ij + ϵ~ N(b ij, 1),其中b ij表示实值基函数。因此广义而言,大数定律保证了我们生成的随机特征集合能够模拟未知特征集合。当考虑无限数量节点时,蒙特卡洛近似(公式A.2)将收敛于目标函数(公式A.1)的积分形式。
对方差降低、泛化复杂度和收敛速率的进一步研究是未来研究的方向。
五、实验验证与性能评估
1. 数据集与实验设置
论文在多个标准数据集上进行了全面评估:
分类任务:
MNIST:手写数字识别(60,000训练,10,000测试)
Coil100:3D物体识别(5,000训练,2,000测试)
Isolet:语音字母识别(1,092训练,468测试)
回归任务:
Abalone:年龄预测
Weather Izmir:温度预测
Boston Housing:房价预测
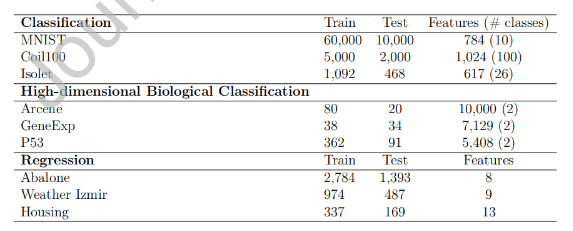
图7:数据集统计
2. 性能结果
关键发现:
SBLS在所有数据集上显著优于传统BLS
高斯基函数在图像分类任务中表现最佳
Sigmoid和Gelu在回归任务中更有优势

图 8:三种SBLS变体和经典BLS在分类和回归任务上的性能结果。
3. 计算效率
SBLS保持了BLS的高效特性,在标准CPU上完成10次MNIST训练仅需4.0分钟,比随机森林(14.0分钟)和多层感知机(14.7分钟)快3.5倍以上,比需要GPU的TabM方法快6倍
六、性能评估指标
1. 抗噪声鲁棒性
在加入1%-30%高斯白噪声的测试中,SBLS表现出更强的鲁棒性。传统BLS在噪声环境下性能下降明显,而SBLS各变体保持了稳定的性能表现 。
2. 可解释性提升
通过可视化最重要的特征,研究发现SBLS学习的特征更加连贯和有意义:
传统BLS:重要特征通常是分散、孤立的像素
SBLS:重要特征形成平滑路径,往往与数字形状一致
这种可解释性的提升使得模型决策过程更加透明。
3. 高维数据处理能力
在生物信息学等高维数据集(如Arcene、GeneExp、P53)上的实验表明,SBLS能够有效处理维度压缩,在保持90%维度压缩率时仍能维持竞争性性能。
4. 领域知识集成
论文展示了如何将领域知识直接集成到基函数设计中。在MNIST数据集上,通过设计考虑图像空间结构的基函数,性能从97.39%进一步提升到97.75%
七、应用、挑战与未来趋势
应用场景
SBLS的实用价值体现在多个方面:
- 边缘计算低计算需求适合资源受限环境
- 实时系统:快速训练适合动态更新场景
- 数据稀缺领域:在医疗、金融等数据收集困难的领域有特殊价值
- 可解释性要求高的场景:如医疗诊断、金融风控
技术优势
- 即插即用:无需复杂调参,易于部署
- 增量学习:支持在线更新,适应动态环境
- 硬件友好:在标准CPU上即可高效运行
八、局限性与未来方向
当前局限
基函数组合与数据拓扑的关系需要进一步研究
在复杂结构化输入(如图形、序列)上的性能有待验证
需要更多真实场景的部署验证
未来研究方向
基函数扩展:探索更多类型的基函数和组合准则
理论深化:研究方差减少、泛化复杂度和收敛速率
应用拓展:时间序列预测、推荐系统、半监督学习等
跨领域迁移:将结构化特征生成思想应用到其他随机神经网络
九、总结
《Advancing Broad Learning Through Structured Feature Generation》在2025年提出了一个简单而有效的想法:用结构化基函数替代随机特征生成,这一改变带来了显著的性能提升。
核心启示:
性能与效率可兼得:SBLS在提升性能的同时保持了BLS的高效特性
结构化带来可解释性:设计的基函数使得学习过程更加透明
实用导向的设计:从实际应用需求出发,解决了数据稀缺、计算资源有限等现实问题
理论实践结合:既有理论保证,又有充分实验验证
这项工作为随机神经网络和高效学习系统提供了新的思路,特别是在边缘计算、实时系统和资源受限环境中具有重要的应用前景。SBLS的成功表明,在追求更深更复杂的网络结构之外,智能的特征生成同样可以带来显著的性能提升。
