多视图几何--密集匹配--视差平面推导

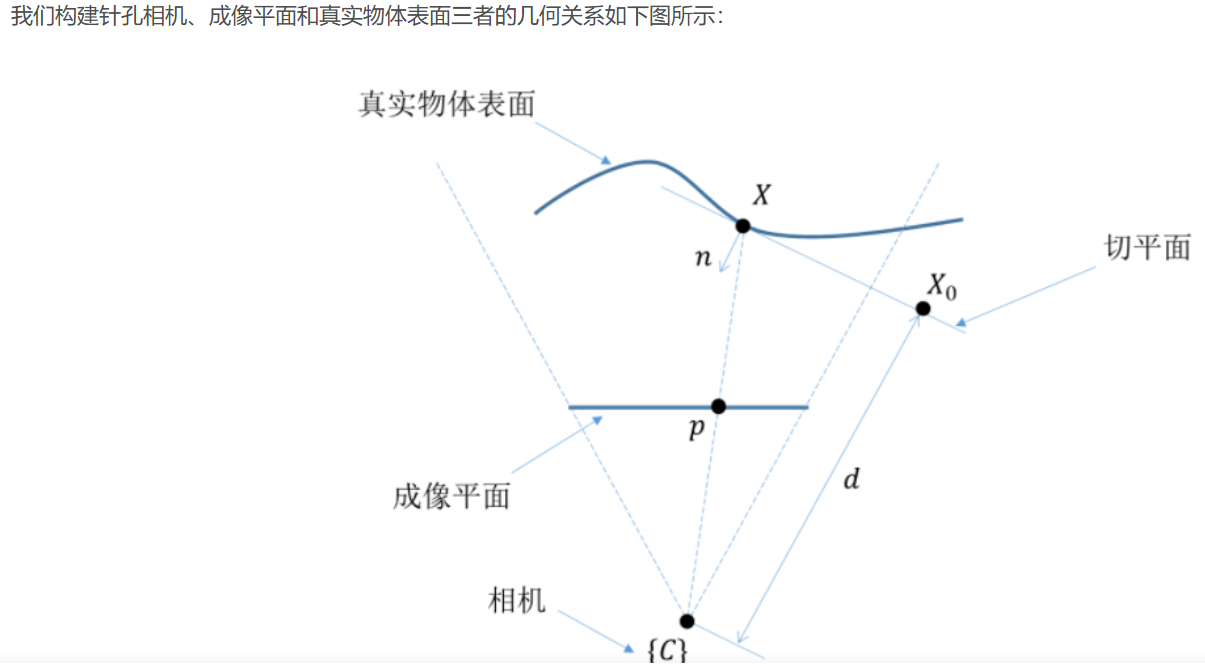
方法1

视差平面推导

首先，切平面的数学表达式为：$n^{T}X+d=0$
推理过程如下：
$$\begin{array}{rl}& n^T\left(X-X_0\right)=0,X_0=-d\cdot n\\ & \Downarrow \\ & n^{T}X-n^T{X}_0=0\\ & \Downarrow \\ & n^{T}X+n^{T}n\cdot d=0\\ & \Downarrow \\ & n^{T}X+d=0\end{array}$$

• $X$ 是位于真实物体表面上的空间点（相机坐标系下）
• $n$ 是切平面的法向量
• $X_0$ 是位于切平面上的空间点（相机坐标系下）
• $p$ 是 $X$ 在成像平面的投影点（图像像素坐标系下）
• $d$ 表示相机原点到切平面的法线距离

其次，空间点 $X$ 和成像平面投影点 $p$ 之间存在如下关系：

$$\begin{array}{c}p=(1/z)\cdot K\cdot X\\ X=z\cdot K^{-1}\cdot p\end{array}$$
其中，$z$ 是空间点 $X$ 的 $z$ 轴坐标，即投影点 $p$ 的深度

因此，我们可以推导出，由切平面和投影点 $p$ 表示的深度 $z$ ：

$$\{\begin{array}{l}X=z\cdot K^{-1}\cdot p\\ n^{T}X+d=0\end{array}\Rightarrow z=-\frac{d}{n^T{K}^{-1}p}$$

由根据，双目几何结构中，视差和深度的对应关系：

$$z=\frac{B\cdot f_x}{d_p}$$

这里，$B$ 表示双目基线长度，$f_x$ 表示内参中的焦距，$d_p$ 表示视差。

因此，我们可以得到，由投影点 $p$ 表示的视差 $d_p$ ：

$$d_p=-\frac{B{f}_x}{d}{n}^T{K}^{-1}p=a_{f_p}{p}_x+b_{f_p}{p}_y+c_{f_p},p={\left[p_x,p_y,1\right]}^T$$

其中，$-\frac{B{f}_x}{d}{n}^T{K}^{-1}$ 可以由 $a_{f_y},b_{f_p},c_{f_p}$ 这三个参数表示。

进一步展开$-\frac{B{f}_x}{d}{n}^T{K}^{-1}$ ：

步骤1: 计算内参矩阵的逆$K^{-1}$

假设内参矩阵$K$为：

$$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

则其逆矩阵$K^{-1}$为：

$$K^{-1}=\left[\begin{array}{ccc}\frac{1}{f_x}& 0& -\frac{c_x}{f_x}\\ 0& \frac{1}{f_y}& -\frac{c_y}{f_y}\\ 0& 0& 1\end{array}\right]$$

步骤2: 计算$K^{-1}p$

给定$p=[p_x,p_y,1{]}^T$，计算：

$$K^{-1}p=\left[\begin{array}{ccc}\frac{1}{f_x}& 0& -\frac{c_x}{f_x}\\ 0& \frac{1}{f_y}& -\frac{c_y}{f_y}\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{p}_x\\ p_y\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{p_x-c_x}{f_x}\\ \frac{p_y-c_y}{f_y}\\ 1\end{array}\right]$$

步骤3: 计算$n^T{K}^{-1}p$

给定$n=[n_x,n_y,n_z{]}^T$，计算：

$$n^T{K}^{-1}p=[n_x,n_y,n_z]\left[\begin{array}{c}\frac{p_x-c_x}{f_x}\\ \frac{p_y-c_y}{f_y}\\ 1\end{array}\right]=n_x\frac{p_x-c_x}{f_x}+n_y\frac{p_y-c_y}{f_y}+n_z$$

步骤4: 代入视差公式

将$n^T{K}^{-1}p$代入视差公式：

$$d_p=-\frac{B{f}_x}{d}\left(n_x\frac{p_x-c_x}{f_x}+n_y\frac{p_y-c_y}{f_y}+n_z\right)$$

步骤5: 展开并简化表达式

展开括号：

$$d_p=-\frac{B{f}_x}{d}\cdot n_x\frac{p_x-c_x}{f_x}-\frac{B{f}_x}{d}\cdot n_y\frac{p_y-c_y}{f_y}-\frac{B{f}_x}{d}\cdot n_z$$

简化每一项：

$$d_p=-\frac{B{n}_x}{d}(p_x-c_x)-\frac{B{f}_x{n}_y}{d{f}_y}(p_y-c_y)-\frac{B{f}_x{n}_z}{d}$$

步骤6: 进一步展开为$p_x$和$p_y$的线性形式

展开括号中的项：

$$d_p=-\frac{B{n}_x}{d}{p}_x+\frac{B{n}_x{c}_x}{d}-\frac{B{f}_x{n}_y}{d{f}_y}{p}_y+\frac{B{f}_x{n}_y{c}_y}{d{f}_y}-\frac{B{f}_x{n}_z}{d}$$

合并常数项：

$$d_p=\left(-\frac{B{n}_x}{d}\right)p_x+\left(-\frac{B{f}_x{n}_y}{d{f}_y}\right)p_y+\left(\frac{B{n}_x{c}_x}{d}+\frac{B{f}_x{n}_y{c}_y}{d{f}_y}-\frac{B{f}_x{n}_z}{d}\right)$$

步骤7: 定义系数$a_{f_p},b_{f_p},c_{f_p}$

根据上式，令：

$$a_{f_p}=-\frac{B{n}_x}{d}$$

$$b_{f_p}=-\frac{B{f}_x{n}_y}{d{f}_y}$$

$$c_{f_p}=\frac{B{n}_x{c}_x}{d}+\frac{B{f}_x{n}_y{c}_y}{d{f}_y}-\frac{B{f}_x{n}_z}{d}$$

最终视差平面公式

因此，视差平面公式可写为：

$$d_p=a_{f_p}{p}_x+b_{f_p}{p}_y+c_{f_p}$$

其中系数$a_{f_p},b_{f_p},c_{f_p}$由上述表达式定义。

方法2

1. 问题设定

投影模型：使用针孔相机模型，内参矩阵 $K$ 为：
$$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

其中 $f_x,f_y$ 是焦距（像素单位），$(c_x,c_y)$$是主点。

左右相机：假设已进行立体校正，两相机光轴平行、x 轴对齐，只在 x 方向有平移 $b$（基线长度，单位为米）。
左相机坐标系 = 世界坐标系（方便起见）。
右相机相对于左相机位姿为：$(R=I,T=[-b,0,0{]}^T)$。

三维空间平面（在左相机坐标系下）：
点法式表示：

$$\mathbf{n}\cdot \mathbf{P}=d_0$$

其中 $\mathbf{n}=[n_x,n_y,n_z{]}^T$ 是平面法向量（单位向量），$\mathbf{P}=[X,Y,Z{]}^T$ 是三维点，$d_0$ 是原点到平面的有符号距离（米）。

---

2. 左相机投影

左相机内参矩阵 $K$，投影方程（齐次坐标）：

$${\mathbf{p}}_l=K\mathbf{P}$$

即：

$$\left[\begin{array}{c}{u}_l\\ v_l\\ 1\end{array}\right]\equiv \left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$

所以：

$$u_l=f_x\frac{X}{Z}+c_x,v_l=f_y\frac{Y}{Z}+c_y$$

或者反解：

$$X=Z\frac{u_l-c_x}{f_x},Y=Z\frac{v_l-c_y}{f_y}$$

---

3. 右相机投影

右相机坐标系中，同一个三维点 $$\mathbf{P}=[X,Y,Z{]}^T$$ 的坐标为：

$${\mathbf{P}}_r=R\mathbf{P}+T=\mathbf{P}+[-b,0,0{]}^T=[X-b,Y,Z{]}^T$$

右相机内参矩阵与左相机相同（已校正），所以：

$$u_r=f_x\frac{X-b}{Z}+c_x,v_r=f_y\frac{Y}{Z}+c_y$$

注意 $v_r=v_l$（已校正条件下）。

---

4. 视差定义

视差：

$$d=u_l-u_r$$

代入：

$$d=\left[f_x\frac{X}{Z}+c_x\right]-\left[f_x\frac{X-b}{Z}+c_x\right]=\frac{f_{x}b}{Z}$$

这是已知的视差-深度关系。

---

5. 将平面方程用图像坐标表示

平面方程：

$$n_{x}X+n_{y}Y+n_{z}Z=d_0$$

代入 $X=Z\frac{u_l-c_x}{f_x}$，$Y=Z\frac{v_l-c_y}{f_y}$：

$$n_{x}Z\frac{u_l-c_x}{f_x}+n_{y}Z\frac{v_l-c_y}{f_y}+n_{z}Z=d_0$$

两边除以 $Z$：

$$n_x\frac{u_l-c_x}{f_x}+n_y\frac{v_l-c_y}{f_y}+n_z=\frac{d_0}{Z}$$

---

6. 用视差 $d$ 替换 $Z$

由 $$d=\frac{f_{x}b}{Z}$$ 得：

$$\frac{1}{Z}=\frac{d}{f_{x}b}$$

代入平面方程：

$$n_x\frac{u_l-c_x}{f_x}+n_y\frac{v_l-c_y}{f_y}+n_z=\frac{d_0}{f_{x}b}d$$

---

7. 整理成 $d=a{u}_l+b{v}_l+c$ 的形式

记 $u=u_l$，$v=v_l$。

上式乘以 $f_x$：

$n_x(u-c_x)+n_y\frac{f_x}{f_y}(v-c_y)+n_z{f}_x=\frac{d_0}{b}d$

设 $$\alpha =\frac{f_x}{f_y}$$（像素纵横比倒数，如果$f_x=f_y$ 则 $\alpha =1$）。

于是：

$$n_{x}u+n_y\alpha (v-c_y)+n_x(-c_x)+n_z{f}_x=\frac{d_0}{b}d$$

即：

$$\frac{d_0}{b}d=n_{x}u+\alpha n_{y}v+[-n_x{c}_x-\alpha n_y{c}_y+n_z{f}_x]$$

因此：

$$d=\frac{b}{d_0}{n}_{x}u+\frac{b}{d_0}\alpha n_{y}v+\frac{b}{d_0}[-n_x{c}_x-\alpha n_y{c}_y+n_z{f}_x]$$

---

8. 最终视差平面公式

令：

$$a_p=\frac{b}{d_0}{n}_x$$

$$b_p=\frac{b}{d_0}\alpha n_y$$

$$c_p=\frac{b}{d_0}[-n_x{c}_x-\alpha n_y{c}_y+n_z{f}_x]$$

则：$d(u,v)=a_{p}u+b_{p}v+c_p$

其中 $d(u,v)$ 是像素坐标 $(u,v)$ 处的视差。

---

9. 说明

• 在立体匹配中，每个分割的超像素或窗口可以拟合一个视差平面 $d=a_{p}u+b_{p}v+c_p$。
• 这里的 $a_p,b_p,c_p$ 与三维空间平面参数 $(n_x,n_y,n_z,d_0)$ 及相机内参、基线有关。
• 如果平面是 fronto-parallel（$n_x=0,n_y=0,n_z=1$），则 $a_p=0,b_p=0$，$d(u,v)=\frac{b{f}_x}{d_0}$ 常数，即视差图是平的。

---

最终公式：

$$\boxed{d(u,v)=a_{p}u+b_{p}v+c_p}$$

其中系数与平面法向量、内参、基线的关系如上所示。

参数的几何意义

1. 参数 a和 b：
   • a：表示视差沿图像水平方向的变化率
   • b：表示视差沿图像垂直方向的变化率
   • 这两个参数直接反映了3D平面的法向量在图像域的投影
2. 参数 c：
   • 表示当 (px,py)=(0,0)时的视差值（考虑主点偏移后的参考视差）
3. 特殊情况：
   • 当 a=b=0a=b=0 时，视差平面退化为常数，对应于fronto-parallel平面（正对相机的平面）
   • 当 nx=ny=0 时，平面平行于图像平面，视差恒定

视差平面点法式与一般方程的转换

视差平面可以由法向量和平面上的某点表示：

$$n^T\left(X-X_0\right)=n^T\left[\begin{array}{l}x-x_0\\ y-y_0\\ z-z_0\end{array}\right]=0$$

其中，$n$ 表示视差平面的法向量，$X=[x,y,z{]}^T$ 是视差平面的任意点，$X_0={\left[x_0,y_0,z_0\right]}^T$ 是视差平面的某点。

点加法向量方程转换为通用参数方程：

$$a_f=-\frac{n_x}{n_z},b_f=-\frac{n_y}{n_z},c_f=\frac{n_x{x}_0+n_y{y}_0+n_z{z}_0}{n_z}$$

推导过程如下：

$$\begin{array}{rl}& n^T\left[\begin{array}{l}x-x_0\\ y-y_0\\ z-z_0\end{array}\right]=0\\ & \Downarrow \\ & n_x\left(x-x_0\right)+n_y\left(y-y_0\right)+n_z\left(z-z_0\right)=0\\ & \Downarrow \\ & z=-\frac{n_z}{n_z}x-\frac{n_y}{n_z}y+\frac{n_x{x}_0+n_y{y}_0+n_z{z}_0}{n_z}\end{array}$$

通用参数方程转换为点加法向量方程：

$$\begin{array}{c}{n}_x=\frac{a_f}{\sqrt{a_f^2+b_f^2+1}},n_y=\frac{b_f}{\sqrt{a_f^2+b_f^2+1}},n_z=\frac{-1}{\sqrt{a_f^2+b_f^2+1}}\\ z_0=a_f{x}_0+b_f{y}_0+c_f\end{array}$$

左右视差平面转换

这里需要补充说明，如何从将左视图的视差平面转换为右视图的视差平面：
首先，我们有左视图的视差平面：

$$d_l=a_p{x}_l+b_p{y}_l+c_p$$

由于，$x_r=x_l-d_l,y_r=y_l$ ，我们可得，

$$\begin{array}{c}{d}_l=a_p\left(x_r+d_l\right)+b_p{y}_r+c_p\\ \Downarrow \\ d_l=a_p{x}_r+a_p{d}_l+b_p{y}_r+c_p\\ \Downarrow \\ \left(1-a_p\right)d_l=a_p{x}_r+b_p{y}_r+c_p\\ \Downarrow \\ d_l=\frac{a_p}{1-a_p}{x}_r+\frac{b_p}{1-a_p}{y}_r+\frac{c_p}{1-a_p}\end{array}$$

由于，$d_r=-d_l$ ，即 $x_l=x_r-d_r$ ，左右视图匹配点的视差值是互为相反数，则：

$$d_r=\frac{a_p}{a_p-1}{x}_r+\frac{b_p}{a_p-1}{y}_r+\frac{c_p}{a_p-1}$$

从而，我们得到右视图的视差平面表达式。