当前位置： 首页 > news >正文

栈和队列：“单端吞吐”VS”双端通行“（第十讲）

news 2025/10/13 6:18:25

本文由本人精心创作，对你有帮助的小伙伴可以一键三连哦~

一. 栈

1.1 概念与结构

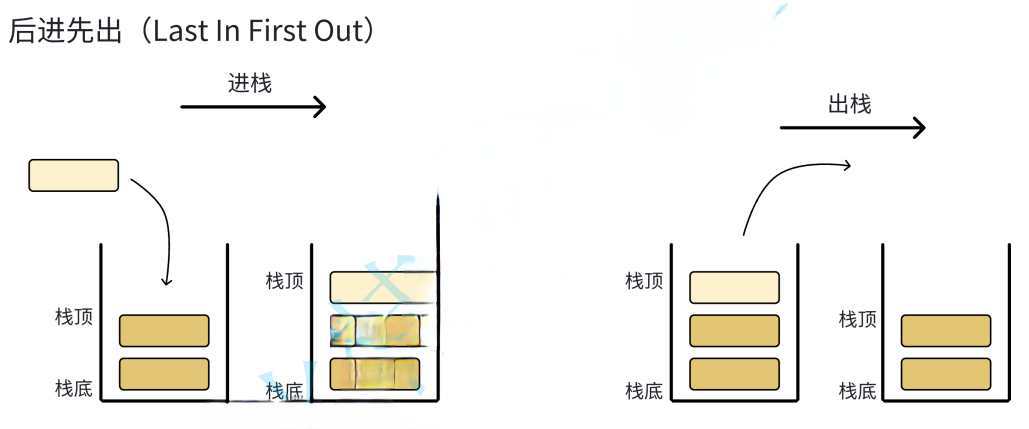
    栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。

    栈中的数据元素遵循后进先出的原则。栈可以看做一个水杯，只有上部可以接水倒水。

    压栈：栈的插入操作叫做进栈/入栈/压栈，入数据在栈顶。

    出栈：栈的删除操作叫做出栈，出数据也在栈顶。

1.2 栈的底层结构选型

   栈的实现一般可以使用数组或者链表实现，那到底选用这两种哪一个呢？那此时，我们就要从复杂度上来进行分析。

1.2.1数组评估（时间复杂度）

 若用数组来实现，我们可以让数组的尾部来作为栈顶，入栈和出栈的时间复杂度都是O（1）。

1.2.2链表评估（时间复杂度）

   若用链表来实现，我们可以让链表的头部来作为栈顶，入栈和出栈的时间复杂度也是O(1)。

   看来，使用数组和链表实现进栈出栈时间复杂度都是O（1），那到底选哪个？下面我们来评比二者的空间复杂度。

1.2.3（空间复杂度）

    如果要用数组来实现，比如说我要插入三个整型数据，那我只需申请三个int类型大小的空间。但是，如果用链表实现，我们得申请三个节点大小的空间，而三个节点的空间要比一个栈的空间大很多。

    用数组实现时申请空间无非就是四个字节四个字节的增加，而用链表实现申请空间申请的是一个节点一个节点，一个节点包括整型类型的数据（四个字节）+指针（四个字节），差不多八个字节，要比用数组插入数据所消耗的空间更大。

    综上：相对而言数组的实现结构更优一些，因为数组在尾上插入数据的代价（占用的内存空间）比较小。

二. 栈的实现

2.1 栈的初始化和销毁

//1.初始化
void STInit(ST* p)
{p->arr = NULL;p->size = p->capacity = 0;
}
//2.销毁
void STDestory(ST* p)
{if (p->arr)free(p->arr);p->arr = NULL;p->size = p->capacity = 0;
}

2.2 入栈

//3.入栈
ST* pushST(ST* p, STDataType x)
{//判断空间是否足够//1.当空间不够时if (p->top == p->capacity){int newcapacity == p->capacity ? 4 : 2 * p->capacity;STDataType* tmp = (STDataType*)realloc(p->arr, newcapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}p->arr = tmp;p->capacity = newcapacity;}//2.空间足够时p->arr[p->top++] = x;
}

2.3 出栈

//4.判断是否为空
bool STEmpty(ST* p)
{assert(p);return p->top == 0;
}
//5.出栈
void STPop(ST* p)
{if (!STEmpty(p))p->top--;
}

2.4 取栈顶元素和获取栈中有效元素个数

//6.取栈顶元素
STDataType STTop(ST* p)
{assert(!STEmpty(p));return p->arr[p->top - 1];
}
//7.获取栈中有效元素个数
int STSize(ST* p)
{assert(p);return p->top;
}

三. 队列

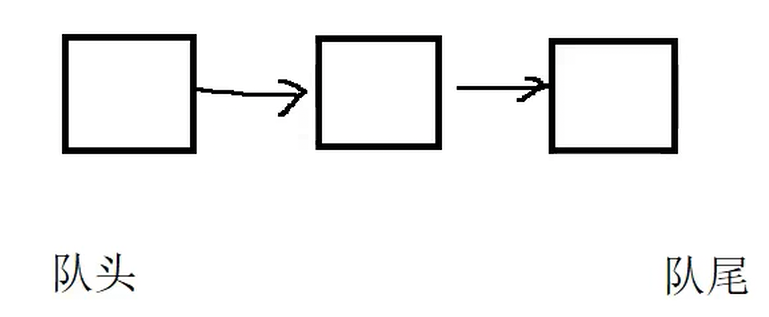
3.1 概念与结构

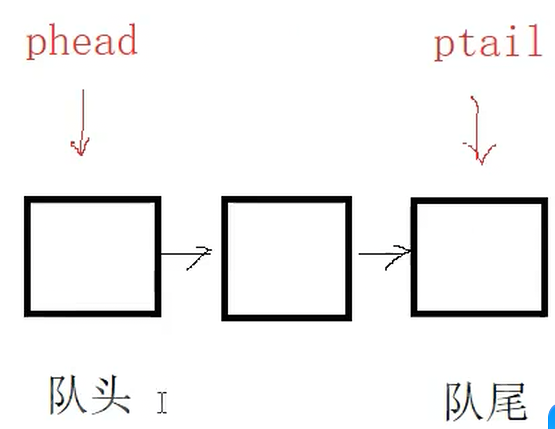
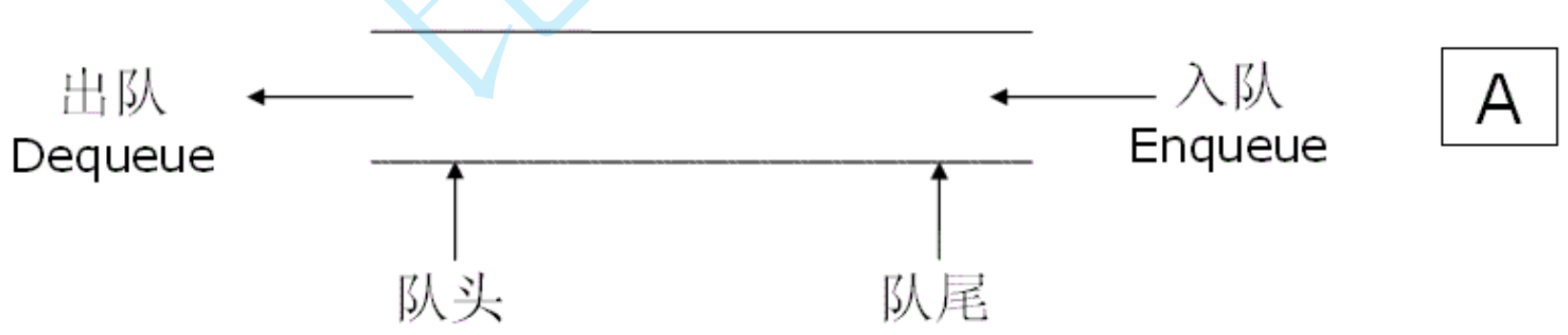
    概念：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出的特点。

    入队列：进行插入操作的一端称为队尾。

    出队列：进行删除操作的一端称为队头。

3.2 队列底层结构选型

     队列也可以用数组或者链表的结构实现，但是哪种结构更优呢？

3.2.1 数组评估（时间复杂度）

   ①队尾插入数据：时间复杂度为O(1)。

   ②队头删除数据：时间复杂度为O(N)。

3.2.1 链表（单链表）评估（时间复杂度）

   ①队尾插入数据：时间复杂度为O(N)。

   ②队头删除数据：时间复杂度为O(1)。

    但是嗷，我们不仅学了单链表，还学了双链表，如果用双链表的话，不管是在头部删除还是尾部插入，时间复杂度都是O（1），由此可见，目前用双链表来实现队列是可行的。但是：如果用双链表的话，每次得申请一整个节点，而这一整个节点包括：int类型的数据，前驱指针和后继指针（总共需要3*4=12个节点）如此说来，双链表比较消耗空间，所以，我们一般不轻易用双链表来实现栈或者队列，因为用它来解决问题成本会更高。

    那根据前面对二者的讨论可以发现，无论是数组还是单链表，队尾插入和队头删除，都不能实现两全其美，使其时间复杂度与空间复杂度均为O（1），但是我们可以对数组或者单链表进行优化，使其各自的时间复杂度和空间复杂度均变成O(1)呢？我们继续思考，到底是使用数组还是双链表来实现呢？

    用数组实现队头删除数据的时间复杂度永远为O(N)，不能优化成O（1），用单链表队尾插入数据的时间复杂度为O(N)，但此时我们可以再定义一个ptail指针指向尾节点，然后再插入数据，此时单链表队尾插入数据的时间复杂度就变成O（1）了。

    综上，用单链表（单链表+额外的ptail指针）可以更好的实现队列，用其实现成本会更低一些。

3.3 队列的实现

3.3.1 定义队列的结构

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
//定义一个节点结构
typedef int QDataType;
typedef struct QueueNode {QDataType data;struct QueueNode* next;
}QueueNode;
//定义队列的结构
typedef struct Queue {QueueNode* phead;//队头QueueNode* ptail;//队尾
}Queue;

3.2.2 队列的初始化

#include "Queue.h"
//1.初始化
void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;
}
#include "Queue.h"
void test01()
{Queue q;QueueInit(&q);
}
int main()
{test01();return 0;
}

 3.2.3 入队

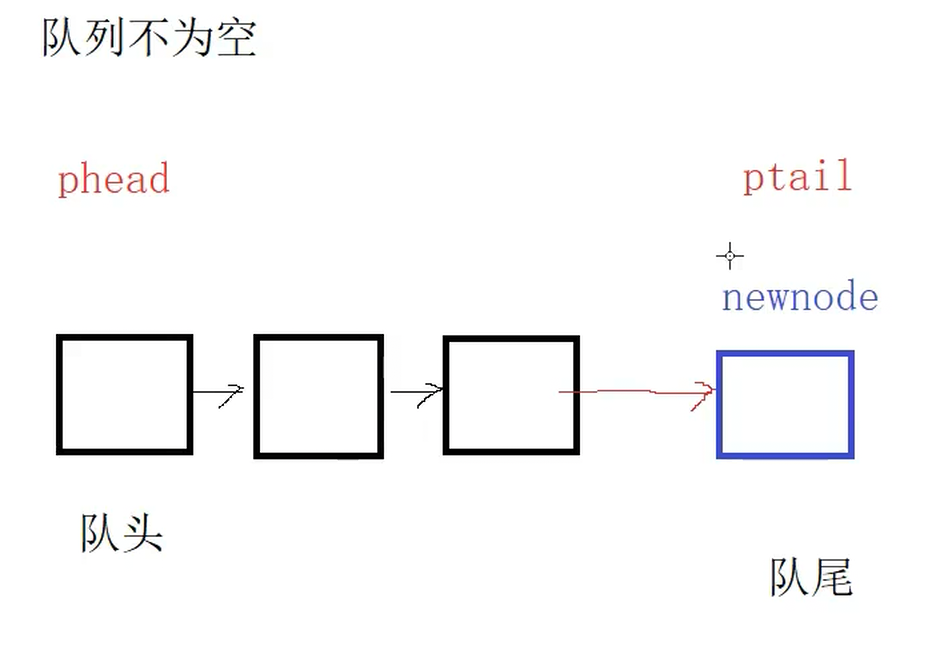   和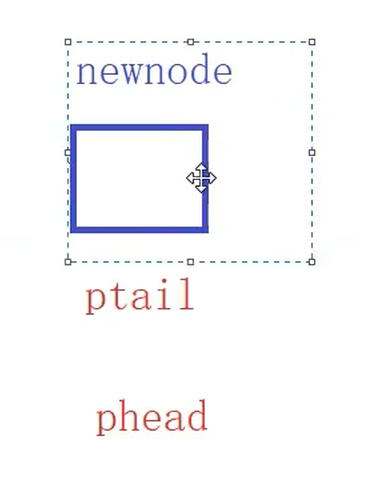

//2.入队
void QueuePush(Queue* pq, QDataType x)
{assert(pq);//创建值为x的节点QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail!");exit(1);}newnode->data = x;newnode->next = NULL;//如果队列为空if (pq->phead == NULL){pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = pq->ptail->next;}
}

3.2.4 出队

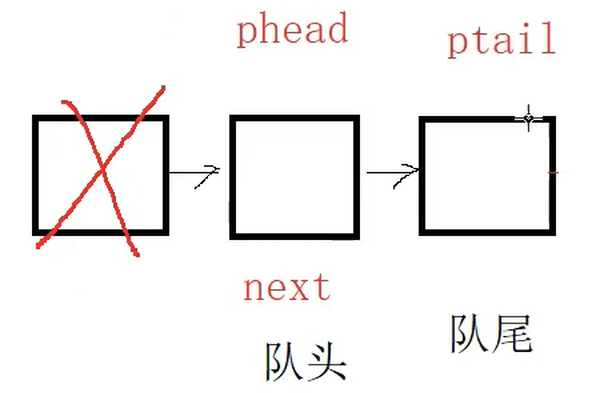   和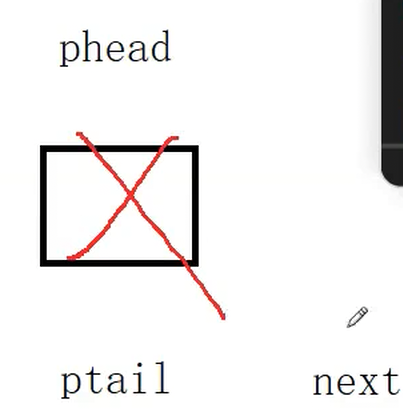        

//4.出队
void QueuePop(Queue* pq)
{assert(!QueueEmpty(&pq));//队列中只有一个节点时if (pq->phead->next == NULL)  //括号里也可以写pq->phead==pq->ptail{free(pq->phead);pq->phead = pq->ptail = NULL;}else{QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}
}

3.2.5 取队头和队尾数据

//5.取队头数据
QDataType QueueFront(Queue* pq)
{assert(!QueueEmpty(&pq));return pq->phead->data;
}
//6.取队尾数据
QDataType QueueBack(Queue* pq)
{assert(!QueueEmpty(&pq));return pq->ptail->data;
}

3.2.6 队列中有效元素个数

//7.获取队列元素有效个数
int QueueSize(Queue* pq)
{assert(pq);int count = 0;QueueNode* pcur = pq->phead;while (pcur){count++;pcur = pcur->next;}return count;
}

    我们发现，除了“获取队列中有效元素个数”，其余的功能实现时间复杂度都是O（1），就只有这个时间复杂度为O(N),那有什么办法可以使其时间复杂度为O(1)呢？

    可以在定义队列结构中声明size，这样就不用遍历了，可以直接返回size。

//7.获取队列元素有效个数
int QueueSize(Queue* pq)
{assert(pq);/*int count = 0;QueueNode* pcur = pq->phead;while (pcur){count++;pcur = pcur->next;}return count;*/return pq->size;
}

3.2.7 队列的销毁

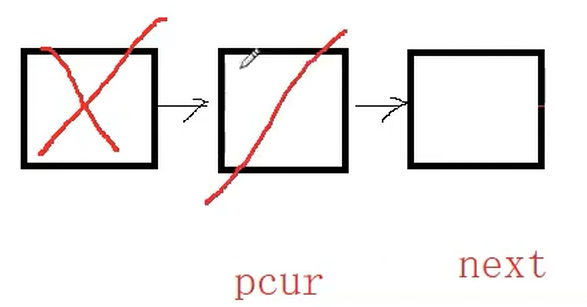
//8.销毁队列
void QueueDestory(Queue* pq)
{assert(pq);QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = pcur->next;}pq->phead = pq->ptail = NULL;
}

四. 所有代码如下：

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
//定义一个节点结构
typedef int QDataType;
typedef struct QueueNode {QDataType data;struct QueueNode* next;
}QueueNode;
//定义队列的结构
typedef struct Queue {QueueNode* phead;//队头QueueNode* ptail;//队尾int size;//有效元素个数
}Queue;//1.初始化
void QueueInit(Queue* pq);
//2.入队
void QueuePush(Queue* pq, QDataType x);
//3.判断队列是否为空
bool QueueEmpty(Queue* pq);
//4.出队
void QueuePop(Queue* pq);
//5.取队头数据
QDataType QueueFront(Queue* pq);
//6.取队尾数据
QDataType QueueBack(Queue* pq);
//7.获取队列元素有效个数
int QueueSize(Queue* pq);
//8.销毁队列
void QueueDestory(Queue* pq);
#include "Queue.h"
//1.初始化
void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;
}
//2.入队
void QueuePush(Queue* pq, QDataType x)
{assert(pq);//创建值为x的节点QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail!");exit(1);}newnode->data = x;newnode->next = NULL;//如果队列为空if (pq->phead == NULL){pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = pq->ptail->next;}
}
//3.判断队列是否为空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL;
}
//4.出队
void QueuePop(Queue* pq)
{assert(!QueueEmpty(&pq));//队列中只有一个节点时if (pq->phead->next == NULL)  //括号里也可以写pq->phead==pq->ptail{free(pq->phead);pq->phead = pq->ptail = NULL;}else{QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}
}
//5.取队头数据
QDataType QueueFront(Queue* pq)
{assert(!QueueEmpty(&pq));return pq->phead->data;
}
//6.取队尾数据
QDataType QueueBack(Queue* pq)
{assert(!QueueEmpty(&pq));return pq->ptail->data;
}
//7.获取队列元素有效个数
int QueueSize(Queue* pq)
{assert(pq);/*int count = 0;QueueNode* pcur = pq->phead;while (pcur){count++;pcur = pcur->next;}return count;*/return pq->size;
}
//8.销毁队列
void QueueDestory(Queue* pq)
{assert(pq);QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = pcur->next;}pq->phead = pq->ptail = NULL;
}

以上就是今天的内容，感兴趣的小伙伴可以一键三连哦~

http://www.dtcms.com/a/473408.html

相关文章：

  • ros2系统在ubuntu18.04环境下的环境搭建
  • 个人网站展示dw网站制作
  • 鸿蒙NEXT系列之精析NDK UI API（节点增删和属性设置）
  • 10个免费货源网站郑州网络科技公司有哪些
  • Spring 源码学习（十三）—— RequestMappingHandlerAdapter
  • 虚幻引擎虚拟制片入门教程 之 3D渲染基础知识：模型、材质、贴图、UV等
  • excel导出使用arthas动态追踪方法调用耗时后性能优化的过程
  • 【数据结构】强化训练：从基础到入门到进阶（2）
  • python异步编程 -什么是python的异步编程， 与多线程和多进程的区别
  • Linux系统--进程间通信--共享内存相关指令
  • 网站开发的实践报告石家庄市工程勘察设计咨询业协会
  • TensorFlow深度学习实战——图分类
  • SAP MM采购信息记录维护接口分享
  • 网站搭建装修风格大全2021新款简约
  • Mysql初阶第八讲：Mysql表的内外连接
  • SpringCloud 入门 - Gateway 网关与 OpenFeign 服务调用
  • uniapp 选择城市（城市列表选择）
  • AR小白入门指南：从零开始开发增强现实应用
  • 02_k8s资源清单
  • 2025年渗透测试面试题总结-109（题目+回答）
  • uniapp配置自动导入uni生命周期等方法
  • flink的Standalone-HA模式安装
  • Flink时态表关联：实现数据“时间旅行”的终极方案
  • 做哪类英文网站赚钱wordpress 页面 列表
  • nginx + spring cloud + redis + mysql + ELFK 部署
  • 【黑马点评 - 实战篇01】Redis项目实战（Windows安装Redis6.2.6 + 发送验证码 + 短信验证码登录注册 + 拦截器链 - 登录校验）
  • 汕头市通信建设管理局网站二网站手
  • FreeRTOS小记
  • 数据结构实战：顺序表全解析 - 从零实现到性能分析
  • 【C++进阶】继承上 概念及其定义 赋值兼容转换 子类默认成员函数的详解分析