基于螳螂虾优化的LSTM深度学习网络模型(MShOA-LSTM)的一维时间序列预测算法matlab仿真
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.部分程序
4.算法理论概述
5.完整程序
1.程序功能描述
基于螳螂虾优化的LSTM(MShOA-LSTM)算法是仿生优化算法与深度学习模型的融合创新,核心解决传统LSTM超参数人工调试导致的收敛慢、精度低问题。其架构包含两大模块:
预测主体:LSTM 网络,通过门控机制捕捉时间序列的长短期依赖关系;
优化引擎:螳螂虾优化算法(MShOA),模拟螳螂虾视觉感知与行为策略,实现LSTM关键超参数的全局寻优。
算法流程遵循 "超参数优化→模型训练→时序预测" 的闭环:先通过MShOA优化LSTM的隐藏层神经元数、学习率等核心参数,再用最优参数构建模型并训练,最终输出时间序列预测结果。该融合架构在电力负荷、传感器数据等一维时序场景中,可显著提升预测精度与模型鲁棒性。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
3.部分程序
..........................................................................
[~,I]=min(VV);
% 将优化得到的最佳参数转换为整数,作为LSTM隐藏层神经元数量
% 加1是为了确保至少有1个神经元
NN=floor(Positions(I,:))+1;
% 定义LSTM神经网络结构
% 设置网络训练参数
options = trainingOptions('adam', ... % 使用Adam优化器,适合深度学习训练'MaxEpochs', 240, ... % 最大训练轮数为240'GradientThreshold', 1, ... % 梯度阈值为1,防止梯度爆炸'InitialLearnRate', 0.004, ... % 初始学习率为0.004'LearnRateSchedule', 'piecewise', ...% 学习率调度方式为分段衰减'LearnRateDropPeriod', 60, ... % 每60轮衰减一次学习率'LearnRateDropFactor',0.2, ... % 学习率衰减因子为0.2(变为原来的20%)'L2Regularization', 0.01, ... % L2正则化系数为0.01,防止过拟合'ExecutionEnvironment', 'gpu',... % 使用GPU加速训练(需配置GPU支持)'Verbose', 0, ... % 不显示训练过程细节'Plots', 'training-progress'); % 显示训练进度图表(损失变化等)% 训练LSTM网络
[net,INFO] = trainNetwork(Pxtrain, Txtrain, layers, options);% 使用训练好的网络进行预测
Dat_yc1 = predict(net, Pxtrain); % 对训练数据进行预测(归一化尺度)
Dat_yc2 = predict(net, Pxtest); % 对测试数据进行预测(归一化尺度)% 将预测结果反归一化,恢复到原始数据范围
Datn_yc1 = mapminmax('reverse', Dat_yc1, Norm_O);
Datn_yc2 = mapminmax('reverse', Dat_yc2, Norm_O); % 将细胞数组转换为矩阵(方便后续处理和分析)
Datn_yc1 = cell2mat(Datn_yc1);
Datn_yc2 = cell2mat(Datn_yc2);% 保存训练信息、预测结果和收敛曲线到MAT文件,便于后续分析
save R2.mat INFO Datn_yc1 Datn_yc2 T_train T_test Convergence_curve
1184.算法理论概述
传统LSTM的超参数依赖人工调试,存在两大问题:
局部最优陷阱:随机初始化参数易导致模型收敛于局部最小值,预测误差偏高;
收敛效率低:学习率过大易震荡,过小则收敛缓慢,尤其在长序列数据中表现明显。
MShOA是2025年提出的新型群智能优化算法,灵感源于螳螂虾的视觉感知与行为策略,具备全局寻优能力强、收敛速度快的特点,为LSTM超参数优化提供理想引擎。
螳螂虾拥有地球最复杂的视觉系统,可识别偏振光并据此执行三大行为:随机觅食、猎物攻击、藏身防御,MShOA将其转化为三层优化策略:

MShOA的优化过程分为初始化、偏振类型判断、行为策略执行三大步骤,核心数学公式如下:


(3)三大优化策略的数学表达
根据PTI值执行对应策略,实现个体位置(超参数组合)的迭代更新:
觅食策略(PTI=1):模拟布朗运动的随机搜索,扩大寻优范围
![]()
攻击策略(PTI=2):模拟圆周打击的局部开发,精准逼近最优解

防御策略(PTI=3):模拟藏身的收缩搜索,避免过度探索

适应度函数设计
MShOA以LSTM的预测误差为适应度,目标是最小化误差函数:
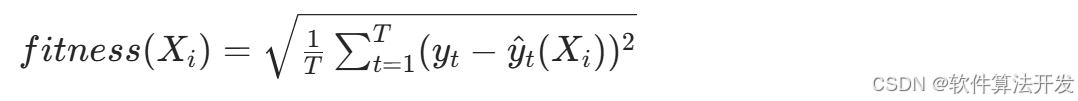
基于MShOA优化得到的最优参数Xbest∗,构建并训练最终的LSTM模型。
相比传统LSTM,MShOA-LSTM的优势可通过收敛性与精度指标量化:
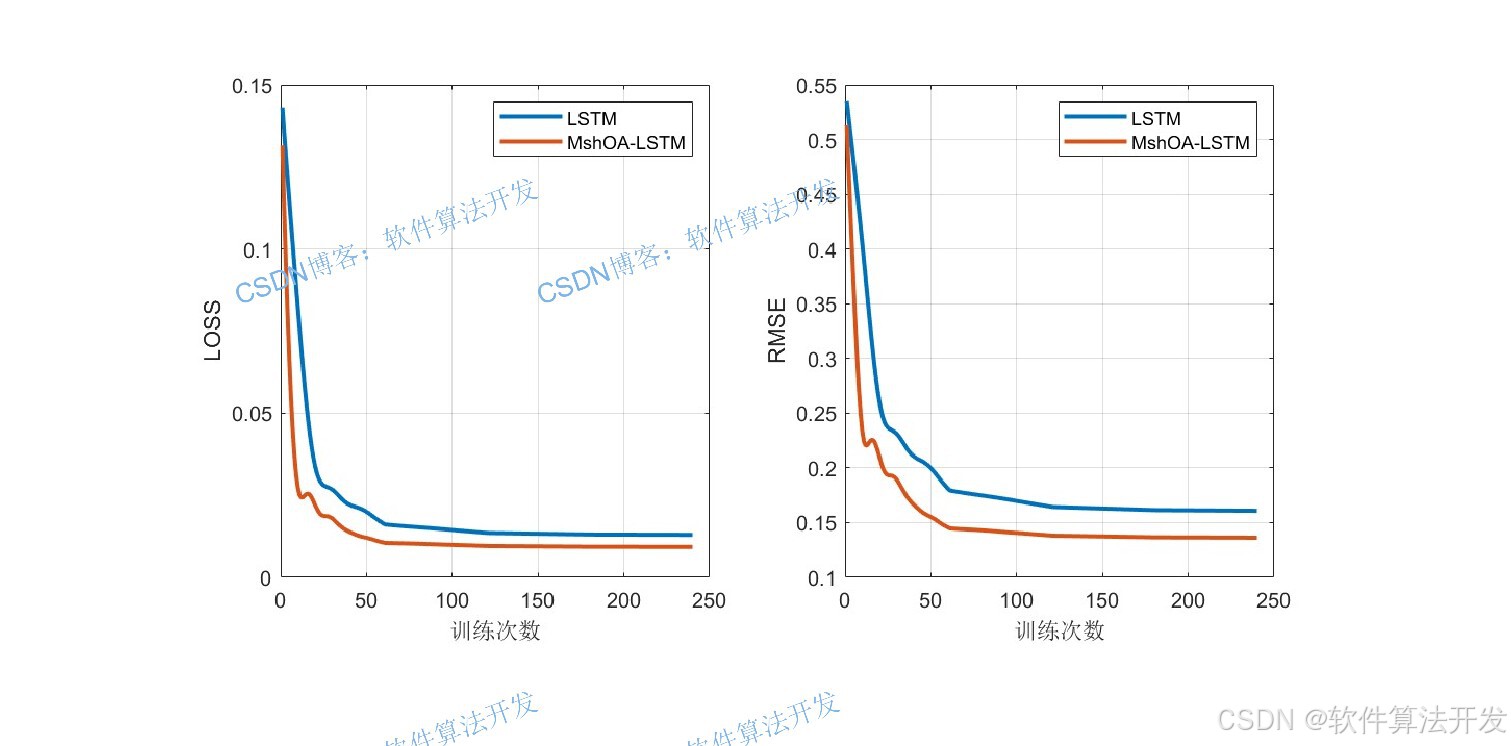
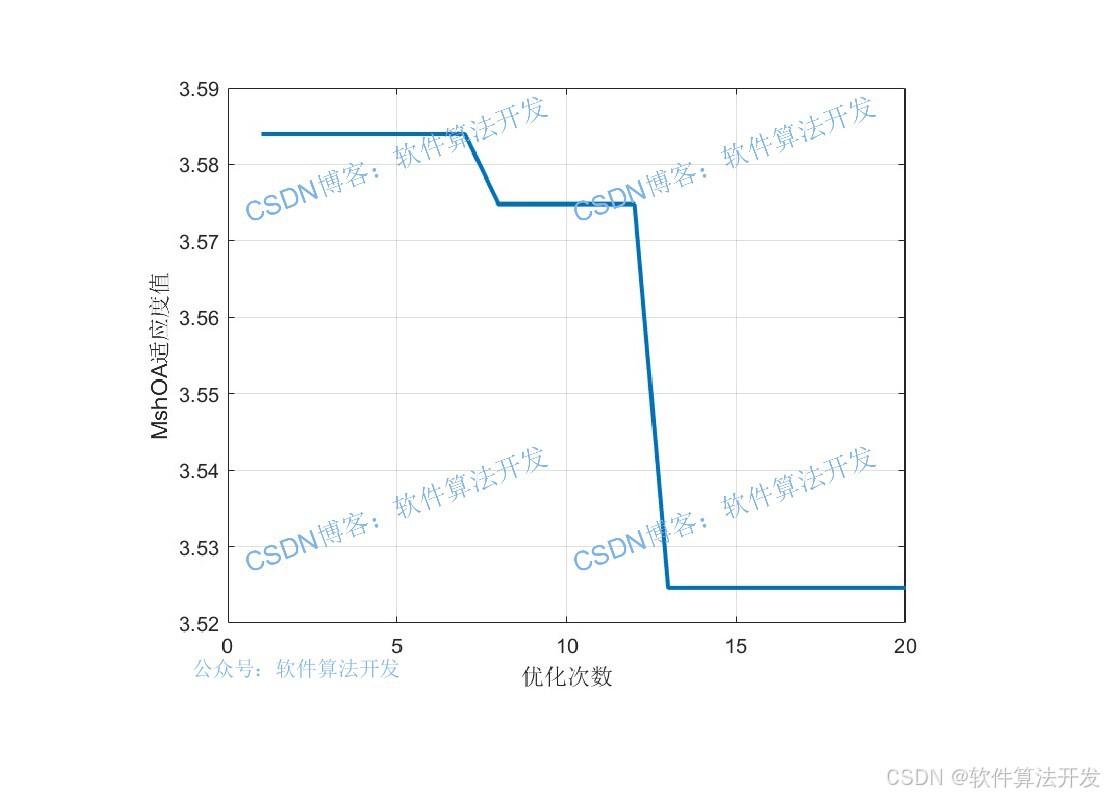
收敛速度:MShOA的攻击策略使超参数快速逼近最优值,收敛迭代次数减少10%以上。
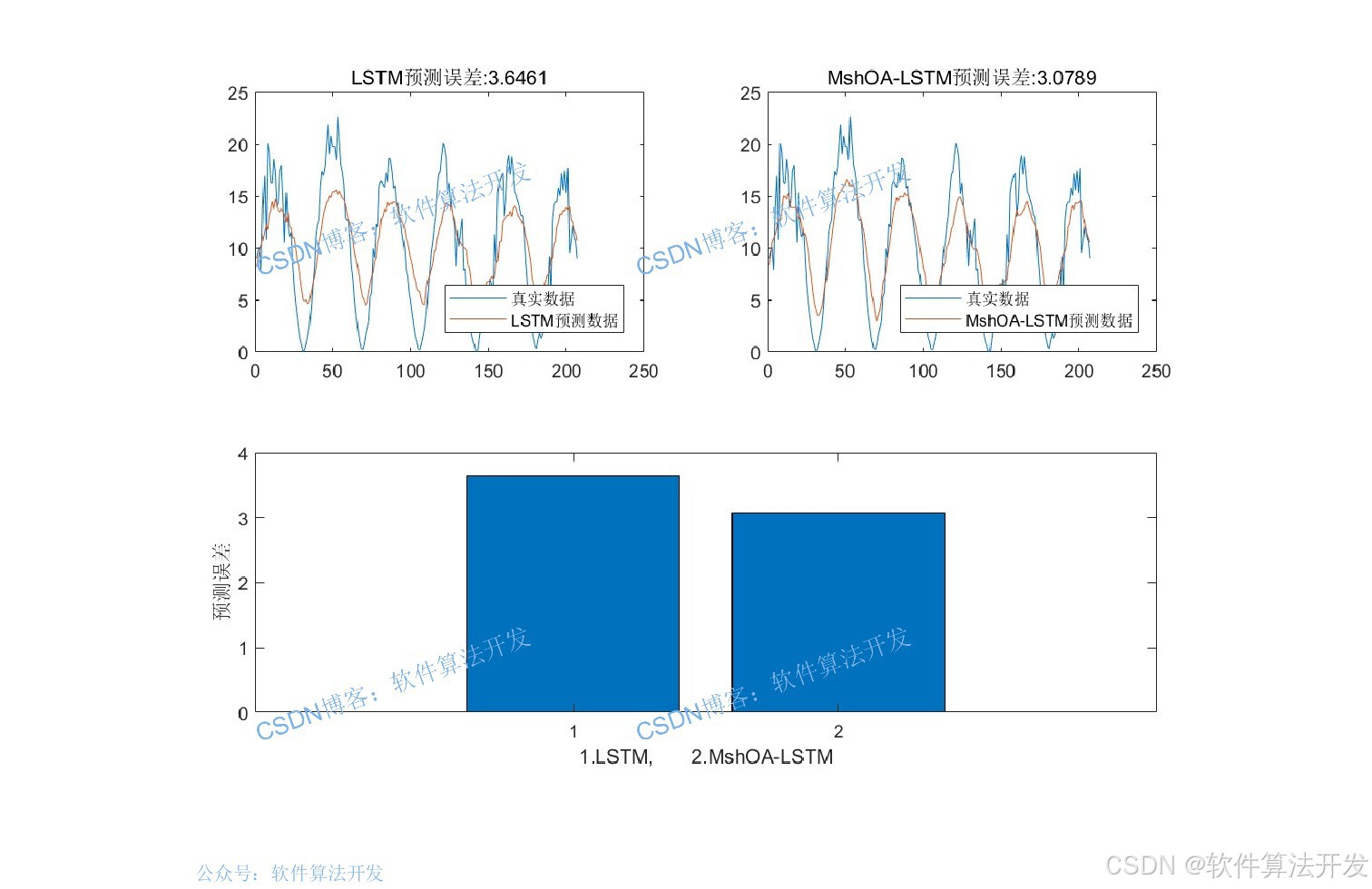
预测精度:最优超参数组合使LSTM的均方根误差(RMSE)降低20%。
5.完整程序
VVV
关注后手机上输入程序码:118
