LeetCode算法日记 - Day 67: 不同路径、最长递增子序列

目录

1. 不同路径

1.1 题目解析

1.2 解法

1.3 代码实现

2. 最长递增子序列

2.1 题目解析

2.2 解法

2.3 代码实现

---

1. 不同路径

https://leetcode.cn/problems/unique-paths/description/

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

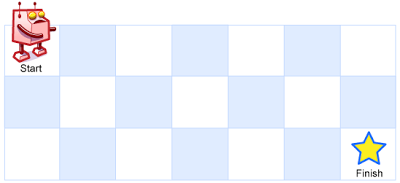
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

1.1 题目解析

题目本质
这是一个路径计数问题，本质是"在约束条件下（只能向右或向下）从起点到终点有多少种走法"。每个位置的路径数等于"能到达该位置的所有前驱位置的路径数之和"。

常规解法
最直观的想法是用DFS暴力搜索——从起点(0,0)开始，每次尝试向右或向下走，到达终点就计数+1。看起来代码简单，直接模拟所有路径。

问题分析
暴力DFS会产生大量重复计算。比如从(0,0)→(1,0)→(1,1)和(0,0)→(0,1)→(1,1)都会重复计算"从(1,1)到终点的路径数"。对于3×3网格，某些位置可能被访问几十次。时间复杂度是O(2^(m+n))，指数级爆炸，m=100时根本算不出来。

思路转折
要想高效 → 必须避免重复计算 → 记忆化搜索或动态规划。关键观察：每个位置的路径数是固定的，只需计算一次。可以用备忘录缓存结果，或者反向思考——从终点往起点推导，利用"到达(i,j)的路径数 = 到达(i-1,j)的路径数 + 到达(i,j-1)的路径数"这个递推关系。这样每个位置只计算一次，复杂度降到O(m×n)。

1.2 解法

算法思想
记忆化递归（自顶向下的DP）。从终点(m,n)开始递归，逆向推导到起点(1,1)。核心递推公式：

f(i, j) = f(i-1, j) + f(i, j-1)
f(1, 1) = 1  （起点到起点，1条路径）
f(i, 0) = 0, f(0, j) = 0  （越界，0条路径）

i）初始化备忘录：创建memo数组，全部填充-1表示未计算

ii）定义递归函数：unique(i, j)表示从(1,1)到(i,j)有多少条路径

iii）递归终止条件：

• 到达起点(1,1)，返回1

• 越界(i=0或j=0)，返回0

iv）查表优化：如果memo[i][j]已计算，直接返回

v）递推计算：memo[i][j] = unique(i-1, j) + unique(i, j-1)

vi）调用入口：unique(m, n)

易错点

• 索引混淆：代码用1-indexed（起点是(1,1)），但Java数组是0-indexed。memo[i][j]对应网格位置(i,j)而非数组下标，注意边界判断用si==0而非si<0

• 备忘录大小：题目说m,n最大100，但代码直接开memo[101][101]，这样1-indexed时memo[100][100]刚好可用。如果开memo[100][100]会越界

• 越界判断顺序：必须先判断si==0||sj==0返回0，再判断memo查表，否则memo[-1][j]会数组越界

• 递归方向理解：这是从终点往起点推，不是从起点往终点走。unique(m,n)表示"起点到(m,n)的路径数"，通过拆解成"到(m-1,n)的路径数 + 到(m,n-1)的路径数"来计算

1.3 代码实现

class Solution {int m, n;int[][] memo;public int uniquePaths(int _m, int _n) {m = _m;n = _n;memo = new int[101][101];  // 1-indexed，开101避免越界for (int i = 0; i < memo.length; i++) {Arrays.fill(memo[i], -1);  // -1表示未计算}   return unique(m, n);}public int unique(int si, int sj) {// 边界条件：到达起点if (si == 1 && sj == 1) return 1;// 越界：超出网格边界if (si == 0 || sj == 0) return 0;// 查表：已计算过if (memo[si][sj] != -1) return memo[si][sj];// 递推：当前位置路径数 = 上方路径数 + 左方路径数memo[si][sj] = unique(si - 1, sj) + unique(si, sj - 1);return memo[si][sj];}
}

复杂度分析

• 时间复杂度：O(m × n)。每个位置最多计算一次，共m×n个位置。

• 空间复杂度：O(m × n)。备忘录数组O(m×n)，递归栈深度最坏O(m+n)，总体O(m×n)。

2. 最长递增子序列

https://leetcode.cn/problems/longest-increasing-subsequence/description/

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

进阶：

• 你能将算法的时间复杂度降低到 O(n log(n)) 吗?

2.1 题目解析

题目本质
在数组中找到一个最长的子序列，要求子序列中的元素严格递增。这是一个经典的"决策累积型"问题——每个元素都要决策"选或不选"，最终累积出最优解。

常规解法
最直观的想法是枚举所有可能的子序列，检查哪些是严格递增的，然后找出最长的那个。可以用递归来实现：对每个位置决定选或不选。

问题分析
暴力枚举的时间复杂度是O(2^n)，因为每个元素都有选/不选两种状态。当数组长度达到2500时，这个复杂度完全不可接受。问题在于存在大量重复计算——同样的"位置+前一个选择的元素"状态会被反复计算。

思路转折
要想高效 → 必须避免重复计算 → 记忆化搜索。核心是定义状态：dfs(pos, prev) 表示"从位置pos开始，前一个选择的元素索引为prev时，能获得的最长递增子序列长度"。通过memo数组缓存计算结果，将指数级复杂度降到多项式级。

2.2 解法

算法思想

使用DFS + 记忆化搜索，状态定义为 dp[pos][prev]，表示从位置 pos 开始、前一个选择元素的索引为 prev 时的最长递增子序列长度。

递推关系：

dp[pos][prev] = max(不选当前元素, 选当前元素)
- 不选：dp[pos+1][prev]
- 选（需满足 nums[pos] > nums[prev]）：dp[pos+1][pos] + 1

i）初始化：创建 memo[n][n+1] 数组，全部填充为 -1 表示未计算。注意第二维是 n+1，因为 prev 的取值范围是 [0, n]。

ii）DFS递归：从位置0开始，初始 prev 设为 n（表示还未选择任何元素）。

• 递归边界：pos == n 时返回 0（已遍历完所有元素）

• 如果该状态已计算过，直接返回缓存值

iii）决策分支：

• 不选当前元素：直接递归 dfs(pos+1, prev)

• 选当前元素：需满足 prev == n（还没选过元素）或 nums[pos] > nums[prev]（严格递增），递归 dfs(pos+1, pos) + 1

iv）记忆化：取两种决策的最大值，存入 memo[pos][prev] 并返回。

易错点

• prev 的特殊标记值：使用 n 作为"尚未选择任何元素"的标记。因为数组索引范围是 [0, n-1]，n 是一个永远不会在正常遍历中出现的值，避免了与实际索引冲突。这就是为什么 memo 的第二维要开到 n+1。

• 数组维度：memo[n][n+1] 而非 memo[n][n]，因为 prev 可以取到 n。

• 严格递增条件：判断条件是 nums[pos] > nums[prev] 而不是 >=，确保子序列严格递增。

2.3 代码实现

class Solution {int n;int[][] memo;public int lengthOfLIS(int[] nums) {n = nums.length;memo = new int[n][n+1];  // prev可以取到n，所以是n+1for(int[] row : memo) {Arrays.fill(row, -1);  // 初始化为-1表示未计算}return dfs(nums, 0, n);  // 从位置0开始，prev=n表示还没选过元素}public int dfs(int[] nums, int pos, int prev){if(pos == n) return 0;  // 遍历结束，返回0if(memo[pos][prev] != -1) return memo[pos][prev];  // 已计算过// 不选当前元素int noTake = dfs(nums, pos+1, prev);// 选当前元素（需满足严格递增条件）int take = 0;if(prev == n || nums[pos] > nums[prev]){take = dfs(nums, pos+1, pos) + 1;}// 取最大值并记忆化memo[pos][prev] = Math.max(take, noTake);return memo[pos][prev];}
}

复杂度分析

• 时间复杂度：O(n²)。状态总数为 n × (n+1)，每个状态计算一次，每次计算O(1)。

• 空间复杂度：O(n²)。memo 数组占用 n × (n+1) 的空间，递归调用栈深度为O(n)。