当前位置：首页 > news >正文

「机器学习笔记9」回归分析：从理论到实践的全面指南

news 2025/10/11 8:39:09

什么是回归分析

回归分析是一种描述变量间关系的统计分析方法，通过建立数学模型来探索数据中的规律性。在现代机器学习中，回归分析扮演着至关重要的角色。

在线教育场景中，我们可以将课程满意度作为因变量Y，而将平台交互性、教学资源质量和课程设计作为自变量X。通过回归分析，我们能够量化这些因素对学生满意度的具体影响程度。

回归分析本质上是一种预测性建模技术，主要用于预测分析。虽然预测结果多为连续值，但它也可以用于预测离散值甚至二值结果。

线性回归：简单却强大

线性回归是回归分析中最基础的形式，它假设因变量和自变量之间存在线性关系。这种关系的直观表现可以用一条直线来刻画，而线性回归的目的就是找到最能匹配数据的截距和斜率。

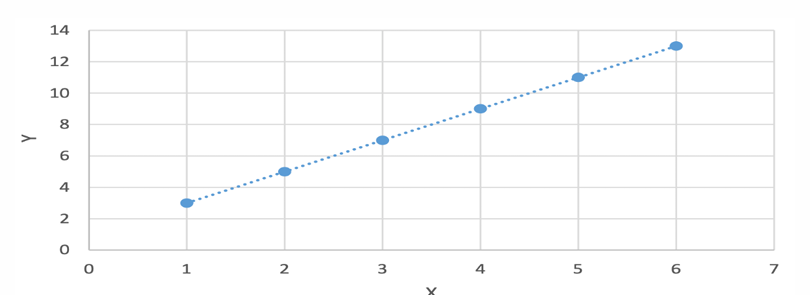
在某些情况下，变量间的线性关系是确定性的，比如当X取值1、2、3、4、5、6时，Y对应取值3、5、7、9、11、13。然而在实际应用中，变量间通常只是近似的线性关系，这就需要我们找到一条能够最好地解释数据的直线。

如何拟合数据

假设只有一个因变量和自变量，每个训练样例表示(𝑥𝑖,𝑦𝑖)
用 $y^i\hat{y}_i$ 表示根据拟合直线和x𝑖 对𝑦𝑖 的预测值 $y^i=b1+b2xi\hat{y}_i=b_1+b_2x_i$
定义 $e𝑖=𝑦𝑖−y^ie𝑖_ =𝑦_𝑖− \hat{y}_i$ 为误差项

目标：得到一条直线使得对于所有训练样例的误差项尽可能小

线性回归的基本假设

为了确保线性回归模型的有效性，我们需要满足以下四个基本假设：

线性关系假设：自变量与因变量间存在线性关系
独立性假设：数据点之间相互独立
无共线性假设：自变量之间无高度相关性，相互独立
正态性假设：残差独立、等方差，且符合正态分布

这些假设是线性回归模型成立的基础，在实际应用中需要通过各种统计检验来验证这些假设是否得到满足。

损失函数：衡量模型好坏的标准

在回归分析中，损失函数用于量化预测值与真实值之间的差异。常见的损失函数包括：

所有误差项的加和： $∑i=1nei=∑i=1n(yi−yi^)\sum_{i=1}^n e_i = \sum_{i=1}^n(y_i-\hat{y_i})$
所有误差项绝对值的加和： $∑i=1n∣ei∣=∑i=1n∣(yi−yi^)∣\sum_{i=1}^n |e_i| = \sum_{i=1}^n|(y_i-\hat{y_i})|$

然而最常用的是基于误差平方和的损失函数，因为它具有良好的数学性质且便于优化。

$min⁡b1,b2∑i=1nei2=∑i=1n(yi−y^i)2=∑i=1n(yi−b1−b2xi)2 \begin{aligned} \min_{b_{1}, b_{2}} \sum_{i=1}^{n} e_{i}^{2} &= \sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^{2} \\ &= \sum_{i=1}^{n} (y_{i} - b_{1} - b_{2} x_{i})^{2} \end{aligned}$

最小二乘法：求解最优参数

最小二乘法是一种凸优化方法，用于求解最优的截距和斜率参数。通过最小化误差平方和，我们可以得到最佳的参数估计值。

具体求解过程中，我们需要计算自变量和因变量的均值，然后通过公式计算斜率参数。这种方法保证了我们得到的解是全局最优解，而非局部最优。

对误差平方和分别求偏导并令其为零：

$\frac{\partial \sum_{i=1}^{n} e_{i}^{2}}{\partial b_{1}} = -2\sum_{i=1}^{n} \left(y_{i}-b_{1}-b_{2} x_{i}\right) = 0 \tag{1}$

$\frac{\partial \sum_{i=1}^{n} e_{i}^{2}}{\partial b_{2}} = -2\sum_{i=1}^{n} x_{i}\left(y_{i}-b_{1}-b_{2} x_{i}\right) = 0 \tag{2}$

参数估计解

求解上述正规方程组得到回归系数估计量：

$b_{2} = \frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}$

$b_{1} = \bar{y} - b_{2}\bar{x}$

其中：

$b_1$ 为截距项估计量
$b_2$ 为斜率项估计量
$xˉ=1n∑i=1nxi\bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i$ 为自变量样本均值
$yˉ=1n∑i=1nyi\bar{y} = \frac{1}{n}\sum_{i=1}^{n} y_i$ 为因变量样本均值
$n$ 为样本容量

梯度下降法：迭代优化的艺术

除了最小二乘法，梯度下降法提供了另一种参数求解途径。这种方法通过迭代更新参数值，逐步逼近最优解。

梯度下降法的核心思想是沿着损失函数的负梯度方向更新参数。初始化参数值后，重复以下步骤直到收敛：计算梯度，然后按照学习率调整参数值。

算法步骤

初始化 $b_1, b_2$ , 可以通过random随机初始化
重复：
- $b1=b1−αb_1 = b_1 - \alpha$
- $b2=b2−αb_2 = b_2 - \alpha$

简单示例：

import numpy as np
# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1) # 真实关系: y = 4 + 3x + 噪声# 初始化参数 (对应您图片中的 b1, b2，这里我们用 w 和 b)
w = np.random.randn(1) # 权重，可以理解为b1
b = np.zeros(1)        # 偏置，可以理解为b2# 设置超参数
learning_rate = 0.1    # 学习率 α
n_iterations = 1000    # 最大迭代次数# 梯度下降开始
for i in range(n_iterations):# 1. 计算预测值y_pred = w * X + b# 2. 计算损失（MSE），用于监控loss = np.mean((y_pred - y)**2)if i % 100 == 0:print(f"Iteration {i}: Loss = {loss:.4f}")# 3. 计算梯度！（这是图片中缺失的关键步骤）# 损失函数 J 对 w 的偏导数dw = (2 / len(X)) * np.sum((y_pred - y) * X)# 损失函数 J 对 b 的偏导数db = (2 / len(X)) * np.sum(y_pred - y)# 4. 同时更新参数 w 和 b！（对应图片中的更新步骤，但补全了梯度项）w = w - learning_rate * dwb = b - learning_rate * db
# 输出最终结果
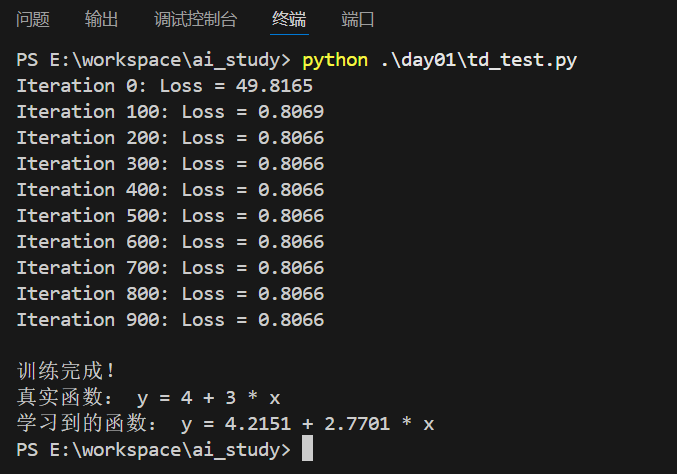
print(f"\n训练完成！")
print(f"真实函数： y = 4 + 3 * x")
print(f"学习到的函数： y = {b[0]:.4f} + {w[0]:.4f} * x")

执行结果:

这种方法特别适用于大规模数据集和在线学习场景，因为它可以逐样本更新模型参数。

多元线性回归：处理复杂关系

当因变量有多个时，我们需要使用多元线性回归。这时矩阵表示法就显得格外重要。

多元线性回归的矩阵表示为：Y=Xβ+ϵ

参数估计的推导(法一）

此时误差项向量 e 定义为真实值 y 与预测值 Xβ 的差值：

$\begin{bmatrix} e_{1} \\ e_{2} \\ \vdots \\ e_{n} \end{bmatrix} = y - X \beta$

损失函数定义为所有误差项的平方和（Sum of Squared Errors, SSE），它可以简洁地用向量转置表示为：

$\sum_{i=1}^{n} e_{i}^{2} = e'e$

（其中 $e^{'}$ 表示向量 $e$ 的转置）

求解最小二乘估计
为了找到使损失函数最小的参数 $β\beta$ ，我们对其求导并令导数为零：

$\frac{\partial e' e}{\partial \beta} = -2 X' Y + 2 X' X \beta = 0$

解析解（正规方程）
通过求解上述方程，可以得到参数 $β\beta$ 的最优解，即著名的正规方程：

$\beta = (X' X)^{-1} X' Y$

其中Y是因变量向量，X是自变量矩阵，β是系数向量，ε是误差项。基于这种表示，损失函数可以写为误差平方和的形式。

通过求解正规方程，我们可以得到系数的最优估计：β=(X′X)−1X′Y

参数估计的推导(法二）

1. 问题定义与目标

用一组参数 $β0,β1,…,βk\beta_0, \beta_1, \dots, \beta_k$ 来拟合因变量 $y$ ，模型形式如下：

$y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_k x_{ik} + \epsilon_i$

其中：

$y_i$ 是第 $i$ 个观测的因变量值。
$x_{i1}, ..., x_{ik}$ 是第 $i$ 个观测的自变量值。
$β0\beta_0$ 是截距项。
$β1,...,βk\beta_1, ..., \beta_k$ 是各自变量的系数。
$ϵi\epsilon_i$ 是第 $i$ 个观测无法被模型解释的随机误差。

模型的预测值为：
$y^i=β0+β1xi1+β2xi2+⋯+βkxik \hat{y}_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_k x_{ik}$

第 $i$ 个观测的残差 $e_i$ 为真实值与预测值之差：
$ei=yi−y^i=yi−(β0+β1xi1+⋯+βkxik) e_i = y_i - \hat{y}_i = y_i - (\beta_0 + \beta_1 x_{i1} + \dots + \beta_k x_{ik})$

2. 目标函数：残差平方和（SSE）

普通最小二乘法的目标是找到一组参数 $β\beta$ ，使得所有观测的残差平方和最小。残差平方和定义为：

$\sum_{i=1}^{n} e_{i}^{2} = \sum_{i=1}^{n} (y_{i} - \beta_{0} - \beta_{1} x_{i1} - \dots - \beta_{k} x_{ik})^{2}$

目标：最小化 $SSE(β0,β1,…,βk)\text{SSE}(\beta_0, \beta_1, \dots, \beta_k)$ 。

3. 求解方法：对参数求偏导并令其为0

为了找到最小值点，我们对目标函数（SSE）分别关于每个参数 $βj\beta_j$ 求偏导数，并令其等于零。这会得到一个由 $k + 1$ 个方程组成的方程组（正规方程组）。

偏导过程

对截距项 $β0\beta_0$ 求偏导：
$∂SSE∂β0=−2∑i=1n(yi−β0−β1xi1−⋯−βkxik)=0\frac{\partial SSE}{\partial \beta_0} = -2 \sum_{i=1}^{n} (y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_k x_{ik}) = 0$
化简得：
$\sum_{i=1}^{n} (y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_k x_{ik}) = 0$
对第一个系数 $β1\beta_1$ 求偏导：
$∂SSE∂β1=−2∑i=1n[(yi−β0−β1xi1−⋯−βkxik)⋅xi1]=0\frac{\partial SSE}{\partial \beta_1} = -2 \sum_{i=1}^{n} [(y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_k x_{ik}) \cdot x_{i1}] = 0$
化简得：
$\sum_{i=1}^{n} [(y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_k x_{ik}) \cdot x_{i1}] = 0$
…
对第 $k$ 个系数 $βk\beta_k$ 求偏导：
$∂SSE∂βk=−2∑i=1n[(yi−β0−β1xi1−⋯−βkxik)⋅xik]=0\frac{\partial SSE}{\partial \beta_k} = -2 \sum_{i=1}^{n} [(y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_k x_{ik}) \cdot x_{ik}] = 0$
化简得：
$\sum_{i=1}^{n} [(y_i - \beta_0 - \beta_1 x_{i1} - \dots - \beta_k x_{ik}) \cdot x_{ik}] = 0$

方程组总结：
$\begin{array}{l} \sum (y_{i} - \beta_{0} - \beta_{1} x_{i1} - \dots - \beta_{k} x_{ik}) = 0 \\ \sum (y_{i} - \beta_{0} - \beta_{1} x_{i1} - \dots - \beta_{k} x_{ik}) x_{i1} = 0 \\ \cdots \\ \sum (y_{i} - \beta_{0} - \beta_{1} x_{i1} - \dots - \beta_{k} x_{ik}) x_{ik} = 0 \end{array}$

4. 转化为矩阵形式

为了更简洁地求解，我们将上述方程组用矩阵表示。

定义矩阵和向量：

设计矩阵 $X$ ：在数据矩阵前加一列1，以包含截距项 $β0\beta_0$ 。
$\begin{bmatrix} 1 & x_{11} & \cdots & x_{1k} \\ 1 & x_{21} & \cdots & x_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{nk} \end{bmatrix}_{n \times (k+1)}$
参数向量 $β\beta$ ：
$β=[β0,β1,…,βk]T\beta = [\beta_0, \beta_1, \dots, \beta_k]^T$
因变量向量 $y$ ：
$[y_1, y_2, \dots, y_n]^T$
残差向量 $e$ ：
$[e_1, e_2, \dots, e_n]^T = y - X\beta$

此时，残差平方和可以写为：
$e^Te = (y - X\beta)^T(y - X\beta)$

对方程组 $∑eixij=0\sum e_i x_{ij} = 0$ （对于所有 $j$ ，包括 $x_{i0}=1$ ）进行矩阵化，等价于：
$X^T e = 0$

将 $X\beta$ 代入上式：
$X^T (y - X\beta) = 0$
这被称为正规方程。

5. 推导解析解（闭式解）

由正规方程出发：
$X^T y - X^T X \beta = 0$

移项得：
$X^T X \beta = X^T y$

最后，假设 $X^T X$ 是可逆的（即满秩），我们在等式两边左乘其逆矩阵 $X^T X)^{-1}$ ，即可得到参数向量 $β\beta$ 的最小二乘估计量：

$\beta = (X^T X)^{-1} X^T y$

以“误差平方和”为损失函数的优缺点

用误差平方和作为损失函数有很多优点
- 损失函数是严格的凸函数，有唯一解
- 求解过程简单且容易计算
同时也伴随着一些缺点
- 结果对数据中的“离群点”(outlier)非常敏感
  - 解决方法：提前检测离群点并去除
- 损失函数对于超过和低于真实值的预测是等价的
  - 但有些真实情况下二者带来的影响是不同的

模型评估：相关系数与决定系数

为了评估回归模型的质量，我们引入两个重要指标：

1. 相关系数r：衡量因变量和自变量之间的线性相关程度，计算公式基于协方差和标准差。

$\frac{1}{n - 1} \sum_{i = 1}^{n} \left( \frac{x_{i} - \bar{x}}{s_{x}} \right) \left( \frac{y_{i} - \bar{y}}{s_{y}} \right)$

其中：

$xˉ\bar{x}$ : X 的均值
$s_{x}$ : X 的标准差
$yˉ\bar{y}$ : Y 的均值
$s_{y}$ : Y 的标准差

标准差的计算公式：
$s_x = \sqrt{\frac{1}{n - 1} \sum (x_i - \bar{x})^2}$

2. 决定系数R²：也称为判定系数或拟合优度，计算公式为：

$R2=1−∑i(yi−y^i)2∑i(yi−yˉ)2 R^{2} = 1 - \frac{\sum_{i} (y_{i} - \hat{y}_{i})^{2}}{\sum_{i} (y_{i} - \bar{y})^{2}}$

等价形式
$R2=1−∑i(yi−y^i)2/n∑i(yi−yˉ)2/n=1−MSEVAR R^{2} = 1 - \frac{\sum_{i} (y_{i} - \hat{y}_{i})^{2}/n}{\sum_{i} (y_{i} - \bar{y})^{2}/n} = 1 - \frac{MSE}{VAR}$