分类算法-逻辑回归

​​1. 分类算法的概念​​

分类算法本质上是一种能够依据数据特征进行自动归类的数学模型。我们可以将其理解为一个智能的“分类器”。一个生活中的简单例子是：快递员会综合考量包裹的重量和尺寸，从而将其判断为“大件”或“小件”，这个过程就类似于一个基础的分类任务。

​​2. 逻辑回归概述​​

虽然名称中带有“回归”二字，但逻辑回归（Logistic Regression）主要被应用于解决分类问题。它的核心工作原理是：利用一个数学函数来估算“一个数据点属于某个特定类别的可能性有多大”，这个可能性即是一个介于0和1之间的概率值。最终，算法通过设定一个概率门槛（通常是0.5）来做出分类判断：

• 若计算出的概率值 ​​大于等于 0.5​​，则将该样本判定为 ​​类别1​​。

• 若计算出的概率值 ​​小于 0.5​​，则将其判定为 ​​类别0​​。

​​3. 实战案例：垃圾邮件识别系统​​

​​1. 问题定义与数据观察​​

假设我们需要构建一个垃圾邮件过滤器，其判断依据是邮件的“关键词出现次数”和“邮件正文长度”。我们拥有以下历史数据作为参考：

关键词数量	邮件长度	邮件类别（标签）
10	200	正常邮件 (0)
15	50	垃圾邮件 (1)
5	300	正常邮件 (0)
20	30	垃圾邮件 (1)

从数据中可以观察到一种趋势：关键词多、内容短的邮件更可能被标记为垃圾邮件。

​​2. 数学模型构建​​

逻辑回归模型通过一个特殊的函数（Sigmoid函数）将线性计算的结果映射为概率。其数学表达式为：

P(y=1)=1+e−(w1​x1​+w2​x2​+b)1​

​​公式中各项的含义​​：

• ​​P(y=1)​​：代表邮件是垃圾邮件的预测概率。

• ​​x1​,x2​​​：是输入的特征变量，例如“关键词数量”和“邮件长度”。

• ​​w1​,w2​​​：是模型学习得到的权重，代表了每个特征的重要程度。

• ​​b​​：是偏置项，可以理解为模型的基准调整。

​​3. 模型计算示例​​

假设模型经过训练后，学习到的参数为：

• 权重：w1​=0.3, w2​=−0.01

• 偏置：b=0.5

现在有一封新邮件，其“关键词数量”为18，“邮件长度”为100。我们将其代入模型进行计算：

1. ​​线性加权求和​​：z=w1​x1​+w2​x2​+b=(0.3×18)+(−0.01×100)+0.5=5.4−1+0.5=4.9

2. ​​计算概率值​​：P=1+e−4.91​≈1+0.00741​≈0.993

​​4. 分类决策​​

计算得到的概率 P≈0.993。由于该值远大于预设的阈值0.5，因此模型将这封邮件​​判定为垃圾邮件（类别1）​​。

4. 核心数学原理剖析​​

​​1. 模型假设函数​​

逻辑回归模型的预测核心是 ​​Sigmoid 函数​​，它将线性组合映射到 (0,1) 区间，输出一个概率值。其向量形式的假设函数为：

​​h(x)=P(y=1∣x)=1+e−(wTx+b)1​​​

​​参数说明​​：

• ​​x​​：输入的特征向量。

• ​​w​​：权重向量，每个权重对应一个特征的重要性。

• ​​b​​：偏置项，作为决策边界的一个调整量。

• ​​h(x)​​：模型的输出，表示在给定特征 x的条件下，预测样本属于类别 1 的概率。

​​2. 损失函数：模型训练的衡量标准​​

为了训练模型，我们需要一个函数来衡量预测值 h(x)与真实标签 y之间的差距，这个函数就是损失函数。逻辑回归使用​​对数损失​​。

• ​​概率的统一表达​​：

  为了简洁地表示两种情形的概率，可以将预测正确的概率写为：

  P(y∣x)=[h(x)]y⋅[1−h(x)]1−y

  • 当真实标签 y=1时，公式简化为 P(1∣x)=h(x)。

  • 当真实标签 y=0时，公式简化为 P(0∣x)=1−h(x)。

• ​​极大似然估计​​：

  训练的目标是找到一组参数 (w,b)，使得所有训练样本的预测概率之积最大，即​​似然函数​​最大。通常为了方便计算，我们取其对数，得到​​对数似然函数​​：

  ℓ(w,b)=∑i=1m​[yi​logh(xi​)+(1−yi​)log(1−h(xi​))]

• ​​损失函数​​：

  由于优化算法通常求解最小值，我们将​​负的对数似然函数​​平均化后作为最终的损失函数（也称为交叉熵损失）：

  J(w,b)=−m1​∑i=1m​[yi​logh(xi​)+(1−yi​)log(1−h(xi​))]

  模型训练的目标就是​​最小化​​这个损失函数 J(w,b)。

​​3. 参数学习：梯度下降法​​

我们使用​​梯度下降​​算法来迭代更新参数 w和 b，以寻找使损失函数最小的值。

• ​​梯度计算​​：

  首先需要计算损失函数 J关于每个参数的梯度（偏导数）。经过推导，梯度公式非常简洁：

  • 对权重 wj​的梯度：∂wj​∂J​=m1​∑i=1m​(h(xi​)−yi​)xij​

  • 对偏置 b的梯度：∂b∂J​=m1​∑i=1m​(h(xi​)−yi​)

    可以发现，梯度实际上是所有样本的​​预测误差​​ (h(xi​)−yi​)与其对应特征 xij​的乘积的均值。

• ​​参数更新​​：

  在得到梯度后，参数沿着梯度的反方向（即损失下降最快的方向）进行更新：

  • wj​:=wj​−α∂wj​∂J​

  • b:=b−α∂b∂J​

    其中，​​α​​ 是​​学习率​​，一个重要的超参数，它控制了每一步更新的幅度。

5.逻辑回归的核心工作流程​​

逻辑回归模型的构建与训练可以概括为以下四个核心步骤：

1. ​​模型假设​​：首先，将输入特征的线性组合 wTx+b作为决策基础。然后，通过 ​​Sigmoid 函数​​ 将这个线性得分映射到 (0, 1) 区间，得到一个直观的概率输出。

2. ​​损失函数​​：构建一个合适的损失函数来衡量模型预测概率与真实标签之间的差距。逻辑回归采用​​对数损失函数​​（或交叉熵损失），它为错误的预测赋予了较大的惩罚。

3. ​​梯度计算​​：采用梯度下降法进行优化，核心是计算损失函数关于每个模型参数（权重 w和偏置 b）的​​偏导数​​，以确定损失函数下降最快的方向。

4. ​​参数更新​​：根据计算得到的梯度，沿着梯度反方向​​迭代更新​​参数 w和 b，逐步降低损失，直至模型收敛。

6.一个通俗的理解​​

我们可以用一个更形象的方式来理解逻辑回归：

• ​​线性部分（定位）​​：公式 z=wTx+b就像一个评分系统。它根据特征的权重（重要性）为数据点计算一个“分数”。这个分数决定了该数据点在特征空间中的“位置”，正分倾向于一类，负分倾向于另一类。

• ​​非线性映射（压缩与转换）​​：​​Sigmoid 函数​​ 的作用类似于一个“概率压缩器”。它将范围无限的线性得分 z挤压并平滑地转换到 0 到 1 之间，从而得到一个有明确意义的概率值。

• ​​概率决策（判定）​​：最终，我们将得到的概率值与一个预设的​​阈值​​（默认为 0.5）进行比较，从而完成最终的分类决策。这相当于设定了一条“置信线”，概率高于此线则归为一类，低于则归为另一类。

7.优缺点与典型应用场景​​

​​优点​​

• ​​模型简单高效​​：原理直观，实现和训练的计算成本较低，非常适合​​中小规模数据集​​。

• ​​提供概率输出​​：不同于直接输出类别的模型，它能输出属于某一类的​​概率​​，为风险控制等需要概率评估的场景提供了更大灵活性。

• ​​可解释性强​​：模型的​​权重系数​​有明确的含义，其绝对值大小和正负直接反映了对应特征对预测结果的​​影响程度和方向​​。

• ​​易于扩展​​：可通过引入 ​​L1 或 L2 正则化​​ 来防止模型过拟合，提升泛化能力。

​​缺点​​

• ​​线性限制​​：其本质是一个广义线性模型，​​无法自动捕捉特征间复杂的非线性关系​​，对于非线性可分的数据集效果不佳。

• ​​对异常值敏感​​：输入数据中的​​异常值​​会显著影响线性决策边界的位置，从而对模型性能造成较大干扰。

• ​​依赖特征工程​​：为了达到最佳性能，通常需要仔细地进行​​特征工程​​（如特征变换、组合等）来弥补其线性假设的不足。

• ​​原生二分类​​：标准逻辑回归​​天然用于二分类问题​​，处理多分类问题需要借助“一对多”等策略进行扩展。

​​适用场景​​

• 需要解决​​二分类​​问题。

• 特征与目标标签之间大致存在​​线性或近似线性​​的关系。

• 任务要求模型不仅给出分类结果，还需要提供​​分类的置信度​​（概率）。

• 数据量不大，且对模型的​​可解释性​​有一定要求。

完整案例：客户流失预测

1. 数据模拟
使用make_classification生成1000个样本，包含“客户满意度”和“月消费金额”两个特征。

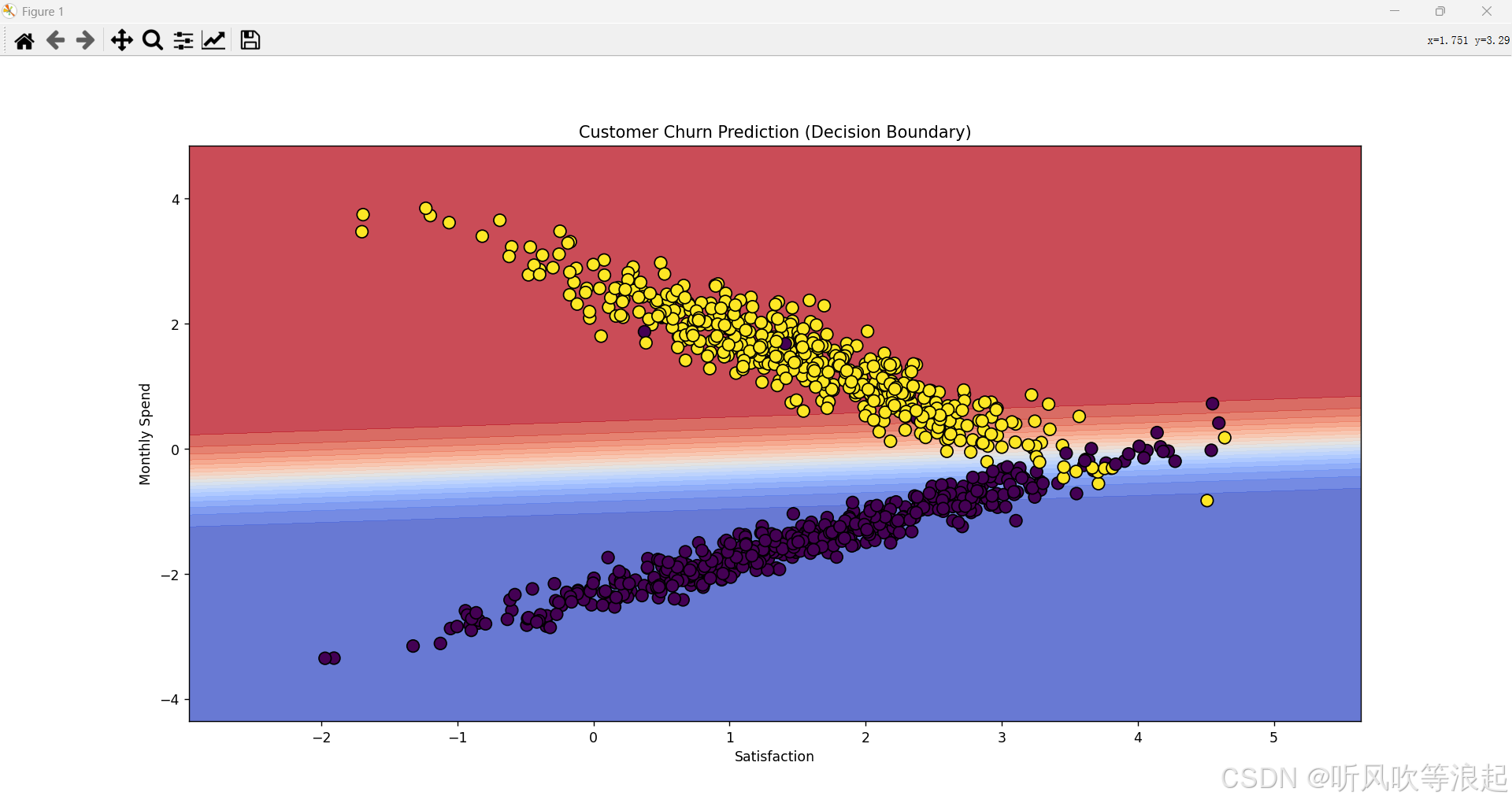
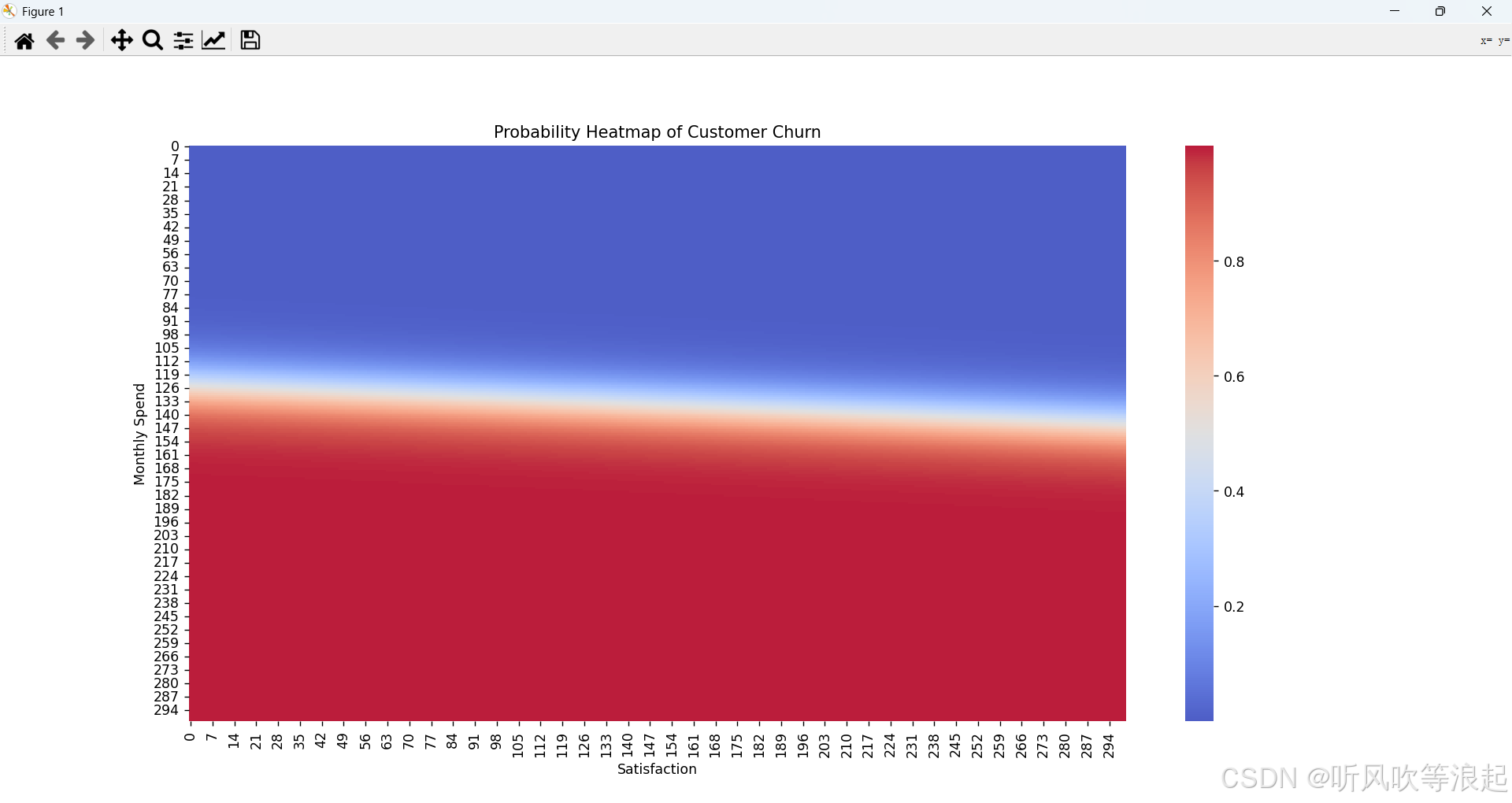
2. 建模与可视化

• 使用LogisticRegression训练模型

• 绘制决策边界图：展示分类区域

• 绘制概率热力图：显示流失概率分布

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification# 1. 数据模拟
np.random.seed(42)
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2,n_redundant=0, n_clusters_per_class=1,class_sep=1.5, random_state=42)
X = pd.DataFrame(X, columns=["Satisfaction", "Monthly_Spend"])
y = pd.Series(y, name="Churn")# 2. 训练模型
model = LogisticRegression()
model.fit(X, y)# 3. 绘制决策边界
def plot_decision_boundary(X, y, model, ax):x_min, x_max = X.iloc[:, 0].min() - 1, X.iloc[:, 0].max() + 1y_min, y_max = X.iloc[:, 1].min() - 1, X.iloc[:, 1].max() + 1xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),np.linspace(y_min, y_max, 300))Z = model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]Z = Z.reshape(xx.shape)ax.contourf(xx, yy, Z, alpha=0.8, cmap="coolwarm", levels=np.linspace(0, 1, 20))ax.scatter(X.iloc[:, 0], X.iloc[:, 1], c=y, edgecolors='k', cmap="viridis", s=80)ax.set_xlabel("Satisfaction")ax.set_ylabel("Monthly Spend")ax.set_title("Customer Churn Prediction (Decision Boundary)")# 4. 绘制概率热力图
def plot_probability_heatmap(X, model):plt.figure(figsize=(10, 8))x_min, x_max = X.iloc[:, 0].min() - 1, X.iloc[:, 0].max() + 1y_min, y_max = X.iloc[:, 1].min() - 1, X.iloc[:, 1].max() + 1xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),np.linspace(y_min, y_max, 300))Z = model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1].reshape(xx.shape)sns.heatmap(Z, cmap="coolwarm", alpha=0.9)plt.title("Probability Heatmap of Customer Churn")plt.xlabel("Satisfaction")plt.ylabel("Monthly Spend")plt.show()# 5. 绘图展示
fig, ax = plt.subplots(figsize=(12, 8))
plot_decision_boundary(X, y, model, ax)
plt.show()plot_probability_heatmap(X, model)