机器学习高级-Chapter 04-概率论与贝叶斯分类

1 概率论

以下6个方面对概率论进行讲解
1.均匀分布
2.正态分布
3.数学期望
4.方差
5.标准差
6.多维随机变量及其分布

1.1 均匀分布

连续概率分布中最简单的均匀分布

假设某站的公交车每10min来一趟，那么乘客候车时间X是(0,10),这个X就是服从均匀分布的随机变量。

均匀分布的高度是一致的也就每一份概率是相同的。

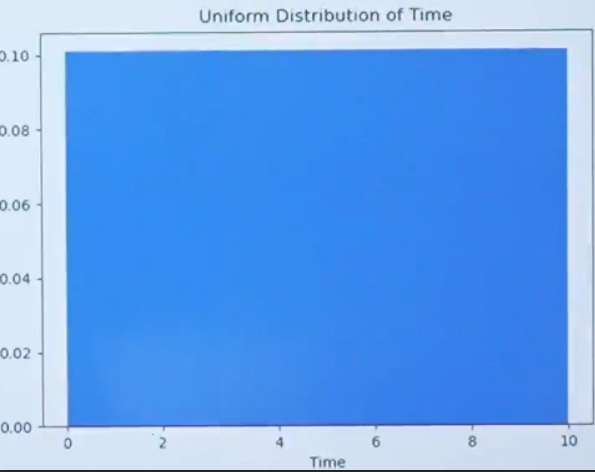
均匀分布的概率密度函数形式为：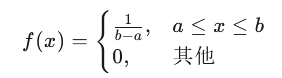

1.2 正态分布

正态分布（Normal distribution），又称高斯分布（Gaussian distribution），是统计学中最重要、最常见的连续型概率分布之一。

一、概率密度函数（PDF）

若随机变量 X 服从参数为 μ 和 σ2 的正态分布，记作：X∼N(μ,σ2)

则其概率密度函数为：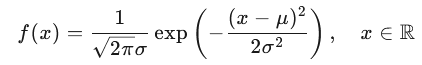

其中：

• μ：均值（mean），决定分布的中心位置

• σ：标准差（standard deviation），决定分布的“胖瘦”程度，σ>0

二、标准正态分布

当 μ=0、σ=1 时，称为标准正态分布：Z∼N(0,1)

其概率密度函数为：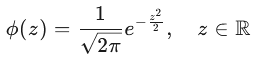

正态分布的引入

案例：在投硬币时，当投掷3次，“字”出现的次数会得到一个图像，如下所示：

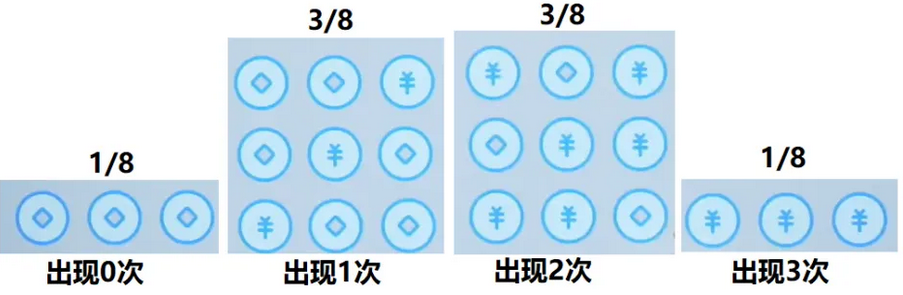
假设当投掷的次数变多之后，来看一下这个图示：

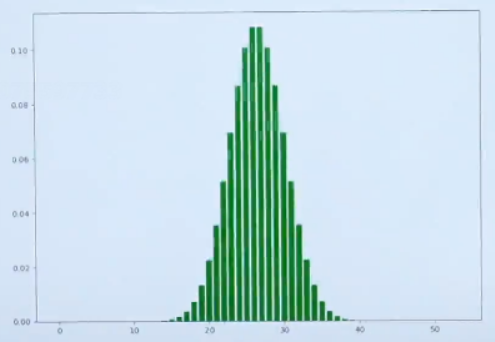
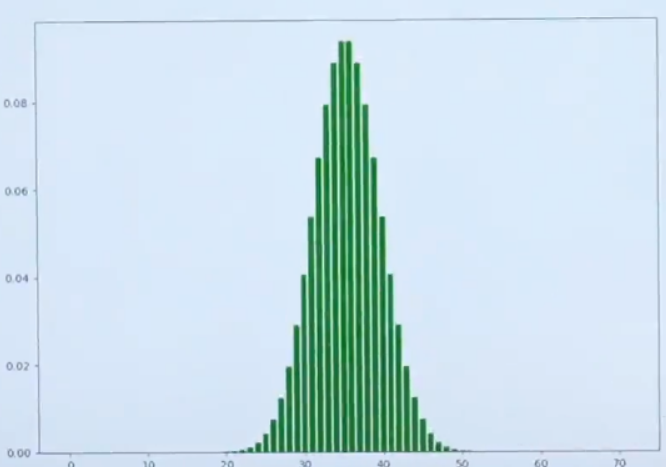
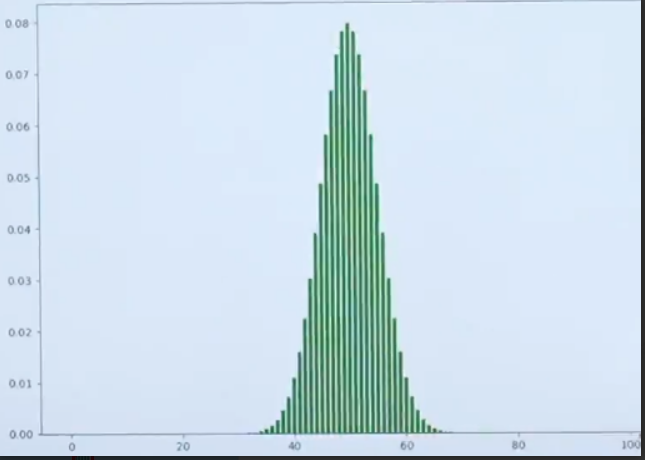
图中可以观察到，不论是投掷50次还是100次，都类似于钟形图的图像。图像离远一点看，就可以把它看作一个曲线如下图所示：

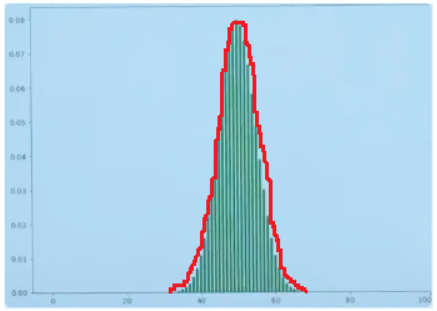
这个曲线就是正态分布。刚才举的例子，离散的二项分布，当n特别大的时候，图像是接近于正态分布。当前是从离散引入直观理解。

1.3 数学期望

数学期望其实和均值是画等号的

数学期望（Expectation / Expected Value）是概率论里对随机变量平均取值的度量，记作 E[X]。
一句话：把随机变量所有可能取值按概率加权平均，就是它的数学期望。

离散型随机变量的数学期望：

设 X 的分布列为

则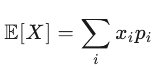

数学期望的引入：

期望是描述一个随机变量平均值的概念。对于离散型随机变量，期望E(X)的计算公式为：

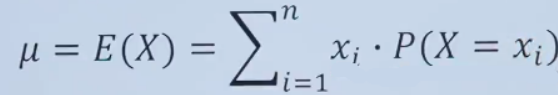
其中，

μ表示数学期望

E(X)表示随机变量X的数学期望

是随机变量X可能的取值，

表示随机变量X取值为的概率。

n表示所有可能取值的个数

案例：

考虑一个投掷一枚标准六面骰子的情况。随机变量X表示掷骰子的结果。计算骰子的期望：

1.4 方差

方差是衡量随机变量分布离散程度的指标。对于离散型随机变量，方差Var(X)的计算公式为：

  μ是随机变量的期望

例子1：

与朋友打赌投硬币，但是如果“字”面朝上，那么就赢1块钱，否则就输1块钱，数学期望是多少？

E(X)=1∗0.5+(−1)∗0.5=0

例子2：

与朋友打赌投硬币，但是如果“字”面朝上，那么就赢100块钱，否则就输100块钱，数学期望是多少？

E(X)=100∗0.5+(−100)∗0.5=0

问：如果让你去玩的话，你感觉哪个风险更大？

直观上感觉第二个风险比较大！

那怎么用数学方法去量化这个风险？

如下图所示，将1 -1 ，100 -100画成了柱状图。

它们的概率都是0.5，两个例子的柱状图的均值是一样的，都是0位置。

但是两个柱状图的差值(也就是距离)是不一样的，差值其实是衡量风险量化的一个指标，

差值越大风险越大。

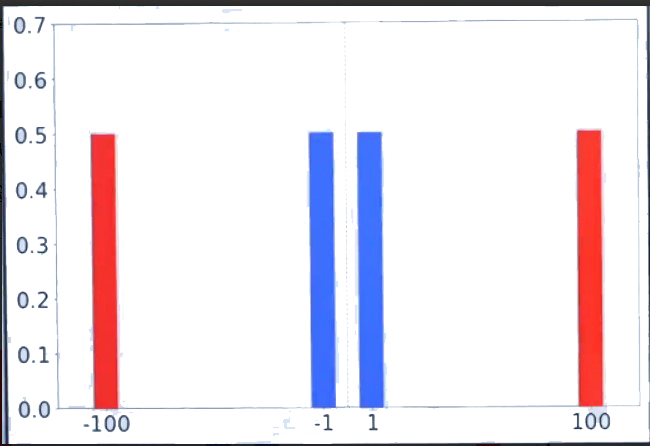
两个案例均值都是0。

为啥风险不一样但是计算出的风险感觉是一样呢，观察公式是不是都有正负号，正负抵消了。

如何消除抵消？

在线性回归里是不是已经提出方案了就是求平方。

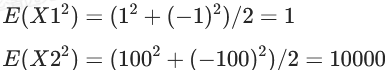
1.5 标准差

方差的特性：方差可以提供关于数据的离散程度的信息，但它的单位是数据单位的平方，这使得

它不太直观

比如，身高的单位是m(米),但是使用方差计算离散程度单位是m*m，对于身高来讲，m*m显然是不对的。

怎么得到m(米)呢，直接开方就可以了

对方差开方从而得到数据单位：

上面公式得到的就是标准差，标准差用到的比较多，因为标准差的单位和随机变量X的单位是一致的。

正态分布：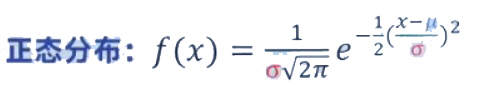

在正态分布中σ就是标准差。μ是数学期望或均值。

μ能实现它的平移 ，通过σ可以实现“陡峭”或“扁平”程度的调整

方差和标准差的作用：

方差衡量的是每个数值与总体平均值的偏离程度的平方的平均数。

标准差是方差的平方根，它以原始数据单位来衡量数据的离散程度。

1.6 多维随机变量及其分布

这里不详细讲，对于机器学习和深度学习的学习了解一下就行。

多维随机变量是指由多个随机变量组成的向量，其取值可以使多维空间中的一个点。多维随机变量的分布描述了这个向量的概率分布情况，即描述了各个随机变量之间以及它们与其他变量之间的关系。

联合分布描述了两个或多个随机变量同时取不同取值的概率情况。

多维正态分布：也称为多元正态分布，是最常见的多维分布之一。它具有与一维正态分布相似的性质，

但是描述了多个随机变量的联合分布情况。

多项分布：描述了多个类别的离散随机变量的分布，例如投掷一枚骰子多次的结果。

协方差矩阵：用于描述多维随机变量之间的相关性和方差的矩阵。

2 贝叶斯分类

2.1 贝叶斯原理

贝叶斯算法是基于贝叶斯公式的，其公式为：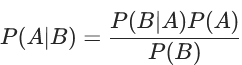

其中 P(A) 叫做先验概率，P(B|A) 叫做条件概率， P(B) 叫做观察概率， P(A|B) 叫做后验概率，也是我们求解的结果，通过比较后验概率的大小，将后验概率最大的类别作为真实类别。

1. 先验概率（Prior Probability）

先验概率是指在观察到任何数据或证据之前，我们对某件事情发生的初始信念或概率估计。它是根据以往的经验、知识或者假设来确定的。先验概率反映了我们对未知参数或假设的先验知识。

2.似然概率是什么？=P(B|A) 条件概率

似然概率（likelihood）是一个统计学概念，通常用于描述给定模型参数的情况下观测数据出现的可能性。似然是概率论中的一个重要概念，但它与概率有所不同。似然通常用来衡量某个假设（比如参数取值）与实际观测数据之间的一致性程度。