Java 数学类详解：Math 类常用方法（abs/sqrt/random 等）一篇掌握

        在 Java 开发中，无论是计算绝对值、开平方，还是生成随机数，我们都离不开java.lang.Math类。这个类就像一个 "数学工具箱"，封装了大量常用的数学运算方法，且所有方法都是静态的，直接通过Math.方法名()即可调用。今天我们就深入剖析 Math 类的核心方法、使用场景、底层原理和避坑指南，配上直观图解，让你一次吃透！

一、Math 类的 "身世"：你需要知道的基础

在学习具体方法前，先了解 Math 类的 3 个关键特性：

• 所在包：java.lang（无需 import，直接使用）；
• 实例化：构造方法被private修饰，不能创建对象（所有方法都是静态的）；
• 底层实现：大部分方法是native的（调用底层 C/C++ 代码实现），执行效率极高。

Math 类还定义了两个常用数学常量：

Math.PI;  // 圆周率 π（约3.141592653589793）
Math.E;   // 自然常数 e（约2.718281828459045）

二、核心方法分类详解

1. 绝对值与符号操作：abs ()、signum ()

（1）abs()：求绝对值

支持int、long、float、double四种类型，返回非负值。

Math.abs(-5);      // 5（int）
Math.abs(-3.14);   // 3.14（double）
Math.abs(-9L);     // 9L（long）

场景：需要忽略数值符号时（如计算距离、差值）。例如：

// 计算两点x坐标的距离（忽略方向）
int x1 = 3, x2 = 7;
int distance = Math.abs(x1 - x2);  // 4

（2）signum()：获取数值符号（Java 1.5+）

返回数值的符号：正数返回1.0，负数返回-1.0，0 返回0.0（仅支持float和double）。

Math.signum(5.2);   // 1.0
Math.signum(-3.8);  // -1.0
Math.signum(0.0);   // 0.0

场景：判断数值正负方向，例如游戏中角色移动方向判断。

2. 算术运算：pow ()、sqrt ()、cbrt ()、hypot ()

（1）pow(a, b)：计算 a 的 b 次方

返回a^b（注意：a 为负数时，b 必须为整数，否则返回 NaN）。

Math.pow(2, 3);    // 8.0（2^3）
Math.pow(10, -2);  // 0.01（10的-2次方）
Math.pow(-2, 3);   // -8.0（合法，b是整数）
Math.pow(-2, 0.5); // NaN（非法，负数不能开平方）

（2）sqrt(a)：开平方，cbrt(a)：开立方

• sqrt(a)：返回 a 的平方根（a 必须≥0，否则返回 NaN）；
• cbrt(a)：返回 a 的立方根（支持负数）。

Math.sqrt(16);    // 4.0
Math.sqrt(-4);    // NaN（错误）
Math.cbrt(-8);    // -2.0（正确，立方根支持负数）

场景：几何计算（如求对角线长度）。例如：

// 求边长为3、4的直角三角形斜边（勾股定理：c=√(a²+b²)）
double a = 3, b = 4;
double c = Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2));  // 5.0

（3）hypot(a, b)：求√(a² + b²)（Java 1.5+）

        专门用于计算直角三角形的斜边，等价于sqrt(a² + b²)，但能避免a² + b²溢出（底层做了优化）。

Math.hypot(3, 4);  // 5.0（等价于上面的例子，但更安全）

3. 取整操作：ceil ()、floor ()、round ()、rint ()

这四个方法用于将浮点型转换为整数，但规则不同，是高频考点！

方法	规则	例子（输入→输出）
ceil(a)	向上取整（取大于等于 a 的最小整数）	3.2→4.0；-1.5→-1.0
floor(a)	向下取整（取小于等于 a 的最大整数）	3.8→3.0；-1.2→-2.0
round(a)	四舍五入（double 返回 long，float 返回 int）	3.4→3；3.5→4；-3.5→-3
rint(a)	取最接近的整数（若距离相等，取偶数）	3.5→4.0；2.5→2.0

Math.ceil(2.1);    // 3.0
Math.floor(2.9);   // 2.0
Math.round(2.5f);  // 3（int）
Math.rint(3.5);    // 4.0（double）

场景：数值格式化（如保留整数位）、分页计算（向上取整求总页数）。例如：

// 计算总页数（10条/页，32条数据需4页）
int total = 32, pageSize = 10;
int totalPages = (int) Math.ceil(total * 1.0 / pageSize);  // 4

4. 三角函数：sin ()、cos ()、tan ()、toRadians ()

Math 类的三角函数基于弧度计算，而非角度。若输入角度，需先用toRadians()转换为弧度（180°=π 弧度）。

// 计算30°的正弦值（sin30°=0.5）
double degrees = 30;
double radians = Math.toRadians(degrees);  // 转换为弧度
Math.sin(radians);  // 约0.49999999999999994（接近0.5，浮点精度问题）

注意：浮点运算存在精度误差，如需精确比较，需指定误差范围（如|a - b| < 1e-6）。

5. 随机数生成：random ()

Math.random()返回一个[0.0, 1.0)区间的随机 double 值（包含 0.0，不包含 1.0）。

（1）生成指定范围的随机数

通过公式扩展范围：

• 生成[min, max)的随机整数：(int)(Math.random() * (max - min) + min)
• 生成[min, max]的随机整数：(int)(Math.random() * (max - min + 1) + min)

// 生成[1, 100]的随机整数（如抽奖号码）
int randomNum = (int)(Math.random() * 100 + 1);

（2）底层原理与线程安全

Math.random()底层依赖java.util.Random的静态实例，源码如下：

public static double random() {return RandomNumberGeneratorHolder.randomNumberGenerator.nextDouble();
}private static final class RandomNumberGeneratorHolder {static final Random randomNumberGenerator = new Random();
}

• 线程安全：Random的nextDouble()是线程安全的（用了 CAS 锁），但多线程并发时可能因竞争导致性能下降；
• 替代方案：Java 7 + 的ThreadLocalRandom（线程私有，无竞争，性能更好）。

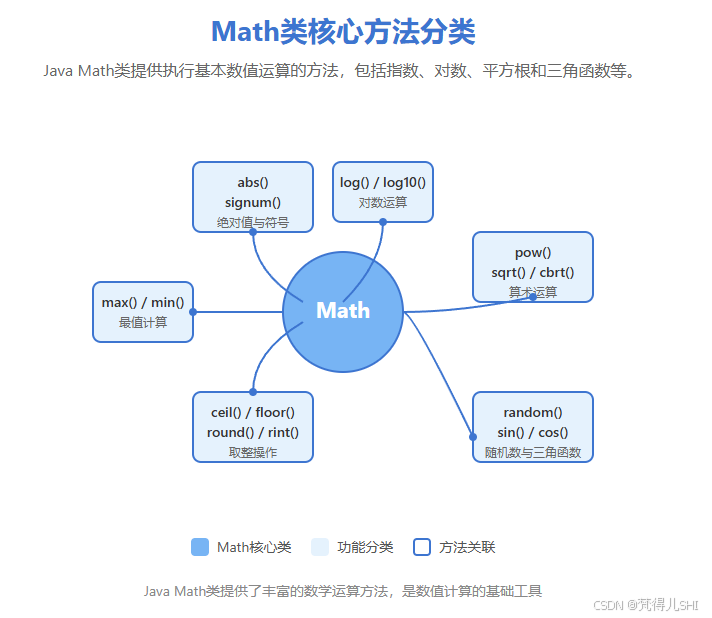
Math 类核心方法图解

三、避坑指南：这些 "坑" 你必须知道

1. 浮点精度问题

float和double的运算存在精度误差，例如：

Math.sqrt(2);  // 1.4142135623730951（实际√2是无理数，只能近似）
Math.sin(Math.PI);  // 1.2246467991473532E-16（接近0，但非0）

解决：如需精确比较，用BigDecimal，或判断两数差值是否小于极小值（如1e-6）。

2. random()的范围误解

Math.random()返回[0.0, 1.0)，不包含 1.0，因此生成[0, n]的整数时需注意：

// 错误：可能生成n+1（因为1.0 * n可能等于n，但random()不返回1.0，所以实际安全）
// 正确：生成[0, 5]的整数
int num = (int)(Math.random() * 6);  // 0-5（正确，6种可能）

3. 整数溢出风险

pow()返回double，若用它计算大整数次方，可能因转换为int导致溢出：

// 错误：2^30是1073741824，2^31是2147483648，超过int最大值（2^31-1）
int result = (int) Math.pow(2, 31);  // 结果为-2147483648（溢出）

解决：大整数运算用BigInteger。

四、总结

Math 类是 Java 处理数学运算的 "利器"，核心价值在于：

• 便捷性：封装常用运算，无需重复实现（如取整、开方）；
• 高效性：native 方法调用底层代码，性能优于手动实现；
• 安全性：优化了溢出、精度等问题（如hypot()避免平方和溢出）。

        掌握abs()、sqrt()、round()、random()等核心方法，理解浮点精度和范围规则，能让你在数值计算场景中事半功倍。记住：遇到数学运算先查 Math 类，避免重复造轮子！

最后，建议大家动手测试每个方法的边界情况（如输入 0、负数、极值），加深对方法行为的理解。

---

版权声明：本博客内容为原创，转载请保留原文链接及作者信息。