牛客算法_动态规划

动态规划

问题的特点：f(n) 依赖f(n-1) 

1、 斐波那契数列

递归实现

2、青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

思路：递归实现

3、最小花费爬楼梯

给定一个整数数组 cost cost  ，其中 cost[i] cost[i]  是从楼梯第i i 个台阶向上爬需要支付的费用，下标从0开始。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

数据范围：数组长度满足 1≤n≤105 1≤n≤105  ，数组中的值满足 1≤costi≤104 1≤costi​≤104 

思路：

        爬到下标是i的楼梯的花费=min(爬到i-1楼梯的花费 + cost[i],  爬到i-2楼梯的花费 + cost[i] ), 用两个变量记录 爬到i-1楼梯的花费 和 爬到i-2楼梯的花费。

 public int minCostClimbingStairs(int[] cost) {if (cost == null || cost.length <= 0) {return -1;}if(cost.length == 1) return cost[0]; // 1个台阶if(cost.length==2) return cost[1];// 2个台阶// 初始化两个变量， dp1 = 下标为0的台阶，需要花费， dp2 = 下标为1的台阶，需要花费int dp1 = cost[0], dp2 = cost[1];// 遍历cost数组，从下标2开始for (int i = 2; i < cost.length; i++) {int temp = dp2;// 计算到达下标=i的台阶的花费// 花费为 (当前i层台阶的花费 + dp1花费， 与  当前i层台阶的花费 + dp2花费 取最小花费值)dp2 = Math.min(cost[i] + dp1, cost[i] + dp2);// 然后dp1的花费后移，改为之前的dp2dp1 = temp;}// 循环结束时，对比dp1 和 dp2的花费 取最小值return dp1 > dp2 ? dp2 : dp1;}

3、 两个字符串的最长公共子序列

思路：

4、矩阵中最小路径

一个机器人在m×n大小的地图的左上角（起点）。

机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。

可以有多少种不同的路径从起点走到终点？

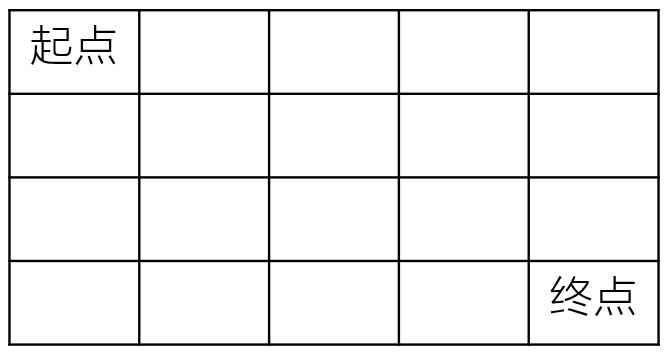
public int uniquePaths (int m, int n) {if(m == 1 || n == 1){return 1;}return uniquePaths(m, n-1) + uniquePaths(m-1, n);}

5、矩阵中最小路径和（重要）

思路：

1. 使用int[][] matrixSum记录每个小格的最小路径值

2. 先设置左边和上边的matrixSum的值

3. 从左上到右下设置每个小格的值

4. 返回右下角的值

public int minPathSum(int[][] matrix) {if (matrix == null) {return -1;}int m = matrix.length;int n = matrix[0].length;int[][] matrixSum = new int[m][n];for (int i = 0; i < m; i++) {if(i == 0){matrixSum[0][0] = matrix[0][0];}else{matrixSum[i][0] = matrixSum[i-1][0] + matrix[i][0];}}for (int j = 1; j < n; j++) {matrixSum[0][j] = matrixSum[0][j-1] + matrix[0][j];}for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){int x1 = matrixSum[i][j-1] + matrix[i][j];int x2 = matrixSum[i-1][j] + matrix[i][j];int min = x1 > x2 ? x2:x1;matrixSum[i][j] = min;}}return matrixSum[m-1][n-1];}

6、兑换零钱

给定数组arr，arr中所有的值 都为正整数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个aim，代表要找的钱数，求组成aim的最少货币数（这里说的是货币种类数，而不是总张数）。

如果无解，请返回-1.

数据范围：数组大小满足 0≤n≤100000≤n≤10000 ， 数组中每个数字都满足 0<val≤100000<val≤10000，0≤aim≤50000≤aim≤5000

要求：时间复杂度 O(n×aim)O(n×aim) ，空间复杂度 O(aim)O(aim)。

思路：

1. 用int[] dp 保存满足aim的最小货币数，初始化为aim+1(最大值，比如aim=10, 不可能由11种货币组成aim)， dp[0] = 0.

2. 从aim=1~n , 利用dp[i-1]计算dp[i]的值

3. arr[j] = y,  xx = aim - y, dp[aim - y] 如果有有效值， 则dp[aim - y] + 1（arr[j] = y 是一种货币）是一个选择。

public int minMoney(int[] arr, int aim) {//dp[i] 换得金额i能用的最少硬币数int[] dp = new int[aim + 1];//后面要比较最小值 所以每个dp的初始值都是aim+1 ， 考虑硬币额度全为1用aim枚能换aim额度 aim+1必然是越界值了Arrays.fill(dp, aim + 1);dp[0] = 0; //因为要给dp[1-1]做铺垫 所以dp[0]必须是0for (int i = 1; i < aim + 1; i++) {for (int j = 0; j < arr.length; j++) {//别越界 && 至少能换出来才换 && 能换的话 看看我用这枚硬币好 还是不用好// && 如果能用硬币你不用的话（或者压根换不出来） 那代价可是MAX值 逼着你尽可能换// i表示总金额，i = arr[j] + xxx,// dp[i - arr[j]] + 1 ：默认arr[j] 用1张// dp[i] 默认值if (i - arr[j] >= 0)dp[i] = Math.min(dp[i], dp[i - arr[j]] + 1);}}//要是流程走下来 dp值是非法值 说明换不出来return dp[aim] == aim + 1 ? -1 : dp[aim];}

6、最长上升子序列(重要)

给定一个长度为 n 的数组 arr，求它的最长严格上升子序列的长度。

所谓子序列，指一个数组删掉一些数（也可以不删）之后，形成的新数组。例如 [1,5,3,7,3] 数组，其子序列有：[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。

我们定义一个序列是 严格上升 的，当且仅当该序列不存在两个下标 ii 和 jj 满足 i<ji<j 且 arri≥arrjarri​≥arrj​。

数据范围： 0≤n≤10000≤n≤1000

要求：时间复杂度 O(n2)O(n2)， 空间复杂度 O(n)O(n)

思路：

1. dp[i]表示以arr[i]结尾时 的最长递增子序列长度

2. 数组长度从1~n逐个判断

3. 长度=i时，逐个从 i-1~0 (j)判断arr, 判断arr[j]与arr[i]大小， 计算dp[j] + 1, 取max(dp[i], dp[j]+1)

public int LIS(int[] arr) {int n = arr.length;if (n == 0) return 0;int[] dp = new int[n];     // dp[i]表示以arr[i]结尾时 的最长递增子序列长度Arrays.fill(dp, 1);int maxLen = 1;for (int i = 1; i < n; i++) {for (int j = i - 1; j >= 0; j--) {if (arr[j] < arr[i]) {// arr[j] < arr[i]，可以把arr[i]接在arr[j]后面，构成长度为dp[j]+1的递增子序列dp[i] = Math.max(dp[i], dp[j] + 1);     // 选择能构成更长递增子序列的arr[j]}}maxLen = Math.max(maxLen, dp[i]);}return maxLen;}

7、连续子数组的最大和

思路1：和第6题思路一样

1. dp[i]表示以arr[i]结尾时 的连续子数组的最大和

2. 数组长度从1~n逐个判断

3. 长度=i时，判断dp[i-1]+arr[i]与arr[i]大小， 取最大的座位dp[i],  同时算出最大的dp[i]

public int FindGreatestSumOfSubArray (int[] arr) {int n = arr.length;if (n == 0) return 0;int[] dp = new int[n];// dp[i]表示以arr[i]结尾时 的连续子数组的最大和dp[0] = arr[0];int maxSum = dp[0];for (int i = 1; i < n; i++) {dp[i] = Math.max(arr[i], dp[i-1] + arr[i]);maxSum = Math.max(maxSum, dp[i]);}return maxSum;}

思路2：暴力破解法

缺点：超时

 public int FindGreatestSumOfSubArray (int[] array) {int n = array.length;if (n == 0) return 0;if(n == 1) return array[0];int[] dp = new int[n];     // dp[i]表示以下标i开头的 连续子数组的最大和Arrays.fill(dp, Integer.MIN_VALUE);int max = Integer.MIN_VALUE;for(int i = 0; i < array.length; i++){int x = 0;for(int j = i; j < array.length; j++){x = x+array[j];dp[i] = Math.max(x, dp[i]);}max = Math.max(dp[i], max);}return max;}

8、最长回文子串

思路：

1. 设定left和right，left从0开始，right从left+ans（maxLongest） 开始，ans初始化为对整个字符串进行遍历

2. 首先是 定住left 然后找 right处和left处字符相同，然后判断 这里是不是一个回文

3. 如果是，可以直接将当前回文长度替换成最大值，因为每一次的right的起始位置一定是从left加上最大长度ans之后的位置开始

 public int getLongestPalindrome(String A) {int n = A.length();if (n == 0) return 0;if (n == 1) return 1;int maxLongest = 1;for (int left = 0; left + maxLongest < n; left++) {for (int right = left + maxLongest; right < n; right++) {if (A.charAt(left) == A.charAt(right)) {if (isReverse(left, right, A)) {maxLongest = right - left + 1;}}}}return maxLongest;}private boolean isReverse(int left, int right, String a) {while (left < right){char l = a.charAt(left);char r = a.charAt(right);if(l != r){return false;}left++;right--;}return true;}

9、打家窃舍

你是一个经验丰富的小偷，准备偷沿街的一排房间，每个房间都存有一定的现金，为了防止被发现，你不能偷相邻的两家，即，如果偷了第一家，就不能再偷第二家；如果偷了第二家，那么就不能偷第一家和第三家。

给定一个整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。

数据范围：数组长度满足 1≤n≤2×105 1≤n≤2×105  ，数组中每个值满足 1≤num[i]≤5000 1≤num[i]≤5000 

误区一：认为偷尽可能多家，才能获取最大金额。 所以计算偷奇数家和偷偶数家，两者做比较，取最大值。 这种想法是错误的， 因为小偷可以选择连续两家不偷，去偷金额最大的那家。

（当然如果是考试的话，实在想不出正确的解题方案，这个思路也能跑通一部分测试用例，也是可以提交的......）

正确思路：经典动态规划做法，用dp[length][2]数组来表示状态。dp[i][0]、dp[i][1] 分别表示不偷与偷第 i 间时，到当前房间为止的最大偷窃金额。

public int rob(int[] nums) {// int[i][j] 表示到nums[i]个门店时，j=0不偷这个门店的收益，j=1偷这个门店的收益 int[][] dp = new int[nums.length][2];dp[0][0] = 0;dp[0][1] = nums[0];for(int i = 1; i < nums.length; i++){dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]); // 取上一个门店偷与不偷的最大收益dp[i][1] = dp[i-1][0] + nums[i]; // 取上一个门店偷的收益+当前门店收益}return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);}

10、打家劫舍2

相对于第9题， 一排房间组成环形，即第1个房间和最后一个房间是相邻的。

思路：

分为第一间偷与不偷两种情况，两种情况分别按照无环的流程 求得最大偷窃金额，然后选择金额更大的那个方案。

  public int rob(int[] nums) {int n = nums.length;if (n == 1) return nums[0];// 偷第一间int tempMax = 0;int[][] dp1 = new int[n][2];dp1[0][1] = nums[0]; // 第1间dp1[1][0] = nums[0]; // 第2间不偷dp1[1][1] = nums[0]; // 第2间不能偷//注意是i<n-1 而不是i<n, 因为最后一个门店不能偷for (int i = 2; i < n - 1; i++) {dp1[i][0] = Math.max(dp1[i - 1][0], dp1[i - 1][1]);     // 这一家不偷dp1[i][1] = dp1[i - 1][0] + nums[i];                    // 这一家偷}// 因为偷了第1间，最后1间不能偷dp1[n - 1][0] = Math.max(dp1[n - 2][0], dp1[n - 2][1]);dp1[n - 1][1] = Math.max(dp1[n - 2][0], dp1[n - 2][1]);tempMax =  dp1[n - 1][0];// 不偷第一间int[][] dp2 = new int[n][2];for (int i = 1; i < n; i++) {dp2[i][0] = Math.max(dp2[i - 1][0], dp2[i - 1][1]);dp2[i][1] = dp2[i - 1][0] + nums[i];}return Math.max(tempMax, Math.max(dp2[n - 1][0], dp2[n - 1][1]));}

11、买卖股票最好时机（买入卖出1次）

假设你有一个数组prices，长度为n，其中prices[i]是股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

1.你可以买入一次股票和卖出一次股票，并非每天都可以买入或卖出一次，总共只能买入和卖出一次，且买入必须在卖出的前面的某一天

2.如果不能获取到任何利润，请返回0

3.假设买入卖出均无手续费

数据范围： 0≤n≤105,0≤val≤1040≤n≤105,0≤val≤104

要求：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n)

  public int maxProfit (int[] prices) {int n = prices.length;if(n <= 1){return 0;}int maxP = 0;int[] dp = new int[n]; // dp[i]表示第i天买入的最大收益for(int i = 0; i < n - 1; i++){int m = prices[i];int maxBig = m;for(int j = i+1; j < n; j++){if(prices[j] > m ){maxBig = Math.max(maxBig, prices[j]);}}dp[i] = maxBig - m;maxP = Math.max(maxP, dp[i]);}return maxP;}

12、买卖股票最好时机（买入卖出多次）

思路1：投机取巧法

        只要涨我就卖，当天我可以卖了再买。  其实是看到了第二天会涨才决定第一天买入，这和实际情况完全不一致。

        A < B < C,  那么C-A = (B-A)+(C-B),  所以可以分区间计算大小 然后相加。

 public int maxProfit2 (int[] prices) {int profile = 0;for(int i = 1; i < prices.length; i++){if(prices[i] > prices[i-1]){profile += prices[i]-prices[i-1];}}return profile;}

思路2：同第9题打家劫舍的思路

1.定义 int[][] dp ， dp[i][0] 表示第 i 天不持有股票最大收益；dp[i][1]表示第 i 天持有股票最大收益。注意dp[0]和dp[1]的配置

2. 从下标1~n-1遍历，计算每天位置对应的最大收益

3. 计算出最大收益

public int maxProfit22(int[] prices) {int n = prices.length;if (n <= 1) {return 0;}// int[i][0]:第i天未持股的最大收益， int[i][1]:第i天持股的最大收益int[][] dp = new int[n + 1][2];dp[0][0] = 0;dp[0][1] = Integer.MIN_VALUE; // 第0天持有股票，这种情况不存在dp[1][0] = 0;dp[1][1] = prices[0] * -1;int profile = 0;for (int index = 1; index < prices.length; index++) {int i = index + 1; // 第i天dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[index]); // 今天未持股：前一天未持股  or 前一天持股但是今天卖出了dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[index]); // 今天持股：前一天持股  or 前一天未持股但是今天买入了profile = Math.max(dp[i][0], dp[i][1]);}return profile > 0? profile : 0;}