当前位置：首页 > news >正文

对于消失的数字以及右旋字符数组的题目解析

news 2025/10/10 16:41:28

开篇介绍：

Hello 大家！我们又见面啦～在上一篇博客中，我们系统梳理了时间复杂度与空间复杂度的核心概念 —— 从大 O 表示法的定义，到不同复杂度（如 O (1)、O (logn)、O (n)、O (n²)）的量级差异，再到空间复杂度中 “额外空间” 与 “输入输出空间” 的区分。但仅仅掌握理论框架，远不足以应对实际算法问题中的复杂度分析与优化需求。

因此，在本篇博客中，我将通过两道经典例题，带大家从 “概念理解” 走向 “实战应用”—— 不仅会拆解每道题的多种解法，对比不同解法的复杂度差异，还会延伸出算法设计中 “降维优化”“空间换时间” 等核心思路。尤其值得一提的是，其中一道题的某一种解法，我们在上篇博客的复杂度分析案例中曾简要提及，而今天我会在此基础上补充另外两种更优解法，帮大家构建 “一题多解、多解比优” 的思维习惯。

老规矩，在正式讲解前，先为大家附上两道题的官方题目链接，方便大家提前思考或对照原题细节：面试题 17.04. 消失的数字 - 力扣（LeetCode）https://leetcode.cn/problems/missing-number-lcci/submissions/663203686/

189. 轮转数组 - 力扣（LeetCode）https://leetcode.cn/problems/rotate-array/description/

下面，就让我们开始我们的解题之旅。

面试题 17.04. 消失的数字：

这道题的难度是不大的，我们先看题目：

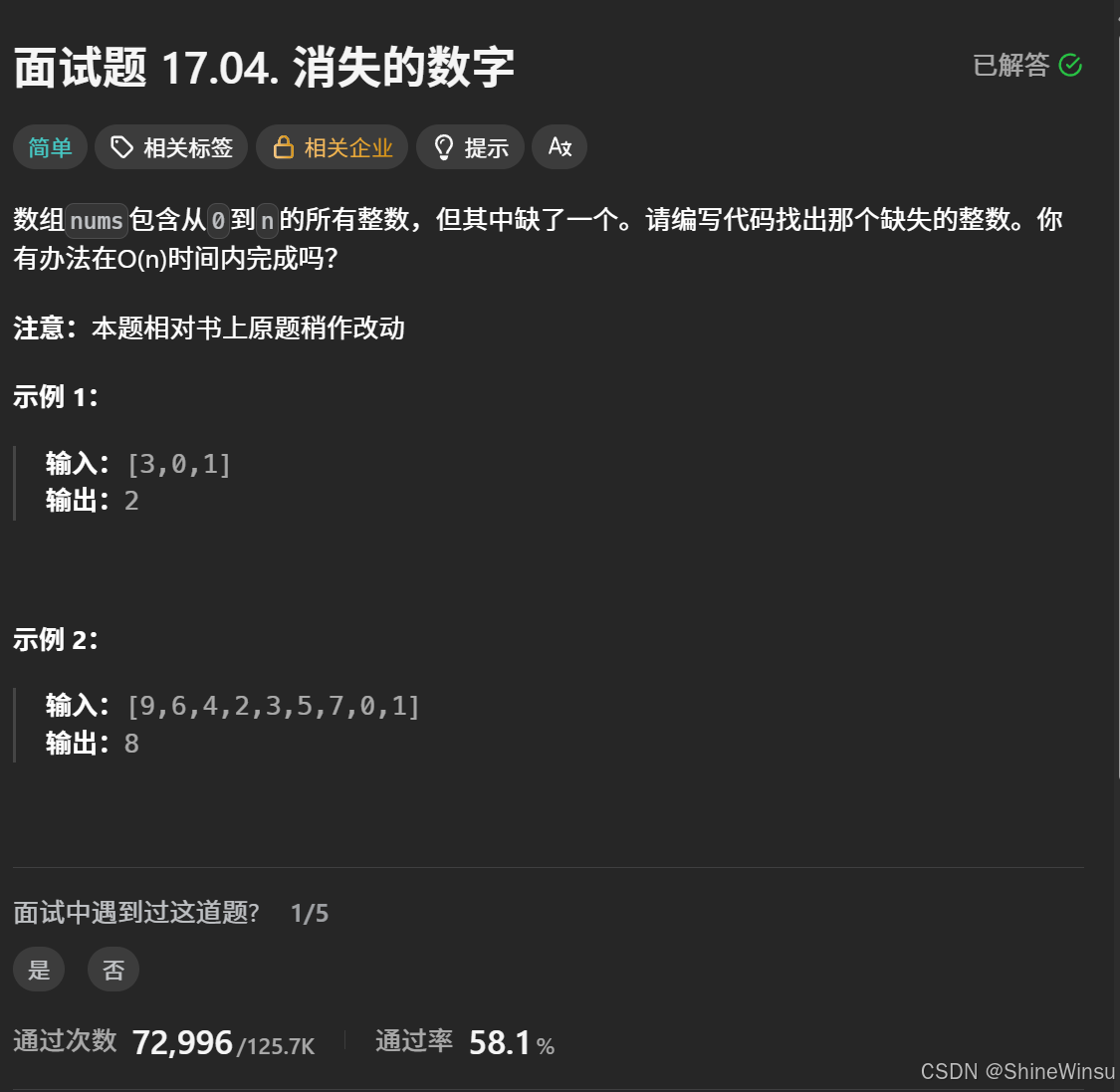
题意分析：

输入输出

输入：一个数组 nums，这个数组包含了从 0 到 n 的所有整数，但缺少其中一个。这里的 n 是一个隐含的数，它的值等于数组原本应该有的元素个数减一（因为原本应该有 n + 1 个元素，从 0 到 n）。例如，示例 1 中输入数组是 [3, 0, 1]，原本应该有 0、1、2、3 这 4 个元素（n = 3），所以缺少的是 2；示例 2 中输入数组是 [9, 6, 4, 2, 3, 5, 7, 0, 1]，原本应该有 0 到 9 这 10 个元素（n = 9），所以缺少的是 8。
输出：找出数组中缺失的那个整数。

约束条件

要求在 O(n) 的时间复杂度内完成。这意味着我们的算法只能遍历数组常数次（比如一次或两次），不能使用嵌套循环等时间复杂度为 O(n²) 及更高的方法。

那么对于这道题，我给大家提供三种方法：

方法一：

这第一个方法呢，其实就是一个思路，是不适合用来解题的，具体如下：

首先我们要把这个数组中的数据全部排序，因为题目说了给的是无序的数据，那么我们要找到消失的数字，既可以通过排序，然后看一下哪个数字的下一个数字不是这个数字加1得到的，有出现的话，那么这个数字+1就是消失的数字。

思路是挺好，但是它的时间复杂度却是不尽人意，首先我们进行排序，一般是用冒泡排序，它的时间复杂度就是O（N^2）了，更别说后续查找还要遍历数组，这远远超过了题目所要求的O（N）的时间复杂度。

所以这第一个思路也就是无法实践了，但是我们依旧可以分析这个思路，毕竟俗话说的好，多一个方法就是多一条路子。

方法二：

这个方法，就可以用于解决题目了，什么思路呢？其实它和数学有关。

题目是说从0到n丢了一个数字，那么也就是说，这个数组中，除了消失的数字之外，其余的从0到n的数字都在呢。

那么，我们就可以使用相加来进行解答，我们把0到n的所有数字全部相加起来(这里大家遍历相加亦或是使用等差数列公式求和都可以)，然后再减去数组的数据之和，最后的结果，就是消失的数字，为了方便大家理解，我给大家一些例子:

例子 1

假设 n = 4，原本应该有的数字是 0、1、2、3、4，现在数组是 [0, 1, 3, 4]。

首先计算 0 到 4 的和：根据等差数列求和公式，和为 (0 + 4) * 5 / 2 = 10。
然后计算数组中元素的和：0 + 1 + 3 + 4 = 8。
用前者减去后者：10 - 8 = 2，所以缺失的数字就是 2。

例子 2

假设 n = 5，原本数字是 0、1、2、3、4、5，数组是 [0, 2, 3, 4, 5]。

0 到 5 的和：(0 + 5) * 6 / 2 = 15。
数组元素和：0 + 2 + 3 + 4 + 5 = 14。
差值：15 - 14 = 1，缺失的数字是 1。

例子 3

假设 n = 1，原本数字是 0、1，数组是 [1]。

0 到 1 的和：(0 + 1) * 2 / 2 = 1。
数组元素和：1。
差值：1 - 1 = 0，缺失的数字是 0。

如此，我们就能在时间复杂度为O（N）的情况下解决此题，我们看代码：

int missingNumber(int* nums, int numsSize) {// 计算0到n的总和（n等于数组长度）int n = numsSize;int sum = 0;for (int i = 0; i <= n; i++) {sum += i;}// 减去数组中所有元素的值for (int i = 0; i < n; i++) {sum -= nums[i];}// 剩余的sum就是缺失的数字return sum;
}

简简单单。

方法三：

OiOi，这个方法可就牛波一了，它就是，我们的异或^，大家应该知道^的性质吧，不知道的可以去看一下我的这篇博客：

那么对于这道题，我们就可以利用^的性质去解题，那么问题来了，题目所给的数组也没有相同的数字呀，那怎么用^呢？诶大家，既然题目不给我们，那就我们自己创造呗。

我们可以用空间复杂度换时间复杂度，这个我们上一篇博客中有所提及，所以，我们可以去将0到n的所有数去与数组中的所有数据进行^，最后的结果便是消失的数字，我同样给大家一些例子帮助大家理解：

要理解用异或（`^`）解决 “消失的数字” 问题，得先回顾异或的关键性质：

任何数和0异或，结果还是它本身，即 a ^ 0 = a；
任何数和自身异或，结果为 0，即 a ^ a = 0；
异或满足交换律和结合律，即 a ^ b ^ c = a ^ c ^ b = (a ^ b) ^ c 等。

例子 1：简单场景（小范围数字）

假设 n = 3，原本完整的数字集合是 {0, 1, 2, 3}，但数组 nums = [0, 1, 3]（缺失 2）。

我们的操作是：把 0~n 的所有数，和数组里的所有数依次异或。

步骤分解：

初始化异或结果 result = 0；
先异或 0~3 的所有数：result = 0 ^ 0 ^ 1 ^ 2 ^ 3；
再异或数组 nums 里的所有数：result = (0 ^ 0 ^ 1 ^ 2 ^ 3) ^ 0 ^ 1 ^ 3；
根据异或性质化简：
- 0 ^ 0 = 0，1 ^ 1 = 0，3 ^ 3 = 0；
- 剩下 0 ^ 0 ^ 0 ^ 2 = 2；
最终 result = 2，也就是缺失的数字。

例子 2：稍复杂场景（大范围数字）

假设 n = 5，原本完整的数字集合是 {0, 1, 2, 3, 4, 5}，数组 nums = [0, 2, 3, 4, 5]（缺失 1）。

步骤分解：

初始化 result = 0；
异或 0~5 的所有数：result = 0 ^ 0 ^ 1 ^ 2 ^ 3 ^ 4 ^ 5；
异或数组 nums 里的所有数：result = (0 ^ 0 ^ 1 ^ 2 ^ 3 ^ 4 ^ 5) ^ 0 ^ 2 ^ 3 ^ 4 ^ 5；
化简：
- 0 ^ 0 = 0，2 ^ 2 = 0，3 ^ 3 = 0，4 ^ 4 = 0，5 ^ 5 = 0；
- 剩下 0 ^ 0 ^ 1 = 1；
最终 result = 1，即缺失的数字。

例子 3：边界场景（缺失开头或结尾）

缺失开头（0）：
假设 n = 2，完整集合 {0, 1, 2}，数组 nums = [1, 2]。
异或过程：(0 ^ 1 ^ 2) ^ 1 ^ 2 = 0 ^ (1 ^ 1) ^ (2 ^ 2) = 0，结果为缺失的 0。
缺失结尾（n）：
假设 n = 4，完整集合 {0, 1, 2, 3, 4}，数组 nums = [0, 1, 2, 3]。
异或过程：(0 ^ 1 ^ 2 ^ 3 ^ 4) ^ 0 ^ 1 ^ 2 ^ 3 = 4 ^ (0 ^ 0) ^ (1 ^ 1) ^ (2 ^ 2) ^ (3 ^ 3) = 4，结果为缺失的 4。

核心逻辑总结

因为除了缺失的数字，其余数字在 “0~n” 和 “数组” 中都恰好出现两次。根据异或 “相同数异或为 0，0 和任何数异或为自身” 的性质，把这些数全部异或后，重复的数会相互抵消（异或成 0），最后剩下的就是只出现一次的缺失数字。

这种方法的时间复杂度是 O(n)（只需遍历两次：一次 0~n，一次数组），空间复杂度是 O(1)（只需要一个变量存异或结果），是非常高效的解法～

由此，我们的方法三就大功告成，下面给出完整代码：

int missingNumber(int* nums, int numsSize) {int n = numsSize;int result = 0;  // 初始化为0，因为0与任何数异或结果都是该数本身// 第一步：将数组中的所有元素进行异或for (int i = 0; i < n; i++) {result ^= nums[i];//这里可以当做是//eg：sum=3^0^1}// 第二步：将0到n的所有数字与上一步结果进行异或for (int i = 0; i <= n; i++) {result ^= i;//将上面的sum代入就是：//sum=3^0^1 ^0^1^2^3==2}// 最终结果即为缺失的数字return result;
}

接下来，我们进行下一题的解析：

189. 轮转数组：

这道题大家可以看一下这一篇博客进行熟悉熟悉：

我们看题目：

题意分析：

输入输出

输入：
- 一个整数数组 nums。
- 一个非负整数 k，表示将数组元素向右轮转的位置数。
输出：经过向右轮转 k 个位置后的数组（注意是在原数组上进行修改，不是返回新数组）。

操作定义

“向右轮转 k 个位置” 的含义是：把数组的最后 k 个元素移动到数组的前面，其余元素依次后移。例如示例 1 中，数组 [1,2,3,4,5,6,7] 向右轮转 3 步，最后 3 个元素 5,6,7 移到前面，得到 [5,6,7,1,2,3,4]。

约束条件

数组长度范围：1 <= nums.length <= 10^5，说明数组规模可能较大，需要考虑算法的时间和空间复杂度。
元素取值范围：-2^31 <= nums[i] <= 2^31 - 1，涵盖了整数的大部分取值范围。
k 的范围：0 <= k <= 10^5，k 可能很大，甚至超过数组长度，这时候需要考虑对 k 进行取模运算（因为轮转数组长度的整数倍次后，数组会回到原状态）。

方法一：

这个方法一就是上文中所提到的那一篇博客所提供的解法，只不过那个方法在本题无法通过。

所以大家就当训练思路。

方法二：

这一个方法，就是高傲的数学解法了，我们直接看原理：

我们以示例 1 中 nums = [1,2,3,4,5,6,7]，k = 3 为例，逐步骤、逐元素拆解 “三次反转” 实现数组轮转的过程，彻底理解其原理：

原始状态：明确目标

原始数组：nums = [1,2,3,4,5,6,7]（索引 0~6 对应元素 1~7）。
目标（向右轮转 3 位）：让最后 3 个元素 5,6,7 移到数组最前面，其余元素 1,2,3,4 跟在后面，即最终数组 [5,6,7,1,2,3,4]。

步骤 1：整体逆置（翻转整个数组）

逆置操作是 “将数组首尾元素依次交换，直到中间位置”。

执行过程：

索引 0（元素 1）与索引 6（元素 7）交换 → 数组变为 [7,2,3,4,5,6,1]；
索引 1（元素 2）与索引 5（元素 6）交换 → 数组变为 [7,6,3,4,5,2,1]；
索引 2（元素 3）与索引 4（元素 5）交换 → 数组变为 [7,6,5,4,3,2,1]。

结果与原理：

逆置后数组：[7,6,5,4,3,2,1]。

原本在末尾的 3 个元素（5,6,7），现在被移动到了数组的前半段（前 3 位是 7,6,5），但顺序是 “反向” 的（我们需要的是 5,6,7，现在是 7,6,5）；
原本在前面的 4 个元素（1,2,3,4），现在被移动到了数组的后半段（后 4 位是 4,3,2,1），顺序也是 “反向” 的（我们需要的是 1,2,3,4，现在是 4,3,2,1）。

步骤 2：前 `k` 个元素逆置（翻转前 3 个元素）

对 “整体逆置后数组的前 k 个元素”（即前 3 个元素 7,6,5）执行逆置。

执行过程：

索引 0（元素 7）与索引 2（元素 5）交换 → 数组变为 [5,6,7,4,3,2,1]；
索引 1（元素 6）位置不变（中间位置无需交换）。

结果与原理：

逆置后数组：[5,6,7,4,3,2,1]。

前 3 个元素从 “反向的 7,6,5” 被修正为 “正确顺序的 5,6,7”—— 这正是我们需要 “轮转至前面” 的部分，现在已经到位。

步骤 3：后 `n - k` 个元素逆置（翻转后 4 个元素）

对 “整体逆置后数组的后 n - k 个元素”（n=7，k=3，所以后 7-3=4 个元素 4,3,2,1）执行逆置。

执行过程：

索引 3（元素 4）与索引 6（元素 1）交换 → 数组变为 [5,6,7,1,3,2,4]；
索引 4（元素 3）与索引 5（元素 2）交换 → 数组变为 [5,6,7,1,2,3,4]。

结果与原理：

逆置后数组：[5,6,7,1,2,3,4]。

后 4 个元素从 “反向的 4,3,2,1” 被修正为 “正确顺序的 1,2,3,4”—— 这正是原本在 5,6,7 前面的部分，现在也回到了正确位置。

原理总结：分阶段修正顺序

三次反转的核心是 **“分阶段调整元素的整体位置和内部顺序”**：

整体逆置：先把 “要移动的末尾段” 和 “其余段” 的整体位置互换（但内部顺序反向）；
前 k 个逆置：修正 “要移动的末尾段” 的内部顺序，让其符合目标；
后 n - k 个逆置：修正 “其余段” 的内部顺序，让其符合目标。

最终，无需额外数组（空间复杂度 O(1)），仅通过三次 “线性反转”（每次反转时间复杂度 O(m)，m 为反转段长度，总时间复杂度 O(n)），就完成了数组的轮转。

大家能理解就理解，如果理解不了的话就死记硬背，问题不大，在这里我主要是告诉大家如何用代码实现这一方法。

首先，因为我们要进行逆置，所以我们首先要有逆置函数，那么逆置函数要怎么写呢？

而且要注意，我们的逆置函数还得是一定范围内的逆置，并不是直接全部从头到尾逆置，所以，我们就得设置参数，指定逆置开始的地方和结束的地方，这么一来，我们就能指定到一定的范围，当然，我们还要把数组传进去，由此一来，我们的逆置函数的参数就设置的差不多了。

那么函数内部要怎么写呢？其实也不难，逆置逆置，就是比如把12345，逆置为54321，那我们对比这两个数组，是不是原本的5的位置后面变成了1，而原本的1的位置后面变成了5呢，而碰巧的是，原本的1对应的，正是begin，而原本的5对应的，正是end，所以，其实就是把begin和end所对应的数据进行对换即可，不断对换，直到换无可换，那么怎么才能判定换无可换呢？

其实很明显，那就是当我们的begin和end所对应的数据是相同的时候，也就是begin和end相等了，那么这个时候肯定就是换无可换了，我给大家一个例子：

例子：逆置数组的某一段

假设我们有数组 arr = [1, 2, 3, 4, 5]，现在要逆置从索引 begin = 1 到索引 end = 3 的部分（对应元素 2, 3, 4）。

逆置函数的逻辑步骤

初始状态：begin = 1，end = 3，数组为 [1, 2, 3, 4, 5]。
第一次交换：交换 begin（索引 1，元素 2）和 end（索引 3，元素 4）的元素。
- 交换后数组变为 [1, 4, 3, 2, 5]。
- 然后 begin += 1（变为 2），end -= 1（变为 2）。
判断是否继续：此时 begin == end（都为 2），满足 “换无可换” 的条件，逆置结束。

最终结果

逆置后的数组为 [1, 4, 3, 2, 5]，原本索引 1 到 3 的元素 2, 3, 4 被逆置为 4, 3, 2，而数组其他部分（索引 0 的 1 和索引 4 的 5）保持不变。

再举一个 “换无可换” 更直观的例子

如果要逆置数组 arr = [1, 2, 3] 中 begin = 1 到 end = 1 的部分（只有元素 2）。

因为 begin == end，直接结束逆置，数组保持 [1, 2, 3] 不变，符合 “单个元素逆置后还是自身” 的逻辑。

通过这两个例子可以看到，范围逆置函数通过双指针（begin 和 end）向中间靠拢并交换元素的方式，实现了指定区间内的逆置，且当 begin >= end 时停止，保证了逆置的高效性和正确性。

由此，我们的逆置函数就出来了：

void reverse(int* arr,int begin,int end)
{while(begin<end){int temp=arr[begin];arr[begin]=arr[end];arr[end]=temp;begin++;end--;}
}

大家一定要记得begin++和end--哦。

那么在主函数中，我们就可以调用函数去进行三次逆置了。

那么随之而来，就又有一个问题了，我们的begin和end要是多少呢？因为数组是从0开始存储的，而numsSize又是数组中的数据个数总数，换句话说就是，数组中的numsSize下标是没有数据的。

所以这对我们的什么前k个逆置，后k个逆置有了麻烦，因为我们知道，我们所设计的逆置函数中的begin和end所指向的数组数据，都得是有效的，所以，这同样要求我们极高的确定性以及谨慎性，不难就会导致程序崩溃。

那么对于这个问题，其实大家大可不必担心，我们画图去分析不就知道了吗，大家要谨记，数据结构这一块，画图至关重要，看图：

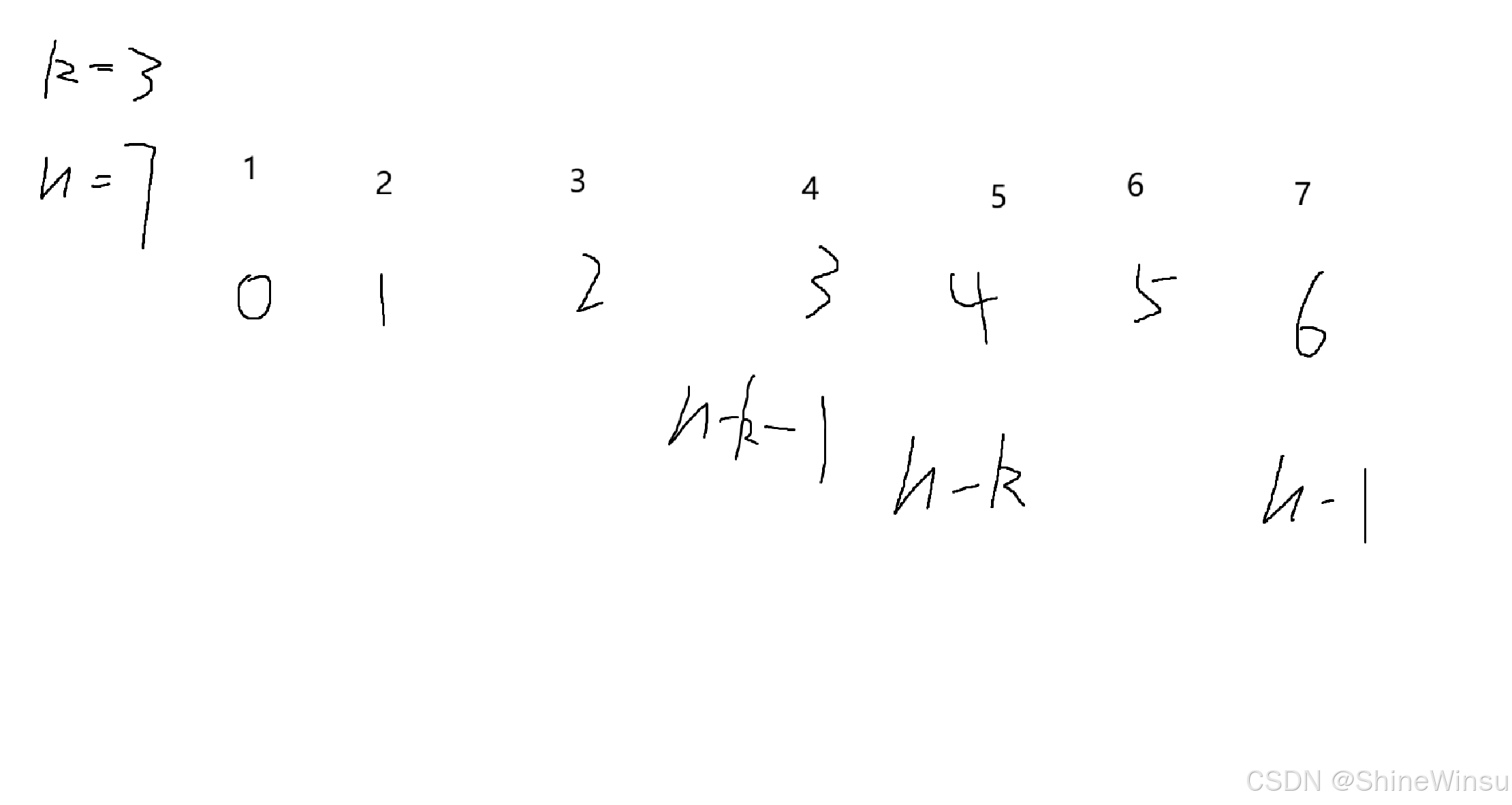
首先我们看三段逆置的第一段：

• 前n-k个逆置：4 3 2 1 5 6 7

这一个我们传进逆置函数的参数要是多少呢，首先，我们要确定begin是哪里，这一段要求我们将-前n-k个逆置，那么也就是7-3=4个数字进行逆置，那么很显然，begin定位在数组的第一个数据，也就是下标为0，即begin=0

那么end呢？它要为多少呢？观察4 3 2 1 5 6 7，很显然，end应该定位在数据4的下标上，而4的下标是3，那么3和n和k什么关系呢？图中我已经给了出来，就是n-k-1，所以，第一段的end就要是n-k-i，即：

reverse(nums,0,n-k-1);

• 后k个逆置：4 3 2 1 7 6 5

那么这一段逆置的begin和end又要是多少呢？我们依旧看图说话，对了，这里要提醒一下大家，我们的第二段逆置是在上面的第一顿逆置之后形成的数组的基础上进行逆置的，这点希望大家注意一些。

可以看到，这一段要求我们把数组的后k个进行逆置，那么end也就很容易确定了，它就是numsSize-1,（大家要记得end指向的数据要是有效的哦）。

那么begin呢？又要是多少呢？我们依旧看图，可以看到在这个例子中，begin是要从5开始的，而它对应的下标是4，而它和n和k的关系又是什么呢？图中依然有，那就是n-k，由此，我们的end也就再次确定下来。

这第二段就是：

reverse(nums,n-k,n-1);

• 整体逆置：5 6 7 1 2 3 4

这最后一段就不需要我们多说了吧各位，begin和end随手就能确定，即：

reverse(nums,0,n-1);

自此，我们的方法二大功告成，下面看完整代码：

// 辅助函数：反转数组中从begin到end（包含两端）的元素
void reverse(int* nums, int begin, int end) {while (begin < end) {// 交换首尾元素int temp = nums[begin];nums[begin] = nums[end];nums[end] = temp;// 向中间移动指针begin++;end--;}
}// 主函数：将数组向右轮转k个位置
void rotate(int* nums, int numsSize, int k) {int n = numsSize;// 处理k大于数组长度的情况，轮转n次相当于没有轮转k = k % n;// 第一次反转：反转前n-k个元素reverse(nums, 0, n - k - 1);// 第二次反转：反转后k个元素reverse(nums, n - k, n - 1);// 第三次反转：反转整个数组reverse(nums, 0, n - 1);
}

方法三：

其实这个方法三，也是用空间换时间的方法，因为大家其实比较难想到方法二，但是方法三可就好想多了。

具体是个什么呢？其实很简单，那就是我们创建一个新数组，然后把原数组中的后k个放在新数组的前面，而原数组的前n-k个就放在新数组的后面，这么一来，不就可以完美解决翻转问题吗，我们看一个例子：

例子：原始数组与目标

假设原始数组 nums = [1, 2, 3, 4, 5, 6, 7]，需要向右轮转 k = 3 个位置。

按照 “方法三” 的思路：

新建一个和原数组长度相同的数组 newNums；
将原数组的后 k 个元素（即 5, 6, 7）放到新数组的前面；
将原数组的前 n - k 个元素（n 是数组长度，这里 n = 7，所以 n - k = 4，即 1, 2, 3, 4）放到新数组的后面；
最后将新数组的内容复制回原数组。

步骤拆解

步骤 1：确定各部分元素

原数组后 k = 3 个元素：索引 4、5、6 对应的元素 5、6、7；
原数组前 n - k = 7 - 3 = 4 个元素：索引 0、1、2、3 对应的元素 1、2、3、4。

步骤 2：填充新数组 newNums

新数组的前 3 个位置（索引 0、1、2）：依次放入原数组后 3 个元素 5、6、7 → newNums = [5, 6, 7, ...]；
新数组的后 4 个位置（索引 3、4、5、6）：依次放入原数组前 4 个元素 1、2、3、4 → newNums = [5, 6, 7, 1, 2, 3, 4]。

步骤 3：复制回原数组

将 newNums 中的元素逐个复制到原数组 nums 中，最终原数组变为 [5, 6, 7, 1, 2, 3, 4]，完成轮转。

另一个例子（小数据量验证）

假设原始数组 nums = [1, 2, 3]，需要向右轮转 k = 1 个位置。

原数组后 k = 1 个元素：3；
原数组前 n - k = 3 - 1 = 2 个元素：1、2；
新数组 newNums 填充后：[3, 1, 2]；
复制回原数组后，nums 变为 [3, 1, 2]，符合 “向右轮转 1 个位置” 的预期。

核心逻辑总结

“方法三” 的本质是用额外的数组空间，直接按 “目标顺序” 重新组织元素：

后 k 个元素需要 “移到前面”，所以放在新数组开头；
前 n - k 个元素需要 “跟在后面”，所以放在新数组末尾；
最后将新数组的结果覆盖原数组，完成轮转。

最后，大家要记得把新数组的数据按顺序全部赋值给原数组哦，因为我们做题时是不返回数据的，也就是力扣是直接检测原数组nums的。

那么关于后k个和前n-k个的起始、终止要定位在哪里，我们在方法二中有讲解，我们这里就不啰嗦，直接看代码：

void rotate(int* nums, int numsSize, int k) {int n = numsSize;// 处理k大于数组长度的情况，避免无效轮转k = k % n;// 创建与原数组同长度的新数组int* arr = (int*)malloc(n * sizeof(int));int sign = 0;  // 新数组的索引指针// 第一步：将原数组后k个元素放入新数组的前面for (int i = n - k; i < n; i++) {arr[sign++] = nums[i];}// 第二步：将原数组前n-k个元素放入新数组的后面for (int i = 0; i < n - k; i++) {arr[sign++] = nums[i];}// 第三步：将新数组的内容复制回原数组for (int i = 0; i < n; i++) {nums[i] = arr[i];}// 释放动态分配的内存，避免内存泄漏free(arr);
}

由此，我们对这两道题目的解析便大功告成。

结语：在 “拆解” 与 “优化” 中，读懂算法的本质

亲爱的朋友们，当我们把 “消失的数字” 和 “轮转数组” 这两道题的多种解法逐一拆解、对比后，这趟从 “理论概念” 到 “实战应用” 的算法之旅，也终于迎来了收尾的时刻。回顾这一路的思考，我们其实不只是在 “做题”，更是在感受算法设计中最核心的逻辑 —— 如何在 “时间” 与 “空间” 的约束下，找到更优的解决方案。

还记得最初面对 “消失的数字” 时，我们最先想到的是 “排序后找空缺” 的直观思路。可当我们计算出它 O (n²) 的时间复杂度时，便会发现这种方法虽然容易理解，却完全无法满足题目对效率的要求。这就像生活中 “用蛮力解决问题”，看似直接，却往往在复杂场景下显得力不从心。而当我们转向 “数学求和” 与 “异或运算” 时，思路一下子就打开了：前者借助等差数列的特性，用两次线性遍历实现了 O (n) 的时间复杂度；后者则利用异或 “相同抵消、0 不变” 的特殊性质，不仅保持了 O (n) 的时间效率，还彻底避免了大数字溢出的风险，空间复杂度更是低至 O (1)。这两种解法让我们明白，算法的优化往往始于对问题本质的深挖—— 当我们跳出 “逐个对比” 的固有思维，看到 “0 到 n 的完整集合” 与 “缺失一个元素的数组” 之间的关系时，更优的方案自然会浮现。

而在 “轮转数组” 的解题过程中，我们又体验了另一种思维的碰撞。“三次反转法” 无疑是最考验巧思的：它没有借助任何额外空间，而是通过 “整体逆置→前 k 个逆置→后 n-k 个逆置” 的三步操作，将 “末尾元素移到前面” 的需求，转化为对元素顺序的分阶段修正。起初我们可能会困惑 “为什么这样反转就能得到结果”，但当我们逐元素拆解每一步的变化后，便会惊叹于这种思路的精妙 —— 它就像用最少的 “动作”，完成了最复杂的 “排列”，完美诠释了 “原地算法” 的高效与优雅。而 “空间换时间” 的新数组法则提供了另一种视角：当我们暂时放下 “极致空间” 的约束，用一个临时数组直接按目标顺序重组元素时，代码逻辑会变得异常直观，这种 “牺牲部分空间换取思路简洁” 的策略，也让我们懂得算法的选择从来不是 “非黑即白”，而是根据实际场景的权衡—— 如果题目对空间复杂度要求不高，这种直观的解法反而能减少出错的可能，提高编码效率。

其实，学习算法的过程，就像在不断打磨一把 “解决问题的钥匙”。我们会遇到看似复杂的问题，会陷入 “想不出思路” 的困境，也会在多种解法中纠结犹豫。但每一次对复杂度的分析、每一次对解法的优化、每一次对思路的复盘，都是在为这把 “钥匙” 增添新的齿痕，让它能应对更多样的 “锁芯”。比如今天我们掌握的 “异或运算”“三次反转”“空间换时间” 这些思路，未来在面对 “寻找重复元素”“字符串翻转” 等问题时，都可能成为解题的关键；而 “一题多解、多解比优” 的思维习惯，更会让我们在遇到陌生问题时，能从不同角度切入，找到最适合的解决方案。

最后，想跟大家说：算法学习从来不是一蹴而就的，它需要我们在理解概念后多动手实践，在写出代码后多复盘优化，在遇到瓶颈时多查阅思考。也许现在的你还会对某些思路感到陌生，还会在编码时出现疏漏，但请相信，每一次对算法的深入思考，都是在为自己的编程能力打下坚实的基础。未来，当我们再面对更复杂的算法问题时，回头看看今天拆解过的这些题目、梳理过的这些思路，一定会感谢此刻认真思考的自己。

那么，这篇博客的内容就到这里了。希望这两道题的解析，能让你对复杂度分析有更具体的认知，对算法设计有更深入的理解。接下来，不妨试着用今天学到的思路，去解决更多类似的问题，在实践中巩固所学、拓展思维。我们下次博客再见，愿你在算法的世界里，始终保持好奇，不断收获成长！

查看全文

http://www.dtcms.com/a/463224.html