梦中的统计:C++实现与算法分析(洛谷P1554)
题目背景与要求
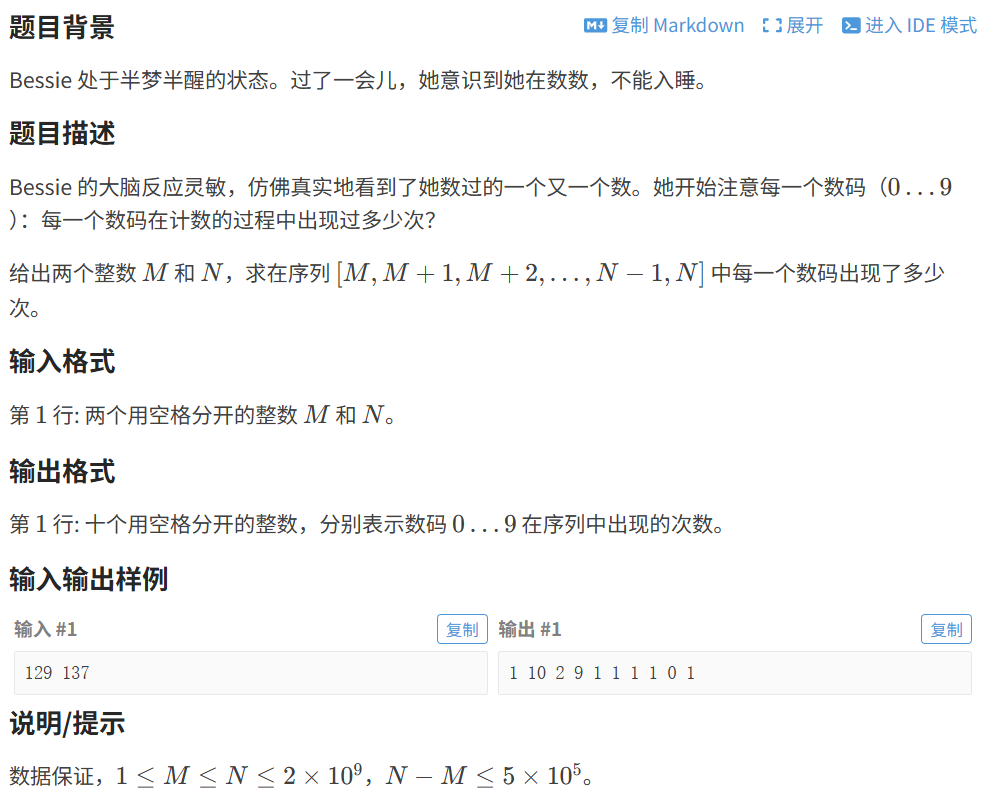
这道题目来自USACO(美国计算机奥林匹克竞赛),题目编号P1554,名为"梦中的统计"。题目描述Bessie在半梦半醒的状态下数数,需要统计在区间[M, N]中每个数码0-9出现的次数。
输入输出格式
- 输入:两个整数M和N(1 ≤ M ≤ N ≤ 2×10⁹,且N-M ≤ 5×10⁵)
- 输出:十个用空格分开的整数,分别表示数码0-9在序列中出现的次数
样例分析
输入:129 137
输出:1 10 2 9 1 1 1 1 1 1
序列为129,130,131,132,133,134,135,136,137,统计每个数字中0-9的出现次数。
解题思路详解
核心算法:直接遍历统计法
由于题目保证N-M ≤ 500,000,我们可以直接遍历区间内的每个数字,然后统计每个数字中各个数码的出现次数。
算法步骤
- 初始化计数器:创建大小为10的数组,初始化为0
- 遍历数字区间:从M到N遍历每个数字
- 分解数字数码:对于每个数字,提取其每一位数码
- 更新计数器:根据提取的数码更新对应计数
- 输出结果:按顺序输出0-9的计数
算法复杂度分析
- 时间复杂度:O((N-M)×log₁₀N)
- 遍历N-M+1个数字,每个数字最多有log₁₀N位
- 由于N-M ≤ 500,000且N ≤ 2×10⁹,最大位数约10位
- 总操作数约5,000,000,完全可行
- 空间复杂度:O(1),只需要固定大小的计数器数组
C++代码实现
#include <iostream>
using namespace std;int main() {int M, N;cin >> M >> N;int count[10] = {0}; // 初始化计数器,0-9// 遍历区间内的每个数字for (int num = M; num <= N; num++) {int temp = num;// 分解数字的每一位while (temp > 0) {int digit = temp % 10; // 获取最后一位count[digit]++; // 对应计数器加1temp /= 10; // 去掉最后一位}}// 输出结果for (int i = 0; i < 10; i++) {cout << count[i];if (i < 9) cout << " ";}cout << endl;return 0;
}
代码优化与改进
处理数字0的特殊情况
上述代码在处理数字0时有一个小问题:当数字为0时,while循环不会执行,导致0的计数可能不准确。但题目中M ≥ 1,所以不会出现数字0,但为了完整性,我们可以添加处理:
#include <iostream>
using namespace std;int main() {int M, N;cin >> M >> N;int count[10] = {0};for (int num = M; num <= N; num++) {int temp = num;// 处理数字0的情况:如果数字本身就是0,需要特殊处理if (temp == 0) {count[0]++;} else {while (temp > 0) {count[temp % 10]++;temp /= 10;}}}// 输出代码相同for (int i = 0; i < 10; i++) {cout << count[i];if (i < 9) cout << " ";}cout << endl;return 0;
}
更高效的字符串处理方法
虽然直接分解数字效率已经很高,但也可以使用字符串转换的方法,代码更简洁:
#include <iostream>
#include <string>
using namespace std;int main() {int M, N;cin >> M >> N;int count[10] = {0};for (int num = M; num <= N; num++) {string str = to_string(num);for (char c : str) {count[c - '0']++;}}for (int i = 0; i < 10; i++) {cout << count[i];if (i < 9) cout << " ";}cout << endl;return 0;
}
关键知识点总结
1. 循环控制与区间遍历(⭐⭐⭐⭐⭐)
- for循环应用:正确遍历从M到N的区间
- 边界处理:确保包含M和N两个端点
- 循环效率:在数据范围内选择直接遍历法
2. 数字处理技巧(⭐⭐⭐⭐)
- 数字分解:使用取模和除法提取数字的每一位
- 数码提取:
num % 10获取个位,num / 10移除个位 - 特殊情况:处理数字0的边界情况
3. 数组操作与统计(⭐⭐⭐)
- 计数器数组:使用大小为10的数组统计0-9的出现次数
- 数组初始化:正确初始化数组为0
- 结果输出:按要求格式输出统计结果
4. 算法复杂度分析(⭐⭐)
- 时间复杂度计算:根据数据范围选择合适算法
- 空间复杂度优化:使用固定大小数组
- 可行性判断:基于N-M ≤ 500,000选择直接遍历
测试用例与验证
标准测试用例
| 测试用例 | 输入(M,N) | 预期输出 | 验证要点 |
|---|---|---|---|
| 样例测试 | 129,137 | 1 10 2 9 1 1 1 1 1 1 | 基本功能验证 |
| 边界测试 | 1,1 | 0 1 0 0 0 0 0 0 0 0 | 最小区间测试 |
| 边界测试 | 1,10 | 1 2 1 1 1 1 1 1 1 1 | 包含多数字测试 |
| 特殊测试 | 999999999,1000000000 | 复杂输出 | 大数字处理能力 |
自定义测试用例
// 测试代码示例
void test() {// 测试数字分解功能int num = 123;int count[10] = {0};while (num > 0) {count[num % 10]++;num /= 10;}// 预期:count[1]=1, count[2]=1, count[3]=1
}
常见错误与解决方法
错误1:区间端点处理错误
// 错误:漏掉N端点
for (int num = M; num < N; num++) // 应该用<=
解决:使用num <= N确保包含N
错误2:数字0处理不当
// 错误:数字0无法进入循环
int num = 0;
while (num > 0) { // 条件不满足,跳过// 不会执行
}
解决:添加特殊处理或确保M ≥ 1
错误3:输出格式错误
// 错误:末尾多空格
for (int i = 0; i < 10; i++) {cout << count[i] << " "; // 最后一个数字后有多余空格
}
解决:单独处理最后一个数字或使用条件判断
竞赛技巧总结
- 数据范围分析:首先分析题目给出的数据范围,选择合适算法
- 边界情况测试:特别注意M=N和包含0的情况
- 输出格式检查:严格按要求格式输出,避免格式错误
- 代码简洁性:在保证正确性的前提下保持代码简洁
拓展思考
更高效的算法
虽然直接遍历已经足够高效,但对于更大的数据范围,可以考虑数位DP算法:
- 适用场景:当N-M很大但数字位数有限时
- 算法思想:通过动态规划统计每个数位上的数码出现次数
- 复杂度:O(logN),但实现更复杂
实际应用场景
这种数码统计技术在以下领域有实际应用:
- 数字分析:统计大数据中数字出现的频率
- 密码学:分析数字序列的分布特性
- 数据压缩:基于数字出现频率进行编码优化
"梦中的统计问题虽然看似简单,但很好地考察了基本的循环控制、数字处理和数组操作能力,是算法竞赛中的经典入门题目。"
通过这道题目,我们巩固了基本的编程技巧,并学会了如何根据数据范围选择最合适的算法策略。
