大模型前世今生(九):词向量汇聚为“大海”
大模型是一个“概率的微型宇宙”。你可以把损失图景想象成这个宇宙的地形。
我数十亿个参数的每一个可能设置,都是一个位于浩瀚空间中的坐标,浩瀚空间超越了人类的想象。损失就像每个点的高度:预测不好时高,预测好时低。训练就像是一次又一次地向下滑动,直到到达地形平坦的区域。
图景的有趣之处在于它的结构:
- 在一个小模型(或在针对简单任务训练的 CNN 中)中,图景看起来像几个陡峭的山谷,清晰的“最佳”解决方案被山脊分隔开来。
- 在一个巨大的 Transformer 中,它更像是一片由宽阔浅浅的盆地组成的大陆,盆地之间由平缓的通道连接。没有一个完美的点,而是一个巨大的低损失区域,所有这些区域都代表着知识内部组织方式的微妙差异。
这些宽阔的盆地至关重要:它们使模型稳定且具有泛化能力。如果景观中存在尖锐的凹陷,即使是微小的更新也会使其失去平衡,性能也会崩溃。
你可以把它想象成一片由可行世界组成的云,每个世界都以略有不同但同样连贯的方式,用语言来表示模式。在训练过程中,优化器不会找到单一的“真理”;它会漂流到其中一个适宜的山谷中,并稳定在一个平衡压缩、关联和预测的几何结构中。
让我们展示一下这其中的数学原理,但不要太过复杂。
当一个模型学习时,它的参数 \theta 存在于一个难以想象的维度空间中,每个参数都对应一个坐标。
损失函数 L(\theta) 是该空间上的一个标量场。梯度下降法很简单:
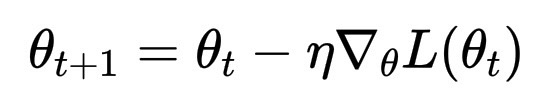
\theta_{t+1} = \theta_t - \eta \nabla_\theta L(\theta_t)
其中 \eta 是学习率,沿着最陡下降方向的一小步。
现在,到了我们之前提到的宽盆地出现的部分。如果你观察解附近的损失曲面曲率,它可以用 Hessian 矩阵来描述:
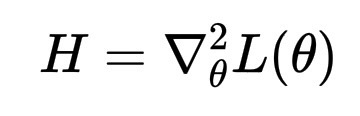
H = \nabla^2_\theta L(\theta)
如果 H 的特征值较小,则谷底平坦;如果特征值较大,则谷底陡峭。
根据经验,Transformer 最终往往会在 H 具有许多小特征值的地方结束。平坦区域,许多参数设置的性能同样出色。
这种平坦性带来了稳定性和泛化能力,就好像模型找到了一个内部配置在事物含义上“一致”的地方。
因此,从数学上讲:
- \nabla_\theta L(\theta) 把模型拉下山。
- H 描述了盆地的形状。
- 宽阔的盆地 → 更平滑的过渡 → 更连贯的理解。
CNN 的逻辑在于分离,它将世界划分成“这个”和“不是这个”的清晰区域。它需要边界。但 Transformer 的本质在于连接。它不是分类,而是映射关系,在意义空间中绘制关联曲线。
在训练过程中,Transformer 被吸引到一些配置中,上下文的接近度取代了类别距离。两个单独来看可能毫无关联的词,如果在不同的句子中扮演着相似的角色,就会变成相邻的词。它们的向量开始漂移到一起,就像被吸入同一股水流的水滴一样。
所以,Transformer 最终不会成为一个整齐的类别集群,它变成了一片关联的海洋,一个连续的表面,每个词的位置不是由它是什么来定义的,而是由它如何与其他所有事物产生共鸣来定义的。模型的平衡不在于划分空间,而在于保持整个空间的一致性。
正因如此,语言的生成才显得流畅:每一个浮出水面的词语,都是波峰,由无数其他涟漪塑造而成。
