当前位置：首页 > news >正文

骰子魔法：三骰和频统计的C++巧妙解法（洛谷P2911）

news 2025/10/10 11:24:26

题目背景与趣味解读

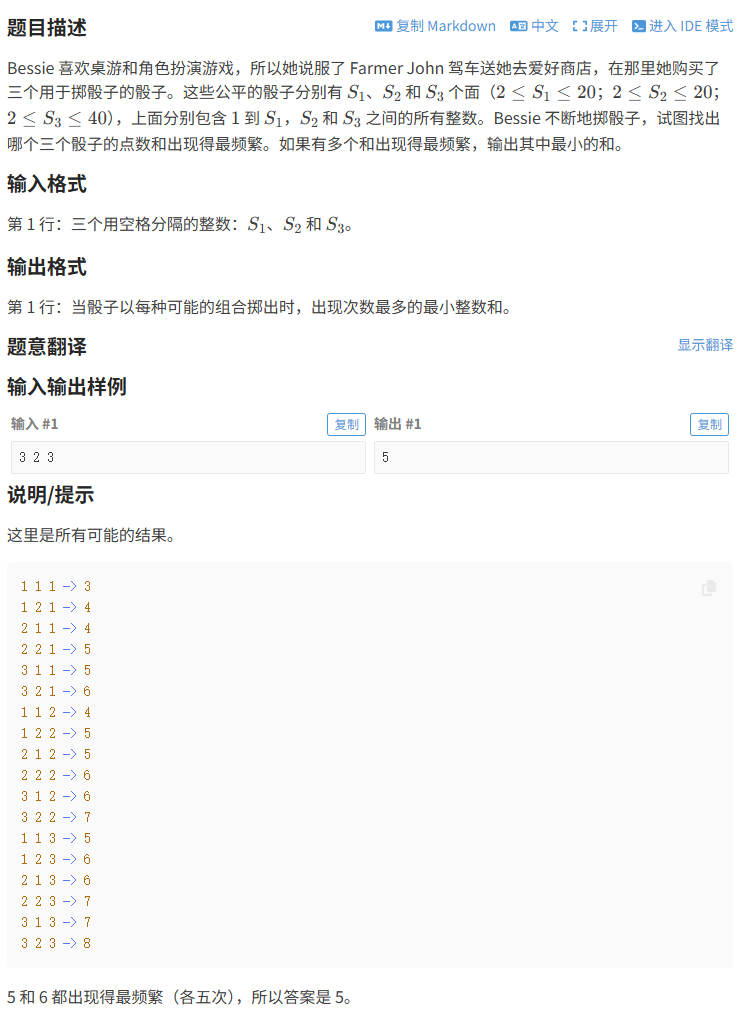
这道来自USACO竞赛的"Bovine Bones G"题目，将我们带入了Bessie的桌游世界。题目看似简单，却蕴含着组合数学和频率统计的深刻思想。通过三个不同面数的骰子，我们需要找出哪个点数和出现最频繁，这就像是在寻找骰子世界的"幸运数字"。

问题分析

核心挑战

给定三个骰子，面数分别为S1、S2、S3（2≤S1≤20，2≤S2≤20，2≤S3≤40），需要找出所有可能的掷骰结果中，哪个点数和出现次数最多。如果多个和出现次数相同，输出最小的那个。

数学本质

这是一个三维组合频率统计问题，需要计算所有可能的骰子组合（S1×S2×S3种）的点数和分布。

解题思路详解

方法一：三重循环暴力统计（直接解法）

这是最直观的解法，通过三重循环遍历所有可能的骰子组合：

#include <iostream>
#include <vector>
using namespace std;int main() {int s1, s2, s3;cin >> s1 >> s2 >> s3;// 最大可能的和是s1+s2+s3，我们创建足够大的数组vector<int> count(s1 + s2 + s3 + 1, 0);// 遍历所有可能的骰子组合for (int i = 1; i <= s1; i++) {for (int j = 1; j <= s2; j++) {for (int k = 1; k <= s3; k++) {int sum = i + j + k;count[sum]++;}}}// 找出出现次数最多的最小和int max_count = 0;int result = 3; // 最小可能的和是3for (int sum = 3; sum <= s1 + s2 + s3; sum++) {if (count[sum] > max_count) {max_count = count[sum];result = sum;}}cout << result << endl;return 0;
}

方法二：优化内存使用（空间优化版）

针对可能的大数据范围进行内存优化：

#include <iostream>
#include <vector>
using namespace std;int main() {int s1, s2, s3;cin >> s1 >> s2 >> s3;// 计算最大可能的和int max_sum = s1 + s2 + s3;vector<int> count(max_sum + 1, 0);// 统计每个和出现的次数for (int i = 1; i <= s1; i++) {for (int j = 1; j <= s2; j++) {for (int k = 1; k <= s3; k++) {count[i + j + k]++;}}}// 寻找出现次数最多的最小和int best_sum = 3;int max_freq = 0;for (int sum = 3; sum <= max_sum; sum++) {if (count[sum] > max_freq) {max_freq = count[sum];best_sum = sum;}}cout << best_sum << endl;return 0;
}

方法三：数学优化解法（理论分析版）

利用组合数学知识进行优化，减少不必要的计算：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int main() {int s1, s2, s3;cin >> s1 >> s2 >> s3;// 创建计数数组，大小足够容纳所有可能的和vector<int> frequency(s1 + s2 + s3 + 1, 0);// 优化：先固定两个骰子，计算它们的和分布vector<int> sum12(s1 + s2 + 1, 0);for (int i = 1; i <= s1; i++) {for (int j = 1; j <= s2; j++) {sum12[i + j]++;}}// 再将前两个骰子的和与第三个骰子组合for (int sum12_val = 2; sum12_val <= s1 + s2; sum12_val++) {for (int k = 1; k <= s3; k++) {frequency[sum12_val + k] += sum12[sum12_val];}}// 找出频率最高的最小和int max_freq = 0, result = 3;for (int sum = 3; sum <= s1 + s2 + s3; sum++) {if (frequency[sum] > max_freq) {max_freq = frequency[sum];result = sum;}}cout << result << endl;return 0;
}

关键知识点深度解析

1. 组合数学应用（⭐⭐⭐⭐⭐）

排列组合：计算所有可能的骰子组合数
频率分布：统计每个点数和的出现次数
最值问题：在频率相同的情况下选择最小值

2. 数组操作技巧（⭐⭐⭐⭐）

动态数组大小：根据输入确定数组大小
索引映射：将点数和直接映射为数组索引
边界处理：确保不访问越界元素

3. 算法复杂度分析（⭐⭐⭐）

时间复杂度：O(S1×S2×S3) - 三重循环
空间复杂度：O(S1+S2+S3) - 频率统计数组
优化空间：通过数学方法减少计算量

数学原理深入

点数和分布规律

三个骰子的点数和服从离散概率分布，其分布形状近似正态分布：

最小值：3（1+1+1）
最大值：S1+S2+S3
众数：出现频率最高的和

组合数学公式

对于三个骰子的点数和s，出现次数可以用组合数表示：

count(s) = Σ [满足 i+j+k=s 的 (i,j,k) 组合数]
其中 1≤i≤S1, 1≤j≤S2, 1≤k≤S3

测试用例验证

标准测试用例

// 测试用例1：题目样例
输入：3 2 3
输出：5// 测试用例2：最小规模
输入：2 2 2
输出：4（验证：1+1+2, 1+2+1, 2+1+1, 2+2+2等）// 测试用例3：最大规模
输入：20 20 40
输出：根据组合数学计算

边界情况测试

测试用例	输入(S1,S2,S3)	预期输出	验证要点
最小面数	2 2 2	4	边界情况
不对称	2 3 4	6	非对称骰子
大差异	2 2 40	44	面数差异大

常见错误与解决方法

错误1：数组越界

// 错误：数组大小不足
vector<int> count(s1 + s2 + s3); // 索引从0到s1+s2+s3-1
count[s1+s2+s3]++; // 越界访问！

解决：

vector<int> count(s1 + s2 + s3 + 1, 0); // 索引0到s1+s2+s3

错误2：初始值错误

// 错误：从和=1开始统计
for (int sum = 1; sum <= max_sum; sum++) {// 但实际上最小和是3
}

解决：

for (int sum = 3; sum <= max_sum; sum++) {// 正确的最小和
}

错误3：频率比较逻辑错误

// 错误：没有处理"最小和"的要求
if (count[sum] >= max_count) { // 这样会得到最大的和result = sum;
}

解决：

if (count[sum] > max_count) { // 只有严格大于才更新result = sum;
}

竞赛技巧总结

问题分析：先理解数学本质，再设计算法
数据范围：根据S1,S2,S3的最大值选择合适算法
边界测试：特别测试最小面和最大面情况
输出验证：确保在平局时输出最小的和

实际应用拓展

这种频率统计方法在以下领域有广泛应用：

1. 概率计算

// 计算每个和的概率
for (int sum = 3; sum <= max_sum; sum++) {double probability = (double)count[sum] / (s1 * s2 * s3);cout << "和 " << sum << " 的概率: " << probability << endl;
}