10.9 lpf|求凸包|正反扫描
lc3494
正向模拟,反向倒推更新
模拟多名巫师按顺序酿造每瓶药水的过程max
用数组记录巫师完成上一瓶的时间
最终算出酿造所有药水的最短总时间

class Solution {
public:
long long minTime(vector<int>& skill, vector<int>& mana) {
int n = skill.size();
vector<long long> last_finish(n); // 第 i 名巫师完成上一瓶药水的时间
for (int m : mana) {
// 按题意模拟
long long sum_t = 0;
for (int i = 0; i < n; i++) {
sum_t = max(sum_t, last_finish[i]) + skill[i] * m;
}
// 倒推:如果酿造药水的过程中没有停顿,那么 lastFinish[i] 应该是多少
last_finish[n - 1] = sum_t;
for (int i = n - 2; i >= 0; i--) {
last_finish[i] = last_finish[i + 1] - skill[i + 1] * m;
}
}
return last_finish[n - 1];
}
};

class Solution {
public:
long long minTime(vector<int>& skill, vector<int>& mana) {
int n = skill.size(), m = mana.size();
vector<int> s(n + 1); // skill 的前缀和
partial_sum(skill.begin(), skill.end(), s.begin() + 1);
long long start = 0;
for (int j = 1; j < m; j++) {
long long mx = 0;
for (int i = 0; i < n; i++) {
mx = max(mx, 1LL * mana[j - 1] * s[i + 1] - 1LL * mana[j] * s[i]);
}
start += mx;
}
return start + 1LL * mana[m - 1] * s[n];
}
};
凸包


struct Vec {
int x, y;
Vec operator-(const Vec& b) { return {x - b.x, y - b.y}; }
long long det(const Vec& b) { return 1LL * x * b.y - 1LL * y * b.x; }
long long dot(const Vec& b) { return 1LL * x * b.x + 1LL * y * b.y; }
};
class Solution {
// Andrew 算法,计算 points 的上凸包
// 由于横坐标(前缀和)是严格递增的,所以无需排序
vector<Vec> convex_hull(vector<Vec>& points) {
vector<Vec> q;
for (auto& p : points) {
while (q.size() > 1 && (q.back() - q[q.size() - 2]).det(p - q.back()) >= 0) {
q.pop_back();
}
q.push_back(p);
}
return q;
}
public:
long long minTime(vector<int>& skill, vector<int>& mana) {
int n = skill.size(), m = mana.size();
vector<int> s(n + 1);
vector<Vec> vs(n);
for (int i = 0; i < n; i++) {
s[i + 1] = s[i] + skill[i];
vs[i] = {s[i], skill[i]};
}
vs = convex_hull(vs); // 去掉无用数据
long long start = 0;
for (int j = 1; j < m; j++) {
Vec p = {mana[j - 1] - mana[j], mana[j - 1]};
// p.dot(vs[i]) 是个单峰函数,二分找最大值
int l = -1, r = vs.size() - 1;
while (l + 1 < r) {
int mid = l + (r - l) / 2;
(p.dot(vs[mid]) > p.dot(vs[mid + 1]) ? r : l) = mid;
}
start += p.dot(vs[r]);
}
return start + 1LL * mana[m - 1] * s[n];
}
};
lc2584
用最小质因数数组来高效处理质因数相关操作,以找到有效的数组分割点
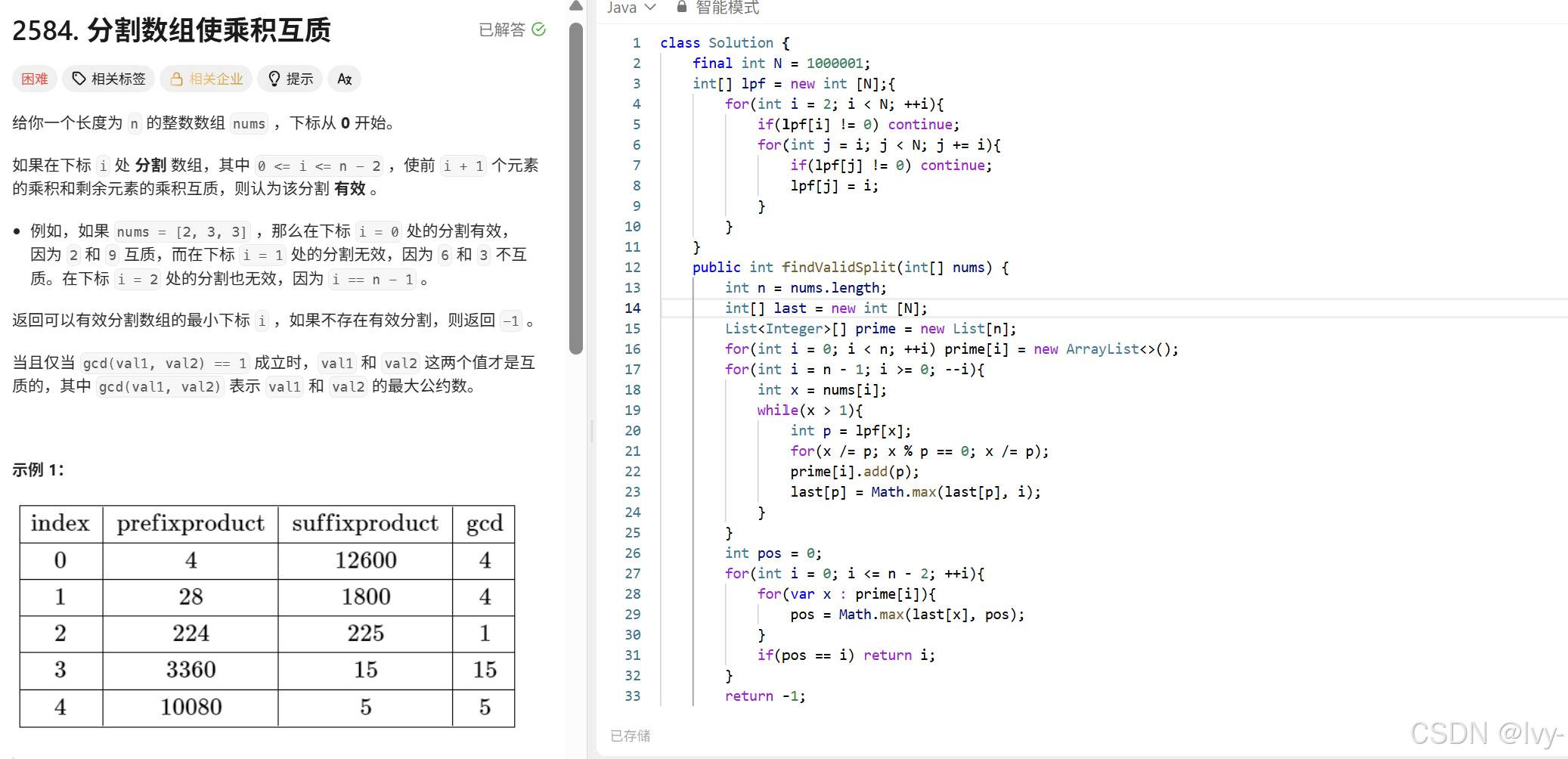
lpf 是 lowest prime factor (最小质因数)的缩写。
代码的前半部分通过一个循环来初始化 lpf 数组。对于每个数 i ,如果 lpf[i] 还没有被赋值(即 lpf[i] == 0 ),就说明 i 是一个质数。
然后,对于 i 的所有倍数 j (从 i 开始,每次增加 i ),如果 lpf[j] 还没有被赋值,就将 lpf[j] 设为 i 。这样, lpf[j] 就存储了 j 的最小质因数。
(和素数筛一个思想)
在后续处理数组元素的质因数时,会用到 lpf 数组来快速分解每个数的质因数。例如,当分解数 x 时,通过不断除以它的最小质因数(从 lpf[x] 获取),可以逐步得到 x 的所有质因数

C++ 的版本:
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
private:
const int N = 1000001;
vector<int> lpf;
void initLPF()
{
lpf.resize(N, 0);
for (int i = 2; i < N; ++i) {
if (lpf[i] != 0) continue;
for (int j = i; j < N; j += i) {
if (lpf[j] != 0) continue;
lpf[j] = i;
}
}
}
public:
int findValidSplit(vector<int>& nums) {
initLPF();
int n = nums.size();
vector<int> last(N, 0);
vector<vector<int>> prime(n);
for (int i = 0; i < n; ++i) {
prime[i] = vector<int>();
}
for (int i = n - 1; i >= 0; --i) {
int x = nums[i];
while (x > 1) {
int p = lpf[x];
while (x % p == 0) {
x /= p;
}
prime[i].push_back(p);
last[p] = max(last[p], i);
}
}
int pos = 0;
for (int i = 0; i <= n - 2; ++i) {
for (int p : prime[i]) {
pos = max(last[p], pos);
}
if (pos == i) {
return i;
}
}
return -1;
}
};
代码说明
1. initLPF 函数:
- 用于初始化最小质因数数组 lpf 。通过双重循环,为每个数找到其最小的质因数。
2. findValidSplit 函数:
- 首先调用 initLPF 初始化 lpf 数组。
- 然后定义 last 数组记录每个质因数最后出现的位置, prime 数组存储每个位置上数字的质因数。
- 从后往前遍历数组 nums ,对每个数字分解质因数,并更新 last 数组和 prime 数组。
- 最后从前向后遍历,根据 prime 和 last 数组寻找有效的分割点。
lc804
hash
class Solution {
public:
int uniqueMorseRepresentations(vector<string>& words) {
// 哈希表法
int len = words.size();
if(len == 0){
return 0;
}
vector<string> datas = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
unordered_set<string> tag;
for(int i = 0; i < len; i ++){
string str;
for(int j = 0; j < words[i].size(); j ++)
{ //转摩斯
char ch = words[i][j];
if(ch >= 'a' && ch <= 'z')
str += datas[ch - 'a'];
else if(ch >= 'A' && ch <= 'Z')
str += datas[ch - 'A'];
else
return -1;
}
tag.insert(str);
}
return tag.size();
}
};
