深度学习优化算法深入分析:从 SGD 到 LAMB
(深度学习入门·进阶篇)
一、前言
在深度学习训练的世界里,优化算法 是模型能否成功学习的核心。
神经网络的本质,是一个巨大的参数空间搜索问题。我们希望找到那组参数,使得模型在训练集与验证集上都能尽可能地拟合数据,同时保持良好的泛化能力。
优化算法的任务,就是在高维非凸空间中,引导模型的参数逐步收敛到一个合理的点。
这听起来抽象,但可以这样理解:
模型训练就像在一座山谷中行走,我们想找到最低点。每一次迭代,就是在地形上迈出一步。优化算法的不同之处在于,它决定了——
“往哪个方向走、走多远、是否该加速、是否该减速、是否该暂缓片刻”。
本篇文章,我们将系统地梳理从 SGD(随机梯度下降) 到 LAMB(Layer-wise Adaptive Moments optimizer for Batching training) 的演化脉络,
并以实际训练经验为落脚点,深入分析它们的数学原理、直觉理解、伪代码结构与适用场景。
二、SGD:最基础也最重要的优化器
2.1 基本思想
最早的优化算法源于梯度下降(Gradient Descent),核心思想非常简单:

其中:
θt\theta_tθt:当前参数;
η\etaη:学习率;
∇θL(θt)\nabla_\theta L(\theta_t)∇θL(θt):当前参数下的损失函数梯度。
梯度告诉我们“往哪个方向上升最快”,所以我们反方向更新参数,让损失下降。
然而,在深度学习中,数据量巨大,无法每次都计算全量梯度。于是我们引入“随机性”:
SGD(Stochastic Gradient Descent,随机梯度下降) 每次仅取一个小批次(batch)来估计梯度。
更新公式变为:
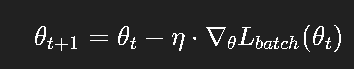
这种方法简单、高效,但也存在两个显著问题:
噪声大:由于每次只用部分样本,梯度方向带有随机性;
收敛慢:在损失面复杂的情况下,容易“抖动”或陷入局部低谷。
2.2 伪代码实现(SGD)
# Pseudocode: Simple SGD
initialize parameters θ randomly
for epoch in range(EPOCHS):for batch in data_loader:grad = compute_gradient(Loss, θ, batch)θ = θ - lr * grad
这段伪代码几乎是所有优化算法的骨架。接下来我们在此基础上,逐步引入各种改进。
三、Momentum:让优化不再“颤抖”
SGD 在陡峭或狭长的损失面上会剧烈震荡。为了解决这个问题,人们引入了动量(Momentum) 概念。
3.1 思路来源
物理直觉上,一个物体在斜坡上滚动时,速度不会突然变成 0,它会保留之前的动量。
在优化中,我们希望让参数更新“具有惯性”,不要每次都完全依赖当前梯度。
公式:
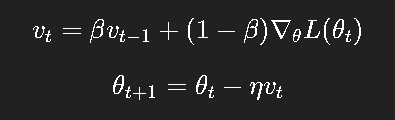
其中:
vtv_tvt:动量项,代表梯度的“历史平均”;
β\betaβ:动量衰减系数(常取 0.9)。
3.2 效果
在平缓方向上,动量叠加能加速收敛;
在震荡方向上,正负梯度相互抵消,抑制抖动。
可以把 Momentum 看作是在 SGD 的基础上加了“惯性系统”。
3.3 伪代码实现(Momentum SGD)
v = 0
for batch in data_loader:grad = compute_gradient(Loss, θ, batch)v = beta * v + (1 - beta) * gradθ = θ - lr * v
动量的引入,让训练更加平滑,但它仍然无法适应不同参数尺度的差异。
这引出了下一位主角——AdaGrad。
四、AdaGrad:自适应学习率的启示
4.1 动机
SGD 和 Momentum 的学习率 η\etaη 是固定的,这导致:
参数变化大的维度,更新过快;
参数变化小的维度,更新过慢。
于是,AdaGrad 提出:为每个参数引入独立的学习率,并根据历史梯度自动调整。
4.2 更新公式
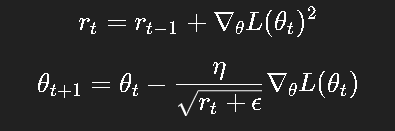
其中:
rtr_trt 是梯度平方的累积和;
分母越大,说明该参数的梯度经常很大,于是自动降低学习率。
4.3 伪代码实现(AdaGrad)
r = 0
for batch in data_loader:grad = compute_gradient(Loss, θ, batch)r += grad ** 2θ -= lr / (sqrt(r) + eps) * grad
4.4 问题与改进方向
AdaGrad 的核心问题是:学习率会不断衰减,最终几乎停止更新。
为了克服这一点,后来出现了 RMSProp。
五、RMSProp:平衡记忆与遗忘
RMSProp(Root Mean Square Propagation)通过指数加权移动平均取代累积和,
让优化器既能记住近期梯度信息,又能逐渐忘记久远的梯度。
5.1 更新公式
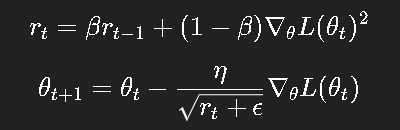
这就像 AdaGrad 的“滑动窗口版本”,不再让学习率无限衰减。
5.2 实践意义
对非平稳目标函数表现良好;
更适用于深度神经网络;
被许多框架(如 TensorFlow)设为默认优化器之一。
六、Adam:实用主义的胜利
2014 年,Kingma 和 Ba 发布了著名的论文《Adam: A Method for Stochastic Optimization》,
该算法几乎成为深度学习的默认选择。
Adam 综合了 Momentum 与 RMSProp 的优点:
既保留一阶矩(动量),又保存二阶矩(平方梯度均值)。
6.1 更新公式
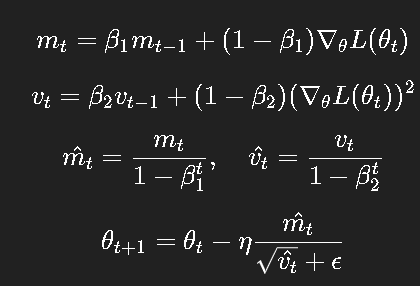
其中:
mtm_tmt:一阶动量;
vtv_tvt:二阶动量;
mt^,vt^\hat{m_t}, \hat{v_t}mt^,vt^:偏差修正版本(用于抵消初始化偏差)。
6.2 Adam 的特性
自动调节学习率;
训练收敛快;
对超参数不敏感(通常 β1=0.9,β2=0.999\beta_1=0.9, \beta_2=0.999β1=0.9,β2=0.999)。
6.3 伪代码实现(Adam)
m, v = 0, 0
for t, batch in enumerate(data_loader, 1):grad = compute_gradient(Loss, θ, batch)m = beta1 * m + (1 - beta1) * gradv = beta2 * v + (1 - beta2) * (grad ** 2)m_hat = m / (1 - beta1 ** t)v_hat = v / (1 - beta2 ** t)θ -= lr * m_hat / (sqrt(v_hat) + eps)
七、AdamW 与 LAMB:大模型时代的优化进化
7.1 AdamW:权重衰减的正确打开方式
在常规 Adam 中,使用 weight_decay 通常等价于给参数添加 L2 正则项。
然而,由于 Adam 有自适应学习率,这种正则化方式会被扭曲。
AdamW(Loshchilov & Hutter, 2017)提出了更合理的权重衰减:
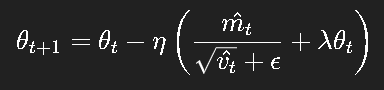
即在梯度更新后直接进行权重衰减,从而保持优化与正则化的独立性。
这使得 AdamW 成为 Transformer、BERT 等模型训练的标准选择。
7.2 LAMB:为大批量训练而生
随着 BERT、GPT 等超大模型的出现,单机显然无法容纳庞大的 batch。
当批次过大时,Adam 的梯度更新方向会被“稀释”,学习率调整失效。
LAMB(Layer-wise Adaptive Moments optimizer for Batch training)
在 Adam 的基础上,对每一层引入了自适应的归一化因子:
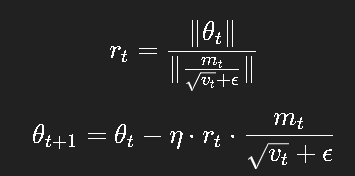
这样,每层都能根据自身权重尺度,动态控制更新步幅。
实践表明,LAMB 在大规模并行训练中显著提升了收敛稳定性。
八、实践经验与调参建议
SGD + Momentum
推荐用于卷积网络(如 ResNet)。
学习率通常较大(0.1 左右),配合学习率衰减。
Adam / AdamW
推荐用于 Transformer、NLP 模型。
默认参数一般就能收敛;但若过拟合,考虑增大 weight decay。
RMSProp
适用于 RNN 或非平稳任务。
与 Adam 相比收敛略慢,但噪声较小。
LAMB / LARS
用于大规模训练(batch ≥ 8192)。
可线性增大学习率以匹配批次扩展。
九、结语
优化算法的历史,其实就是“在噪声与速度之间找平衡”的历史。
从最初的 SGD 到如今的大模型优化器,人们不断地在权衡“收敛稳定性、泛化能力与训练效率”。
没有一种优化器是万能的。
真正的关键是:理解算法背后的思想,知道它“为什么能收敛”、“何时可能失效”,
并在具体任务中灵活选择。
