PID--微分项D

含有比例项、积分项和微分项的PID输出值： 

微分项的输出值取决于当前时刻误差变化的斜率，与当前时刻附近误差变化的趋势有关。当误差急剧变化时，微分项会负反馈输出相反的作用力，阻碍误差急剧变化

斜率一定程度上反映了误差未来的变化趋势，这使得微分项具有 “预测未来，提前调控”的特性

微分项给系统增加阻尼，可以有效防止系统超调，尤其是惯性比较大的系统 K_D越大，微分项权重越大，系统阻尼越大，但系统卡顿现象也会随之增加      

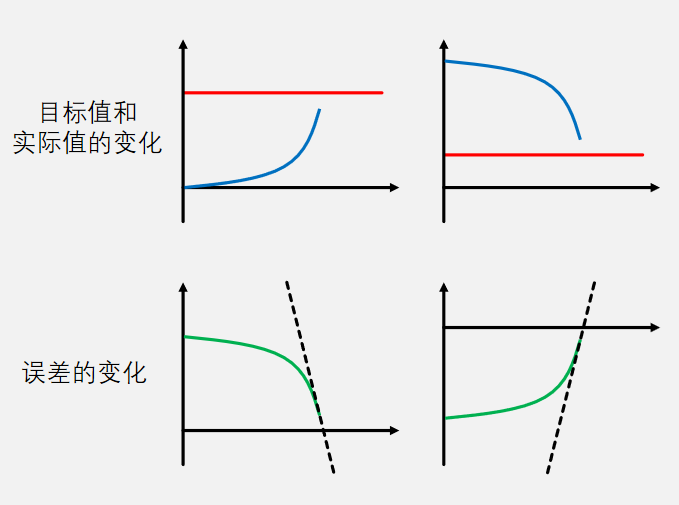微分项K_d∗(error(k)−error(k−1))    受两次误差的差值影响，如果变化过大肯会导致微分项很大。

微分先行

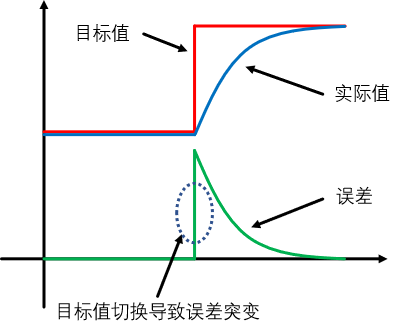如图可知，当我们大幅度调整目标值时，会有一个较大error(k)−error(k−1)微分值出现，这会导致微分项突然输出一个很大的调控力，如果系统的目标值频繁大幅度切换，则此时的微分项不利于系统稳定

微分先行实现思路：将对误差的微分替换为对实际值的微分

普通PID的微分项输出： dout(k)=K_d∗(error(k)−error(k−1))

微分先行PID的微分项输出： dout(k)= − K_d∗(actual(k)−actual(k−1))

把微分项与实际值绑定二维误差值绑定可以消除目标值的影响

Actual1 = Actual;
Actual += Encoder_Get();
Error0 = Target - Actual;
if(K_I != 0){ErrorInt += Error0;}
else{ErrorInt = 0;}
Out = K_P * Error0 + K_I * ErrorInt - K_D * (Actual - Actual1);

不完全微分

要解决的问题：传感器获取的实际值经常会受到噪声干扰，而PID控制器中的微分项对噪声最为敏感，这些噪声干扰可能会导致微分项输出抖动，进而影响系统性能

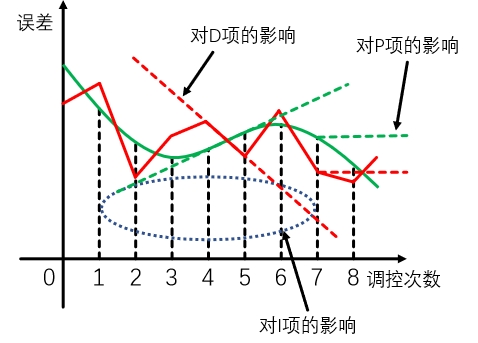有图可见，红色是噪声导致的误差值，绿色是理想情况，噪声对P项影响的的是两线只差，对I项影响的是面积，这两项的影响可以前后抵消掉，但是对于D项的影响是随机的并且影响非常大。所以如果取平均值可以减轻影响，但是取平均值又会产生一定延迟，所以我们采用2项的加权平均值来减轻斜率误差变向的问题。

不完全微分实现思路：给微分项加入一阶惯性单元（低通滤波器）

普通PID的微分项输出： dout(k)=K_d∗(error(k)−error(k−1))

不完全微分PID的微分项输出： dout(k)=(1−α)∗K_d∗(error(k)−error(k−1))+α∗dout(k−1)

即采用加权平均值使微分项输出更加平滑。

Actual += Encoder_Get();
Error1 = Error0;
Error0 = Target - Actual;
if(K_I != 0){ErrorInt += Error0;}
else{ErrorInt = 0;}
DOut = (1 - a) * K_D * (Error0 - Error1) + a * DOut;
Out = K_P * Error0 + K_I * ErrorInt + DOut;