当前位置： 首页 > news >正文

卷积层（Convolutional Layer）学习笔记

news 2025/10/9 5:52:13

卷积层是卷积神经网络（CNN）的核心组件，其设计灵感来源于人类视觉系统对局部特征的感知机制。它通过卷积操作从输入数据中提取特征，是处理图像、视频等网格结构数据的关键技术。

一、卷积层的核心原理

1. 什么是卷积操作？

卷积操作是通过卷积核（Kernel/Filter） 在输入数据上滑动，对每个局部区域进行元素相乘再求和的运算，最终生成特征图（Feature Map） 的过程。

直观理解：想象用一个放大镜（卷积核）观察一幅画（输入图像），每次移动放大镜（滑动），就会得到该区域的一个 "特征描述"（特征图上的一个点）。

3×3 卷积核处理 5×5 输入：

输入矩阵       卷积核        计算过程               输出特征图
[[1 2 3]       [[1 0 1]     1×1 + 2×0 + 3×1      [[(1+3),  (2+4)][4 5 6]   *    [0 1 0]  =  4×0 + 5×1 + 6×0  →   [(4+6),  (5+7)]][7 8 9]]       [1 0 1]     7×1 + 8×0 + 9×1

可视化卷积原理图

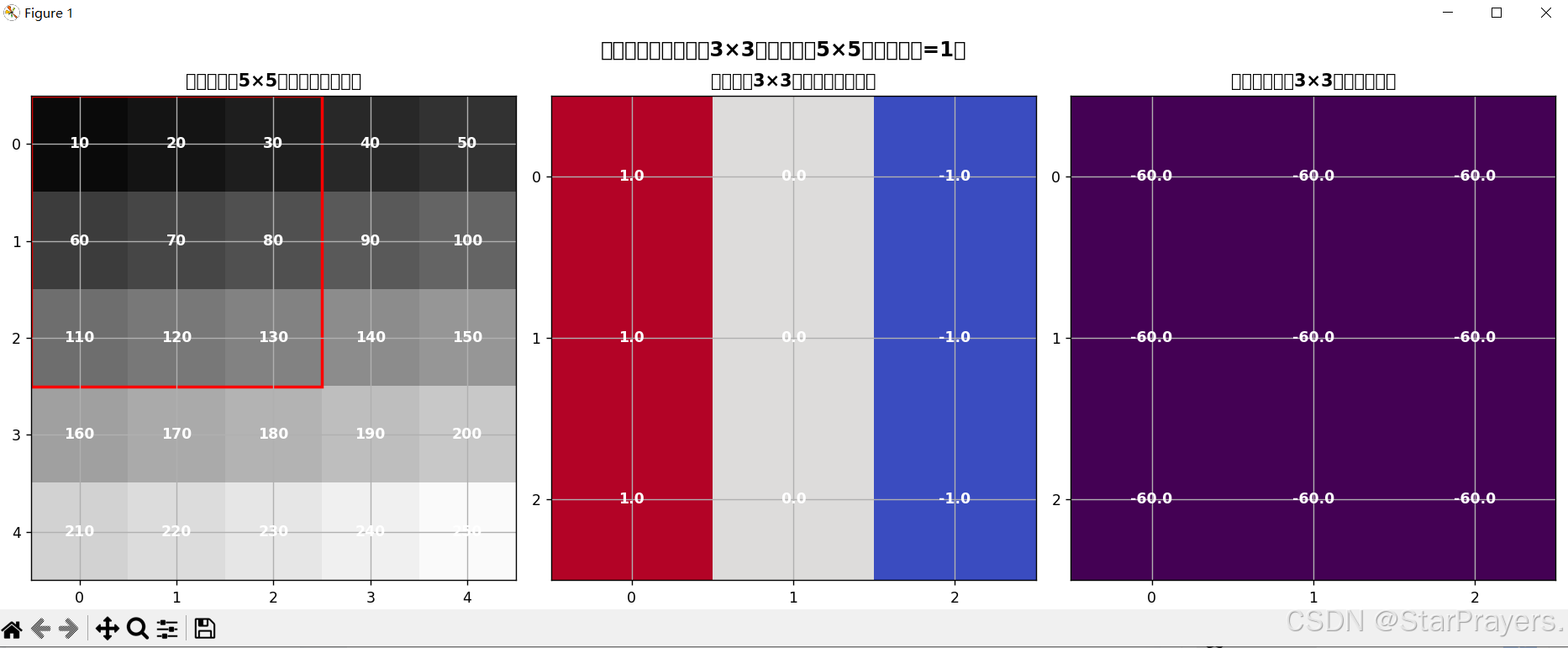
可视化卷积原理图代码放在文章末尾（复制到 Python 环境即可运行）

1.1. 3×3 卷积核（Kernel）

  • 含义：指卷积核是一个 3 行 3 列 的二维矩阵（正方形）。
  • 作用：作为 "特征探测器"，每次只关注输入数据中 3×3 大小的局部区域。
  • 示例：一个 3×3 的边缘检测卷积核：
  • [[1,  0, -1],[1,  0, -1],[1,  0, -1]]
    • 为什么是 3×3？这是深度学习中最常用的卷积核尺寸之一：太小（如 1×1）提取特征能力有限，太大（如 7×7）会增加计算量，而 3×3 既能捕捉局部特征，又能保持计算效率。

1.2. 5×5 输入（Input）

  • 含义：指输入数据是一个 5 行 5 列 的二维矩阵（可以是单通道图像的像素矩阵）。
  • 示例：一个 5×5 的灰度图像像素值矩阵：
[[1, 2, 3, 4, 5],[6, 7, 8, 9, 10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]

1.3. 两者的关系（可视化卷积过程）

当 3×3 卷积核处理 5×5 输入时，过程如下：

  1. 卷积核从输入的左上角开始，覆盖输入的 (1,1) 到 (3,3) 区域（左上角 3×3 区域）。
  2. 逐元素相乘后求和，得到输出特征图的第一个值。
  3. 卷积核按步长（如步长 = 1）向右 / 向下滑动，重复上述计算，直到遍历整个 5×5 输入。

最终输出尺寸（假设步长 = 1，无填充）：输入 5×5 → 卷积核 3×3 → 输出 3×3（计算公式：(5-3)/1 + 1 = 3）。

通过这个过程，大尺寸的输入数据被 "压缩" 为更小的特征图，同时保留了关键的局部特征。

2. 卷积核（Kernel）

  • 定义：一个小型的多维数组（图像处理中通常是 2D 矩阵）
  • 作用：充当 "特征探测器"，不同的卷积核可以提取不同特征（如边缘、纹理、颜色等）
  • 示例：
    • 垂直边缘检测核：[[1, 0, -1], [1, 0, -1], [1, 0, -1]]
    • 水平边缘检测核：[[1, 1, 1], [0, 0, 0], [-1, -1, -1]]

3. 滑动与步长（Stride）

  • 滑动方式：卷积核从输入的左上角开始，从左到右、从上到下滑动
  • 步长：每次滑动的像素数（默认为 1）
    • 步长 = 1：相邻两次滑动重叠区域大
    • 步长 = 2：滑动幅度大，输出特征图尺寸更小
步长=1时的滑动路径：→→→ （每次移动1格）
步长=2时的滑动路径：→→→ （每次移动2格，间隔更大）

4. 填充（Padding）

  • 定义：在输入数据的边缘添加 0 值像素
  • 作用：控制输出特征图的尺寸，避免边缘信息丢失
  • 常见模式：
    • padding=0：无填充（输出尺寸缩小）
    • padding=1：在边缘添加 1 圈 0（3×3 卷积核可保持尺寸不变）

尺寸计算公式：若输入尺寸为H×W，卷积核大小K×K，步长S，填充P，则输出尺寸为：

输出高度 = (H - K + 2P) / S + 1
输出宽度 = (W - K + 2P) / S + 1

5.卷积的三种模式：full, same, valid

参考卷积的三种模式：full, same, valid_陌上小布的博客-CSDN博客_卷积神经网络valid

二、卷积层的工作流程

以处理 CIFAR10 图像（3 通道，32×32 像素）为例，完整流程如下：

  1. 输入数据：形状为(3, 32, 32)（通道数 × 高度 × 宽度）
  2. 卷积核准备：假设有 16 个 3×3 的卷积核，每个核形状为(3, 3, 3)（输入通道 × 核高 × 核宽）
  3. 卷积运算：
    • 每个卷积核与输入的 3 个通道分别卷积，再将结果相加
    • 16 个卷积核生成 16 个特征图
  4. 输出特征图：形状为(16, 32, 32)（输出通道数 × 高度 × 宽度）
输入 (3,32,32) → [16个(3,3,3)卷积核] → 输出 (16,32,32)（RGB图像）   （提取16种不同特征）   （16个特征图）

想更直观理解可参考卷积神经网络之卷积层理解(持续更新)-CSDN博客

三、卷积层的关键优势

  1. 局部连接：每个神经元只关注输入的局部区域（符合视觉系统特性）

    • 例如：3×3 卷积核只关注 3×3 的局部区域

  2. 权值共享：同一卷积核在整个输入上共享权重

    • 优势：大幅减少参数数量
    • 对比：32×32 图像用全连接层需要 1024 个参数，而 3×3 卷积核仅需 9 个参数

  3. 平移不变性：目标在图像中位置变化时仍能被识别

    • 例如：无论猫在图像左侧还是右侧，边缘检测核都能识别其轮廓

四、卷积层在 PyTorch 中的实现

nn.Conv2d是 PyTorch 中 2D 卷积层的实现，关键参数如下：

import torch.nn as nn# 定义一个卷积层
conv = nn.Conv2d(in_channels=3,      # 输入通道数（RGB图像为3）out_channels=16,    # 卷积核数量（输出通道数）kernel_size=3,      # 卷积核大小（3×3）stride=1,           # 步长padding=1           # 填充（保持尺寸不变）
)# 输入：批次大小=64，3通道，32×32图像
input_tensor = torch.randn(64, 3, 32, 32)
output_tensor = conv(input_tensor)
print(output_tensor.shape)  # 输出：torch.Size([64, 16, 32, 32])

五、卷积层的扩展应用

  1. 不同维度的卷积：

    • 1D 卷积：处理序列数据（文本、音频）
    • 3D 卷积：处理视频数据（加入时间维度）

  2. 特殊卷积类型：

    • 转置卷积（Transposed Convolution）：

      • 作用：上采样（增大特征图尺寸）
      • 应用：图像分割、生成对抗网络（GAN）

    • 深度可分离卷积（Depthwise Separable Convolution）：

      • 原理：将标准卷积拆分为 "深度卷积" 和 "逐点卷积"
      • 优势：减少计算量和参数数量（MobileNet 等轻量网络核心）

    • 空洞卷积（Dilated Convolution）：

      • 特点：卷积核中加入 "空洞"（空格），增大感受野
      • 应用：语义分割（无需下采样即可获得大视野）

  3. 实际应用场景：

    • 图像分类（ResNet、EfficientNet）
    • 目标检测（YOLO、Faster R-CNN）
    • 图像生成（StyleGAN、Stable Diffusion）
    • 医学影像分析（肿瘤检测）

六、可视化理解卷积层效果

通过可视化不同层的特征图，可以直观理解卷积层的工作：

  1. 浅层卷积层：提取边缘、纹理、颜色等低级特征

    • 示例：垂直边缘、水平边缘、斑点等

  2. 深层卷积层：提取更复杂的高级特征

    • 示例：眼睛、车轮、纹理组合等
输入图像 → 第1层特征图（边缘） → 第2层特征图（局部形状） → 第3层特征图（物体部件）

七、总结

卷积层通过卷积核的滑动计算，实现了对输入数据的局部特征提取，凭借局部连接、权值共享等特性，在保持强大特征提取能力的同时大幅减少了参数数量。从简单的边缘检测到复杂的图像生成，卷积层已成为计算机视觉领域不可或缺的核心技术，也是理解更复杂神经网络（如 Transformer 与 CNN 结合模型）的基础。

可视化卷积原理图代码（复制到 Python 环境即可运行）

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches# ---------------------- 1. 定义卷积相关参数 ----------------------
# 输入：5×5的模拟灰度图像（像素值0-255）
input_matrix = np.array([[10, 20, 30, 40, 50],[60, 70, 80, 90, 100],[110, 120, 130, 140, 150],[160, 170, 180, 190, 200],[210, 220, 230, 240, 250]
], dtype=np.float32)# 卷积核：3×3的边缘检测核（垂直边缘）
kernel = np.array([[1, 0, -1],[1, 0, -1],[1, 0, -1]
], dtype=np.float32)stride = 1  # 步长
padding = 0  # 无填充# 计算输出特征图尺寸
in_h, in_w = input_matrix.shape
kernel_h, kernel_w = kernel.shape
out_h = (in_h - kernel_h + 2 * padding) // stride + 1
out_w = (in_w - kernel_w + 2 * padding) // stride + 1
output_matrix = np.zeros((out_h, out_w), dtype=np.float32)  # 初始化输出# ---------------------- 2. 计算卷积结果（核心过程） ----------------------
for i in range(out_h):for j in range(out_w):# 确定当前卷积核在输入上的位置（滑动窗口）h_start = i * strideh_end = h_start + kernel_hw_start = j * stridew_end = w_start + kernel_w# 局部区域提取 + 元素相乘 + 求和（卷积核心运算）local_region = input_matrix[h_start:h_end, w_start:w_end]output_matrix[i, j] = np.sum(local_region * kernel)# ---------------------- 3. 绘制可视化图 ----------------------
fig, axes = plt.subplots(1, 3, figsize=(15, 5))  # 1行3列布局：输入、卷积核、输出
fig.suptitle('卷积层原理可视化（3×3卷积核处理5×5输入，步长=1）', fontsize=14, fontweight='bold')# 子图1：输入矩阵（5×5）
ax1 = axes[0]
ax1.imshow(input_matrix, cmap='gray', vmin=0, vmax=255)
ax1.set_title('输入矩阵（5×5，模拟灰度图像）', fontweight='bold')
# 标注像素值
for i in range(in_h):for j in range(in_w):ax1.text(j, i, int(input_matrix[i, j]), ha='center', va='center', color='white', fontweight='bold')
# 绘制初始滑动窗口（3×3红色边框）
rect = patches.Rectangle((-0.5, -0.5), kernel_w, kernel_h, linewidth=2, edgecolor='red', facecolor='none')
ax1.add_patch(rect)
ax1.set_xticks(range(in_w))
ax1.set_yticks(range(in_h))
ax1.grid(True)# 子图2：卷积核（3×3）
ax2 = axes[1]
ax2.imshow(kernel, cmap='coolwarm', vmin=-1, vmax=1)
ax2.set_title('卷积核（3×3，垂直边缘检测）', fontweight='bold')
# 标注卷积核数值
for i in range(kernel_h):for j in range(kernel_w):ax2.text(j, i, kernel[i, j], ha='center', va='center', color='white', fontweight='bold')
ax2.set_xticks(range(kernel_w))
ax2.set_yticks(range(kernel_h))
ax2.grid(True)# 子图3：输出特征图（3×3）
ax3 = axes[2]
ax3.imshow(output_matrix, cmap='viridis')
ax3.set_title('输出特征图（3×3，边缘特征）', fontweight='bold')
# 标注输出值（保留1位小数）
for i in range(out_h):for j in range(out_w):ax3.text(j, i, f'{output_matrix[i, j]:.1f}', ha='center', va='center', color='white', fontweight='bold')
ax3.set_xticks(range(out_w))
ax3.set_yticks(range(out_h))
ax3.grid(True)plt.tight_layout()
plt.savefig('卷积层原理可视化.png', dpi=300, bbox_inches='tight')  # 保存图片（300分辨率，清晰）
plt.show()
http://www.dtcms.com/a/456915.html

相关文章：

  • centos7.6系统python3安装IOPaint (原Lama-Cleaner)
  • Shell脚本基础应用
  • 107、23种设计模式之观察者模式（16/23）
  • Linux进程第五讲：PPID与bash的关联、fork系统调用的原理与实践操作（上）
  • 精品购物网站如何创建个人主页
  • 怎样建设电子商务网站wordpress 4.9 中文
  • AI赋能锂电：机器学习加速电池技术革新
  • await
  • 机器学习-常用库
  • 前端网络与优化
  • (二) 机器学习之卷积神经网络
  • GAN入门：生成器与判别器原理（附Python代码）
  • 企业网站seo报价校园门户网站开发需求
  • RabbitMQ核心机制
  • 四、代码风格规范
  • 做网站采集青岛做教育的网站建设
  • Ethernaut Level 8: Vault - 私有变量读取
  • 去水印擦除大师 3.7.6 | 专门用于去除视频和图片水印的工具，支持多个热门平台无水印下载
  • 关键词排名优化网站东营交通信息网官网
  • 【URP】Unity[内置Shader]复杂光照ComplexLit
  • 【Linux】vim的操作大全
  • Web Worker：释放前端性能的“后台线程”技术
  • 机械行业网站建设方案电商公司有哪些?
  • 赋能智能制造领域：全星QMS质量管理软件系统深度解析
  • java返回参数报错
  • cesium126，230217，Pixel Streaming in Unreal Engine 像素流 - 1 基本概念：
  • JavaScript基础知识
  • 以太网数据报文各协议字段深度解析（第一、二章）
  • microsoft做网站浙江建设培训中心网站
  • 从LLM角度学习和了解MoE架构