单链表的应用02---算法中的暴力美学(第八讲)

算法题六. 相交链表

题目来源：https://leetcode.cn/problems/intersection-of-two-linked-lists/description/

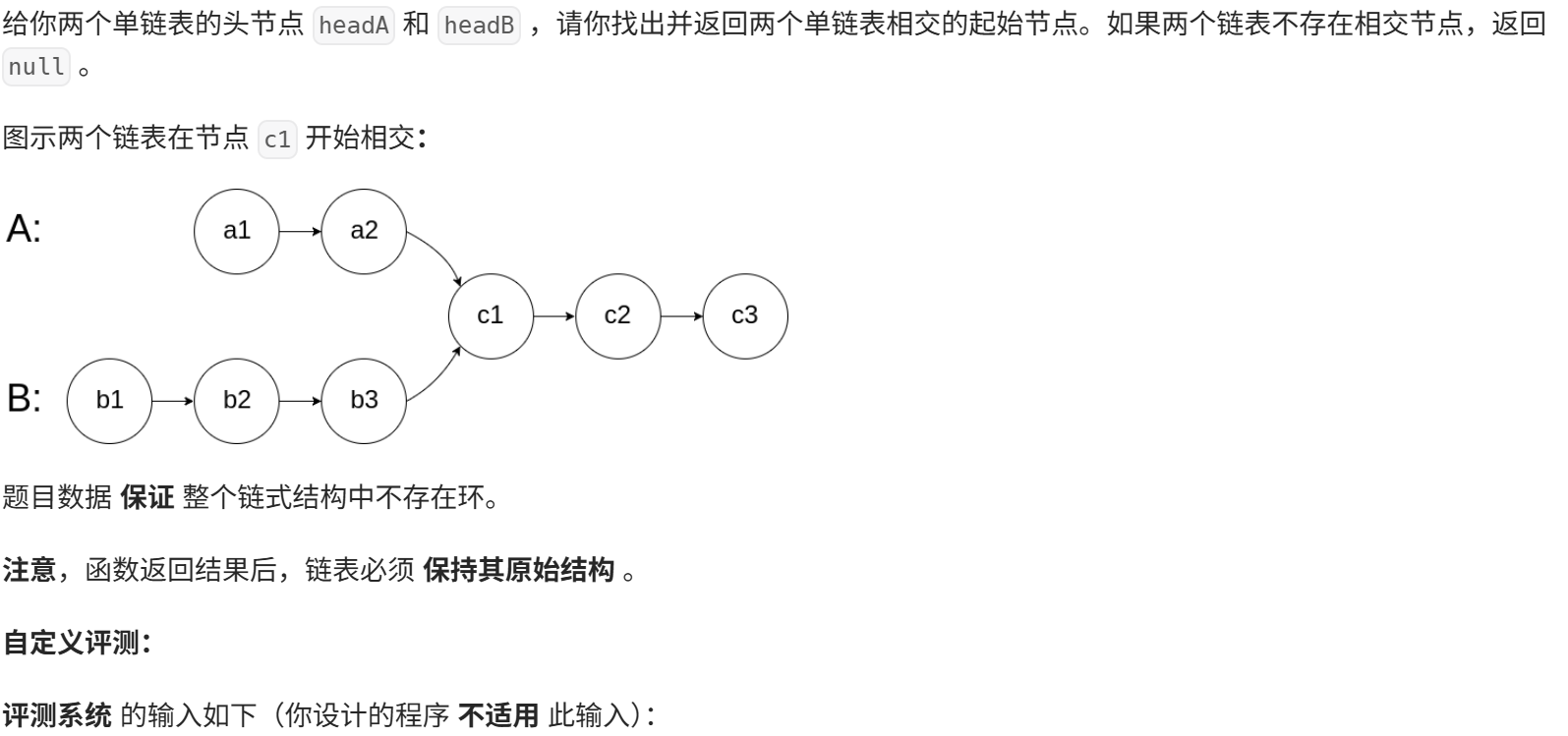
由分析可知：相交链表也就以下这三种情况：

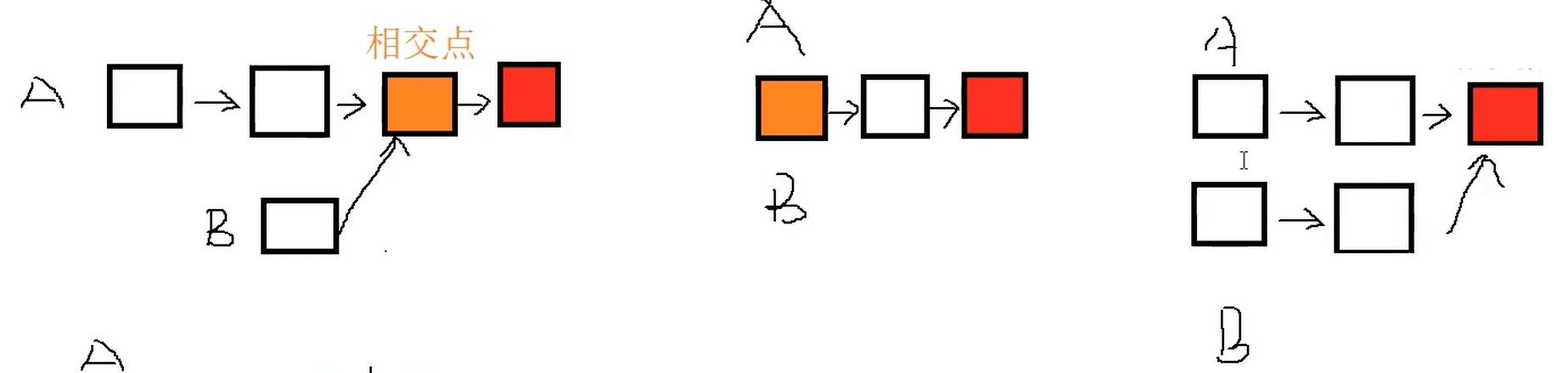
   注意：下面这种“八叉型”的相交在链表中不存在这种结构，因为相交点的next指针不可能同时指向两个节点。

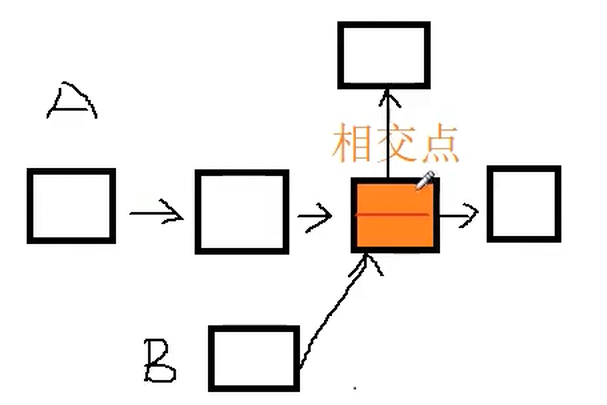
   则我们可以得出如下结论：两个链表的尾结点相同，则两个链表一定相交。

   思路：求两个链表的长度，长的那个链表先走“两个链表长度差”步，走完后，长短链表开始同步遍历，找相同的节点。

typedef struct ListNode ListNode;ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {//1.求两个链表长度 ListNode* pa=headA;ListNode* pb=headB;int sizeA=0,sizeB=0;while(pa){++sizeA;pa=pa->next;}while(pb){++sizeB;pb=pb->next;}//2.求两个链表长度差int gap=abs(sizeA-sizeB);//3.看哪个链表长，哪个就先走长度差ListNode* shortlist=headA;ListNode* longlist=headB;if(sizeA>sizeB){shortlist=headB;longlist=headA;}//4.让长链表先走gapwhile(gap--){longlist=longlist->next;}//5.longlist,shortlist在同一起跑线,开始遍历比较while(shortlist)//等价于“while(longlist)”{if(shortlist==longlist){return shortlist;}shortlist=shortlist->next;longlist=longlist->next;}//链表不相交return NULL;}

---

算法题七. 环形链表I

题目来源：https://leetcode.cn/problems/linked-list-cycle/description/

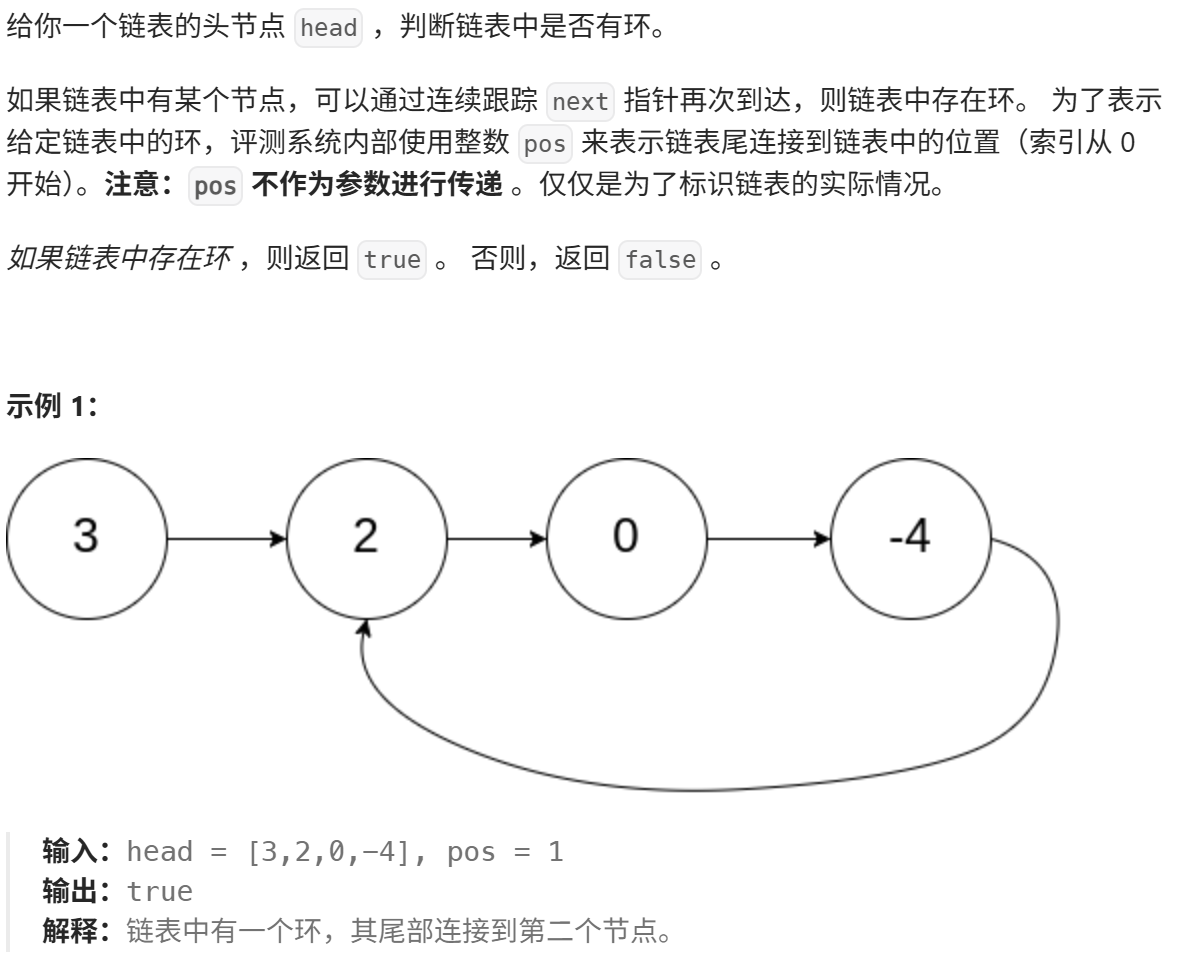
   思路：快慢指针，慢指针每次走一步，快指针每次走两步，如果slow指针和fast指针指向同一个节点，说明链表带环。

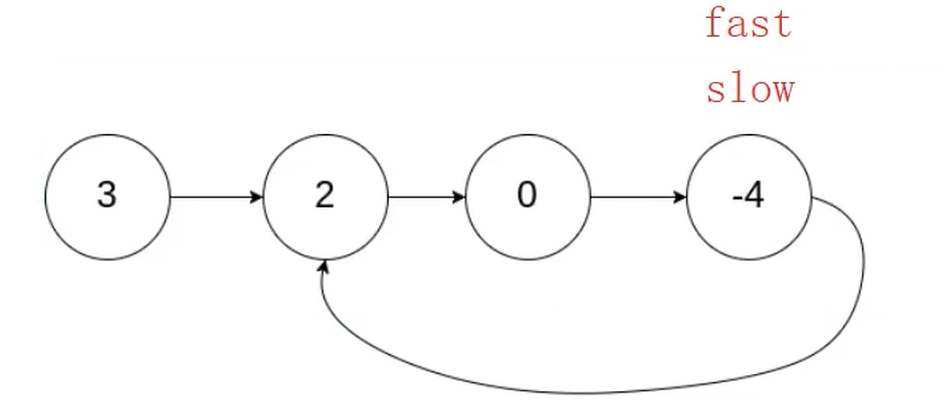
typedef struct ListNode ListNode;bool hasCycle(ListNode *head) {//创建快慢指针ListNode* slow=head;ListNode* fast=head;while(fast!=NULL&&fast->next!=NULL){slow=slow->next;fast=fast->next->next;if(fast==slow){//快慢指针相遇return true;}}//链表不带环return false;}

       疑问一：但是老铁们，话说回来，你怎么就知道这道题慢指针走一步，快指针就走两步就能相遇呢？难道就不存在不会相遇的情况呢？

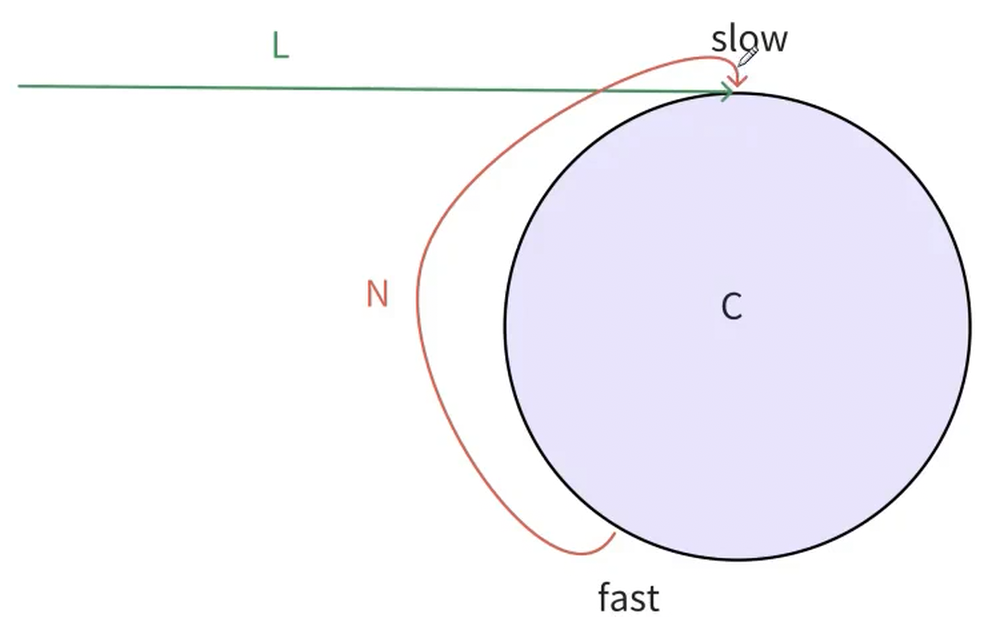
       具体过程抽象如上图，显而易见，fast指针走得快，fast指针一定会比slow指针先入环，假设此时slow指针刚入环，设slow和fast之间的最大距离为N，此时此刻，slow和fast指针都在环里，这时候就变成了一个追击相遇问题(fast会追slow)，fast每走两步，slow就会走一步，它们之间的距离就变成N-1；此时再次fast每走两步，slow走一步，它们之间的距离就变成N-2；依次递推，随着时间推移，slow和fast的距离会逐渐缩小，直至最后相遇：N-3,N-4,.......2，1,0。

      疑问二：由疑问一的证明可知，在环中，快指针走两步，慢指针走一步，两个指针一定会相遇，那快指针走三步或者四步或者五步...，那快慢指针会不会相遇呢？

       假设此时slow指针刚入环，设slow和fast之间的最大距离为N，慢指针每次走一步，快指针每次走三步，则二者之间的距离缩短至N+1-3=N-2,依次递推，距离缩短至N-2+1-3=N-4,N-6,...4,2,0但是这种情况相遇，N必须为偶数，如果N为奇数，那距离就会变成...3,1,-1，（-1表示fast此时已经跑到slow前面了,变成slow追fast，随着时间推移，二者之间距离会越来越大），往后会发生套圈现象，设圈周长为C,则此时距离为C-1（这一圈没追上），那下一圈是否会追上？N为奇数，下一圈开始追逐，若C-1为奇数，即C为偶数，一定不会相遇；若C-1为偶数，即C为奇数，一定会相遇，此种情况不成立。

     疑问三：此时C-1到底是奇数还是偶数？

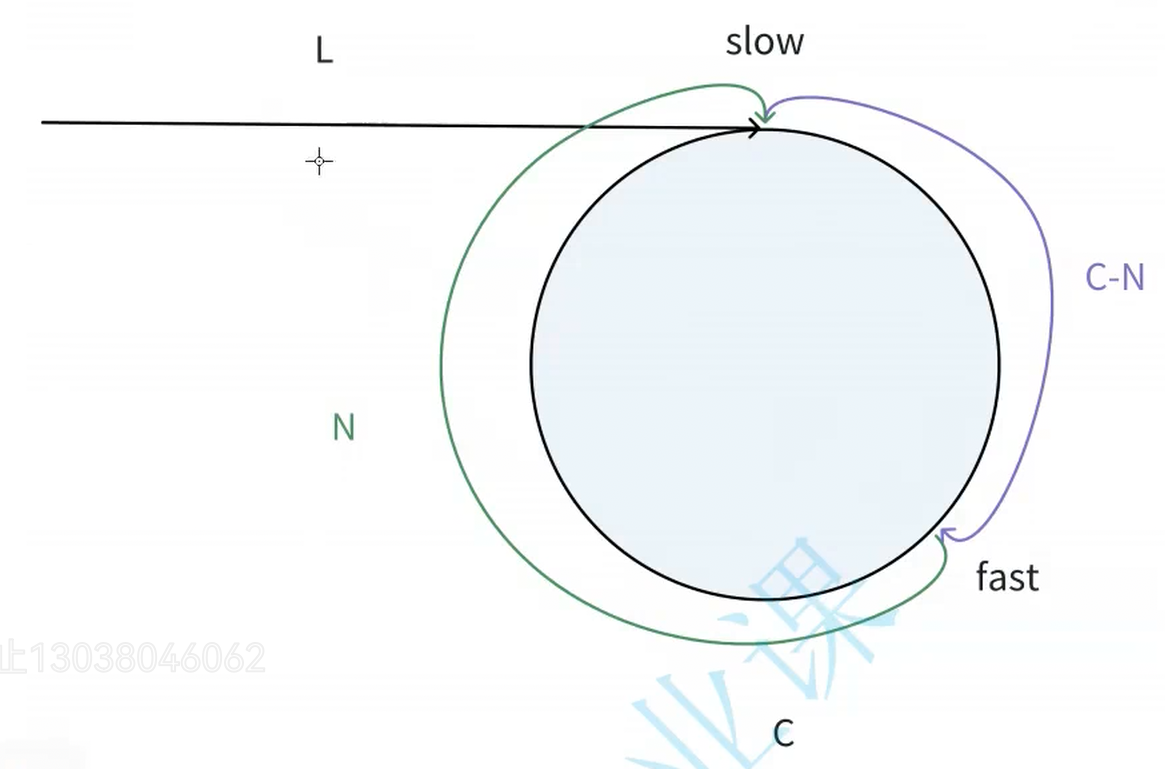
       慢指针每次走一步，快指针每次走三步，快慢指针之间的路程关系为：3*慢指针=快指针。如上图所示，假如说slow指针在入环节点的位置，则慢指针走的总路程为L,快指针走的总路程为L+C-N，但是也有可能fast已经绕了好几圈到那个位置slow才入环。则此时快指针的路程为L+C-N+nC。将其代入蓝色公式中最终可得：2L=(n+1)C-N。最终结论：N为奇数，C为奇数，一定会相遇。

       综上，对于疑问二，我们的回答是肯定的。

---

算法题八. 环形链表II       

题目来源：https://leetcode.cn/problems/linked-list-cycle-ii/description/

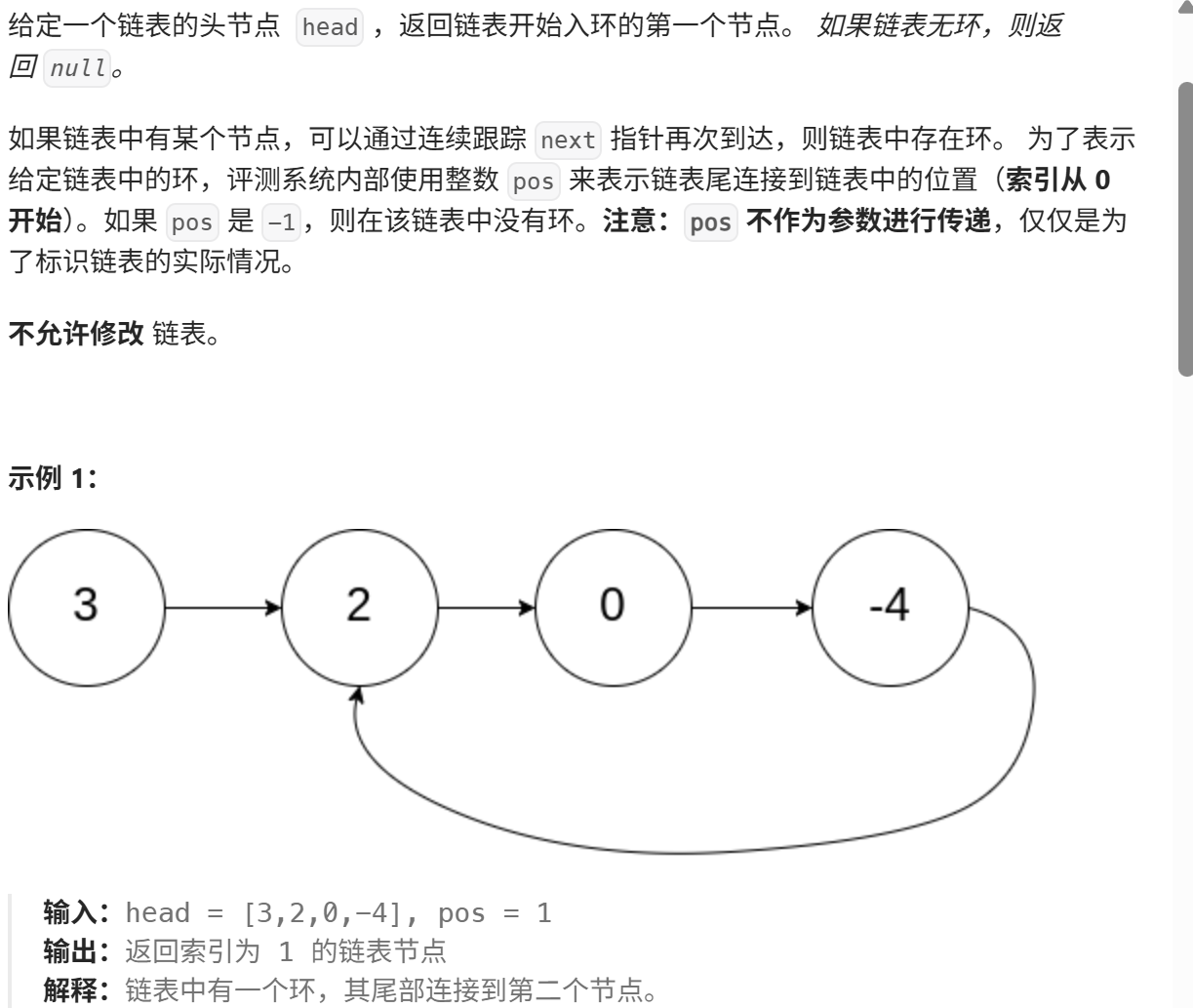
思路：快慢指针，在环里一定会相遇，相遇点到入环节点的距离=头节点到入环节点的距离。

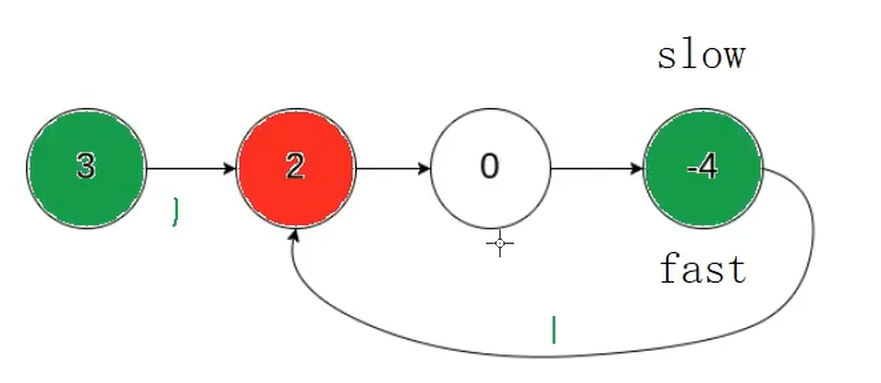
typedef struct ListNode ListNode;ListNode *detectCycle(ListNode *head) {ListNode* slow=head;ListNode* fast=head;while(fast!=NULL&&fast->next!=NULL){slow=slow->next;fast=fast->next->next;if(fast==slow){//相遇点--找入环节点ListNode* pcur=head;while(pcur!=slow){pcur=pcur->next;slow=slow->next;}return pcur;  //也可返回slow}}//链表不带环return NULL;}

  证明：为什么在带环链表中，快慢指针相遇点到入环节点的距离=头节点到入环节点的距离？

  

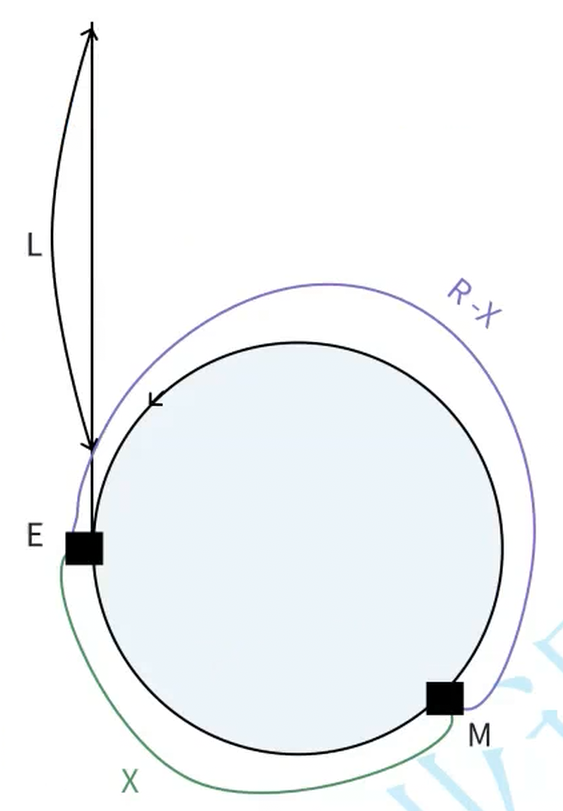
        如上图：E代表入环节点，M代表相遇节点，假设环的周长为R,头节点到入环节点的距离为L,慢指针再相遇点走的路程：L+X,快指针在相遇点走的路程L+X+nR,由于slow*2=fast，则可得出：L=(n-1)R+R-X。可知（n-1）R与快慢指针相遇无关，所以可以不计，则最终L=R-X,所以结论成立，得证！

---

       以上就是今天的内容，下节我将讲述难度更大一些的关于单链表的算法题，链表分割和随机链表的复制。感兴趣的朋友们可以一键三连喔~