LeetCode 分类刷题：1901. 寻找峰值 II

题目

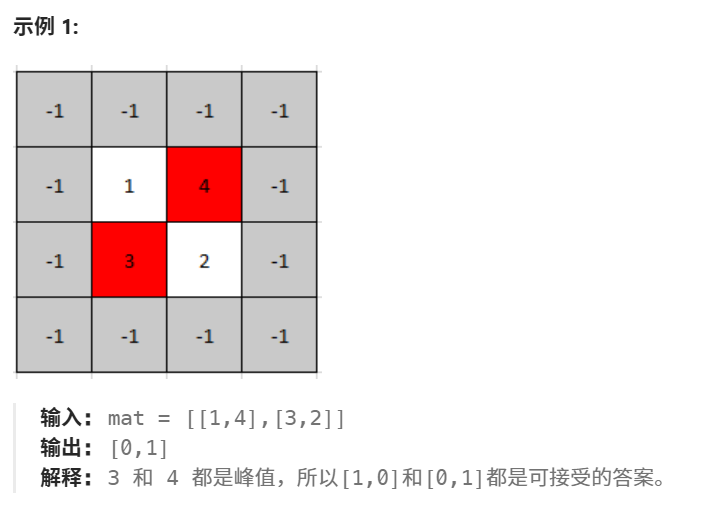
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。

给你一个 从 0 开始编号 的 m x n 矩阵 mat ，其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。

你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。

要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法

解析

利用行最大值判断峰顶位置

我们可以二分包含峰顶的行号 i：

• 如果 mat[i] 的最大值比它下面的相邻数字小，则存在一个峰顶，其行号大于 i。缩小二分范围，更新二分区间左端点 left。
• 如果 mat[i] 的最大值比它下面的相邻数字大，则存在一个峰顶，其行号小于或等于 i。缩小二分范围，更新二分区间右端点 right。

对于本题，如果每次二分，都是 mat[i] 的最大值比它下面的相邻数字小，那么最后会判断出峰顶行号大于 m−2，此时可以直接确定最后一行必然包含峰顶。

这意味着 m−1 不需要在初始二分范围内，初始二分范围为 [0,m−2]。在这个范围中二分，如果每次都更新的是区间左端点 left，那么最后得到的二分结果必然是 m−1。

如果在 [0,m−1] 中二分，还需要额外判断 i+1 是否越界。在 [0,m−2] 中二分可以避免越界判断。

作者：灵茶山艾府
链接：https://leetcode.cn/problems/find-a-peak-element-ii/solutions/2571587/tu-jie-li-yong-xing-zui-da-zhi-pan-duan-r4e0n/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

答案

class Solution:def findPeakGrid(self, mat: List[List[int]]) -> List[int]:left, right = -1, len(mat) - 1while left + 1 < right:i = (left + right) // 2mx = max(mat[i])if mx > mat[i + 1][mat[i].index(mx)]:right = i  # 峰顶行号 <= ielse:left = i  # 峰顶行号 > ireturn [right, mat[right].index(max(mat[right]))]# 作者：灵茶山艾府
# 链接：https://leetcode.cn/problems/find-a-peak-element-ii/solutions/2571587/tu-jie-li-yong-xing-zui-da-zhi-pan-duan-r4e0n/
# 来源：力扣（LeetCode）
# 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析

时间复杂度：O(nlogm)，其中 m 和 n 分别为 mat 的行数和列数。需要二分 O(logm) 次，每次二分需要 O(n) 的时间寻找 mat[i] 最大值的下标。
空间复杂度：O(1)。仅用到若干额外变量。

作者：灵茶山艾府
链接：https://leetcode.cn/problems/find-a-peak-element-ii/solutions/2571587/tu-jie-li-yong-xing-zui-da-zhi-pan-duan-r4e0n/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。