当前位置：首页 > news >正文

力扣每日一题（一）双指针 + 状态转移dp 矩阵快速幂

news 2025/10/6 6:26:38

1. 雨水三件套 -- 双指针移动

1. 盛最多水的容器

2. 接雨水

3. 接雨水二维版本

1498. 满足条件的子序列数目

2. 状态转移 dp + 矩阵快速幂

1931. 用三种不同颜色为网格涂色

790. 多米诺和托米诺平铺

3337. 字符串转换后的长度 II

1. 雨水三件套 -- 双指针移动

https://www.bilibili.com/video/BV1Qg411q7ia/?vd_source=de9fa87d5ebe1c5acf589d3c19333957

1. 盛最多水的容器

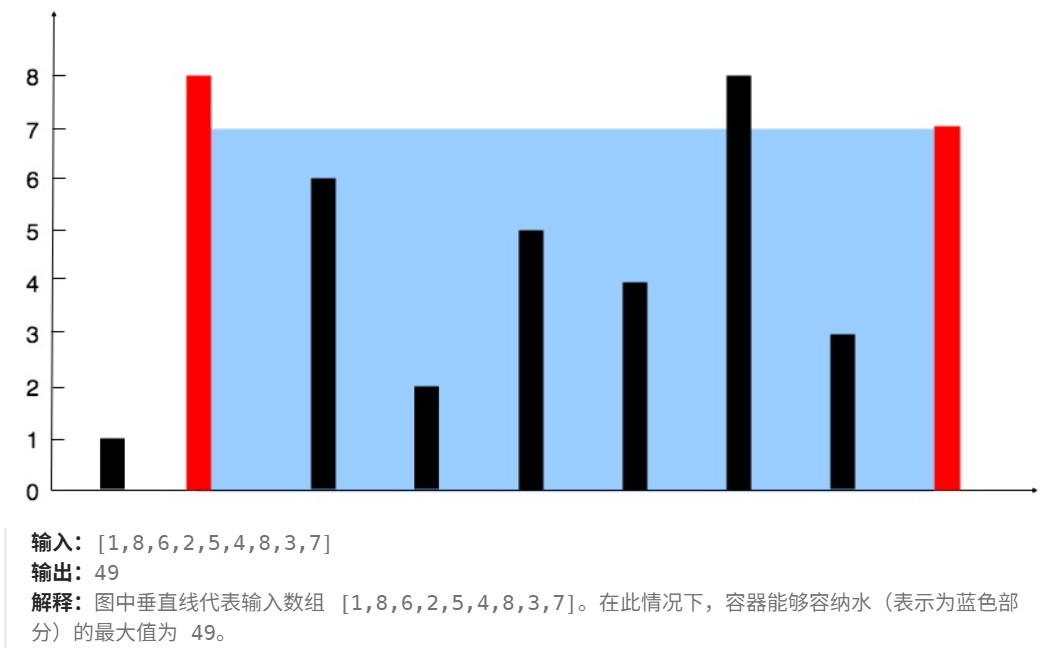
选两根柱子作为容器（宽度为距离高度为更短的那根）

双指针移动：每次移动短的那根（因为场上已经不可能以短边为答案了）

（因为高度上现在高度就是短边高度，容器高度都≤短边高度；再往里面缩 宽度也变小）

class Solution:def maxArea(self, height: List[int]) -> int:ans, l, r = 0, 0, len(height)-1while l < r:ans = max(ans, min(height[l], height[r])*(r-l))# 移动if height[l] < height[r]:l += 1else:r -= 1return ans

2. 接雨水

黑为柱子高度蓝为雨水量。每个位置能接的是 左右两侧最大位置 较小的那个。（不然会向那个方向溢出）

思路一：先算一下后缀最大，再从左边一边算前缀最大，一边统计答案。

class Solution:def trap(self, height: List[int]) -> int:n, ans, maxn = len(height), 0, height[0]hou = [0] * nhou[-1] = height[-1] # 后缀for i in range(n-2,-1,-1):hou[i] = max(hou[i+1], height[i])for i in range(1,n):maxn = max(maxn, height[i]) # 前缀ans += min(maxn, hou[i]) - height[i]            return ans

思路二：类似上一题也从左右向中间双指针移动

假设红色是我们已经知道的信息，现在第二个位置左边最大值已经知道为1；

但中间绿色的我们还没遍历到，右边现在最大值是3，即右侧最大值至少是3。

所以左右最大值的 较小值就可以知道是1 统计并把左指针移动。（移动短的那个）

class Solution:def trap(self, height: List[int]) -> int:ans, l, r = 0, 0, len(height)-1while l < r:if height[l] < height[r]: # 移动短的那个if height[l+1] < height[l]:ans += height[l] - height[l+1]height[l+1] = height[l] # 更新前缀最大值l+=1else:if height[r-1] < height[r]:ans += height[r] - height[r-1]height[r-1] = height[r]r-=1return ans

3. 接雨水二维版本

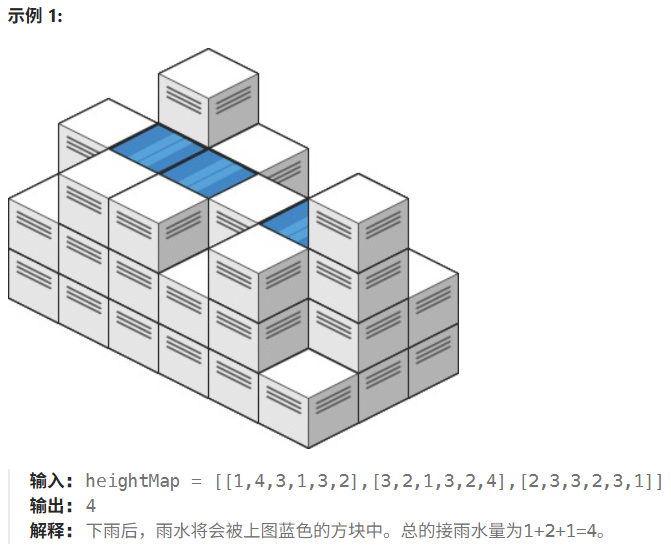
和一维的思路一样我们从外而内看：最外一圈是接不了水的，（维护一下“最外一圈”）

从现在最外一圈找最短的那个木板，它的临近位置能达到的水位线 就是当前集合最短木板的高度。

统计+进堆（相当于往里面缩圈）并且移除最短木板。

由于每次要找最短的木板，使用堆 heap 来维护。

class Solution:def trapRainWater(self, Map: List[List[int]]) -> int:n, m, h, ans = len(Map), len(Map[0]), [], 0# 存最外面一圈 建立堆for i, row in enumerate(Map):for j, hi in enumerate(row):if i==0 or i==n-1 or j==0 or j==m-1:h.append((hi, i, j))row[j] = -1heapify(h)while h:minn, i, j = heappop(h) # 最小出堆# 四个方向进 + 统计柱子for x, y in (i, j-1), (i, j+1), (i-1, j), (i+1, j):if 0 <= x < n and 0 <= y < m and Map[x][y] >= 0:ans += max(0, minn - Map[x][y])heappush(h, (max(minn, Map[x][y]), x, y))Map[x][y] = -1 # 进堆过 标为-1return ans

1498. 满足条件的子序列数目

统计并返回 nums 中能满足其最小元素与最大元素的和 小于或等于 target 的非空子序列的数目。

先选最小元素和最大元素分别是谁，中间的N个元素可以随便，即2^N种（先预处理存一下）

排序后，最小和最大分别为左右指针，

若没超过，就统计并右移左指针；超过太大了，就左移右指针。

MOD = 1_000_000_007
MX = 100_000pow2 = [1] * MX  # pow2[i] = 2 ** i % MOD
for i in range(1, MX):pow2[i] = pow2[i - 1] * 2 % MODclass Solution:def numSubseq(self, nums: List[int], target: int) -> int:nums.sort()ans = 0left, right = 0, len(nums) - 1while left <= right:  # 可以相等，此时子序列的最小最大是同一个数if nums[left] + nums[right] <= target:ans += pow2[right - left]left += 1else:right -= 1return ans % MOD

2. 状态转移 dp + 矩阵快速幂

1931. 用三种不同颜色为网格涂色

m*n 格子 三种颜色填充，相邻不同色的情况数。

数据范围 m<=5，先处理单独一列的情况数。从前一列到下一列，存一个状态转移矩阵（可以就是1）。

最终结果即对 f0 进行 n-1 次乘以状态转移矩阵。

import numpy as npMOD = 1_000_000_007# a^n @ f0 矩阵快速幂
def pow(a: np.ndarray, n: int, f0: np.ndarray) -> np.ndarray:res = f0while n:if n & 1:res = a @ res % MODa = a @ a % MODn >>= 1return resclass Solution:def colorTheGrid(self, m: int, n: int) -> int:pow3 = [3 ** i for i in range(m)] # 预处理 3^nvalid = [] # 单独一列合法for color in range(3 ** m):for i in range(1, m):if color // pow3[i] % 3 == color // pow3[i - 1] % 3:  # 相邻颜色相同breakelse:  # 没有中途 break，合法valid.append(color)nv = len(valid)m = np.zeros((nv, nv), dtype=object) # 转换合法for i, color1 in enumerate(valid):for j, color2 in enumerate(valid):for p3 in pow3:if color1 // p3 % 3 == color2 // p3 % 3:  # 相邻颜色相同breakelse:  # 没有中途 break，合法m[i, j] = 1f0 = np.ones((nv,), dtype=object)res = pow(m, n - 1, f0) # 也可以用幂库 res = np.linalg.matrix_power(m, n - 1) @ f0return np.sum(res) % MOD

790. 多米诺和托米诺平铺

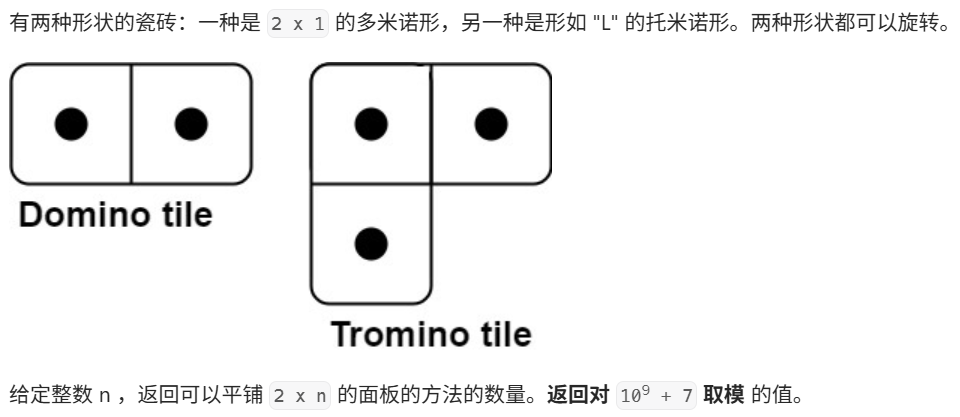
法一：把竖过来两个格子作为4种情况

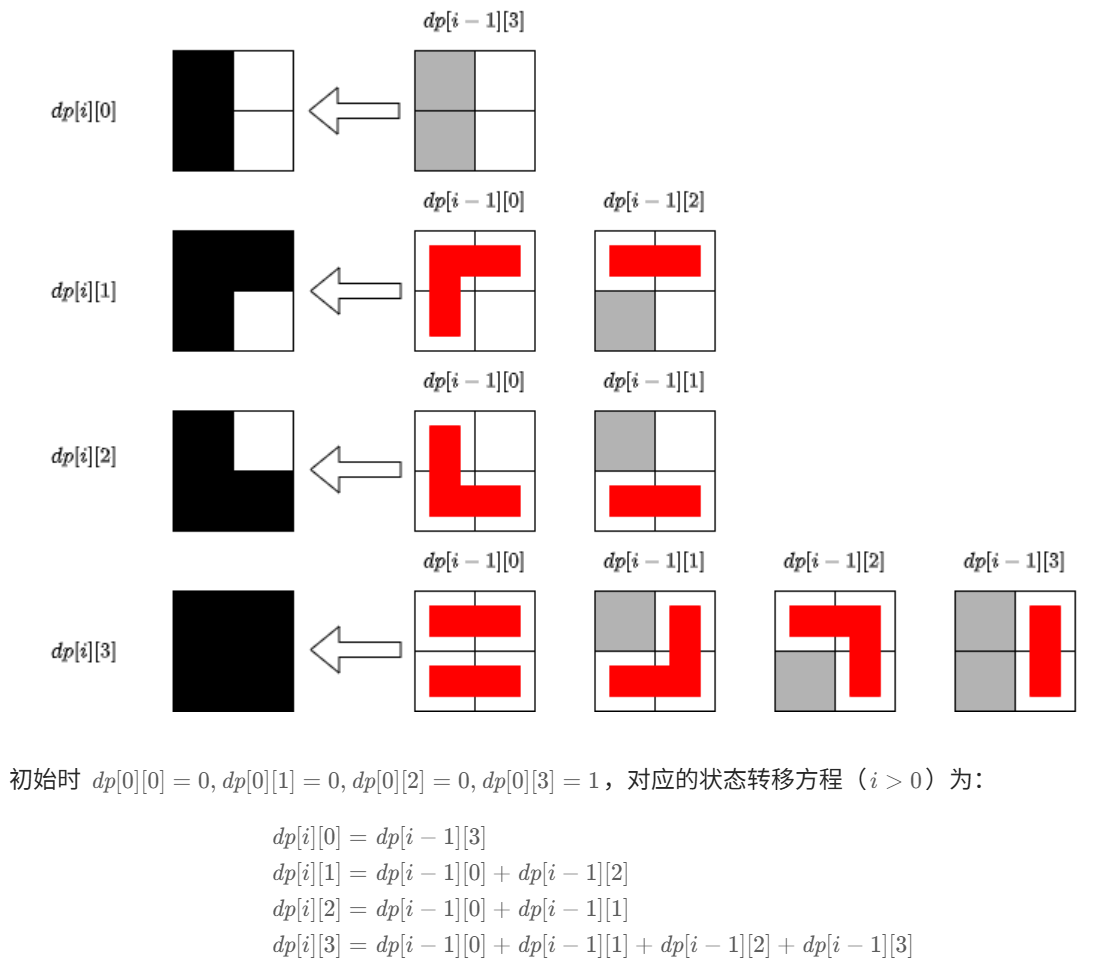
class Solution:def numTilings(self, n: int) -> int:MOD = 10 ** 9 + 7dp = [[0] * 4 for _ in range(n + 1)]dp[0][3] = 1for i in range(1, n + 1):dp[i][0] = dp[i - 1][3]dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MODdp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % MODdp[i][3] = (((dp[i - 1][0] + dp[i - 1][1]) % MOD + dp[i - 1][2]) % MOD + dp[i - 1][3]) % MODreturn dp[n][3]

快速幂写法

import numpy as npMOD = 10**9 + 7class Solution:def numTilings(self, n: int) -> int:# 构建转移矩阵 M: 4x4M = np.array([[0, 0, 0, 1],[1, 0, 1, 0],[1, 1, 0, 0],[1, 1, 1, 1]], dtype=object)init = np.array([0, 0, 0, 1], dtype=object)# 计算 M^n * initM_power = np.linalg.matrix_power(M, n)result = M_power @ initreturn result[3] % MOD

法二：根据前几项递推得

最后竖着放 1 最后横着放 2 ；就是 f[i-1] + f[i-2]。

最后放正L 负L 两种情况对应其他。2 sigma 前面的

最终递推方程 a^n = 2 a^n-1 + a^n-3。

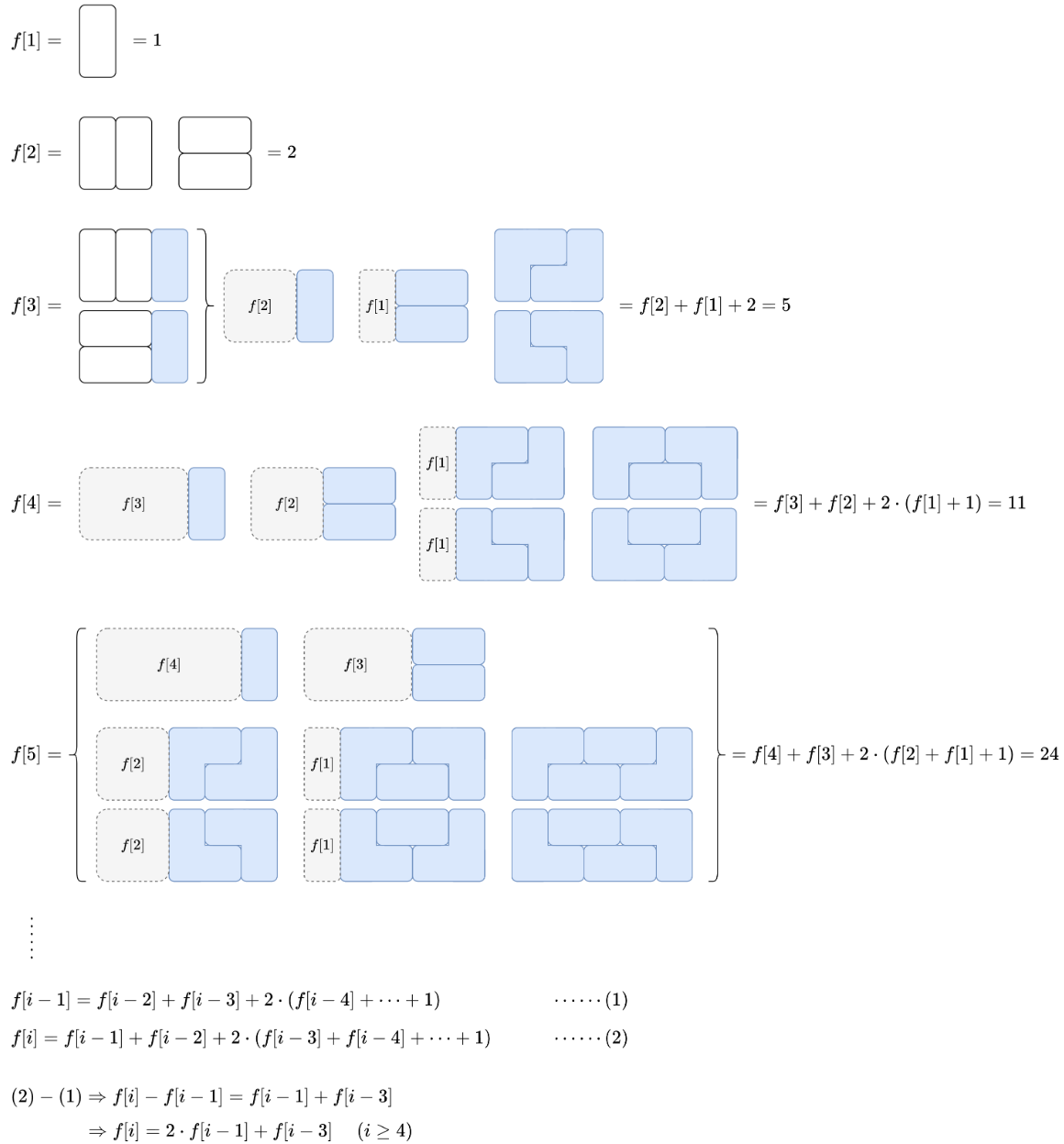
三变量写法

MOD = 1_000_000_007class Solution:def numTilings(self, n: int) -> int:if n == 1:return 1a, b, c = 1, 1, 2for _ in range(3, n + 1):a, b, c = b, c, (c * 2 + a) % MODreturn c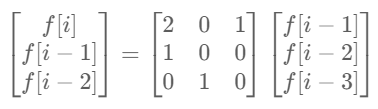

import numpy as npMOD = 10**9 + 7class Solution:def numTilings(self, n: int) -> int:if n == 1:return 1# 构建转移矩阵 M: 3*3M = np.array([[2, 0, 1], [1, 0, 0], [0, 1, 0]], dtype=object)init = np.array([2, 1, 1], dtype=object)# 计算 M^n * initM_power = np.linalg.matrix_power(M, n-2)result = M_power @ initreturn result[0] % MOD

3337. 字符串转换后的长度 II

长度为 26 的 nums 数组，每次 str[i] 替换为字母表后面的 nums[i] 个字母。

比如 nums[24] = 3，每次把字符串中的 y 替换成 zab。

f0 为长度为 26 的初始每个字母的数量。

我要知道 第 i 次变换后 y 对应的长度，也就是 zab 第 i-1 次变换后的长度。

import numpy as np
MOD = 1_000_000_007class Solution:def lengthAfterTransformations(self, s: str, t: int, nums: List[int]) -> int:cnt = Counter(s)f0 = np.array([cnt[c] for c in ascii_lowercase], dtype=object) # 初始矩阵m = np.zeros((26, 26), dtype=object) # 转换矩阵for i, c in enumerate(nums):for j in range(i + 1, i + c + 1):m[i, j % 26] = 1mt = np.linalg.matrix_power(m, t)mt = mt @ f0return np.sum(mt) % MOD

查看全文

http://www.dtcms.com/a/445744.html