近世代数(抽象代数)详细笔记--环
第三章:环
3.1环的定义与基本性质
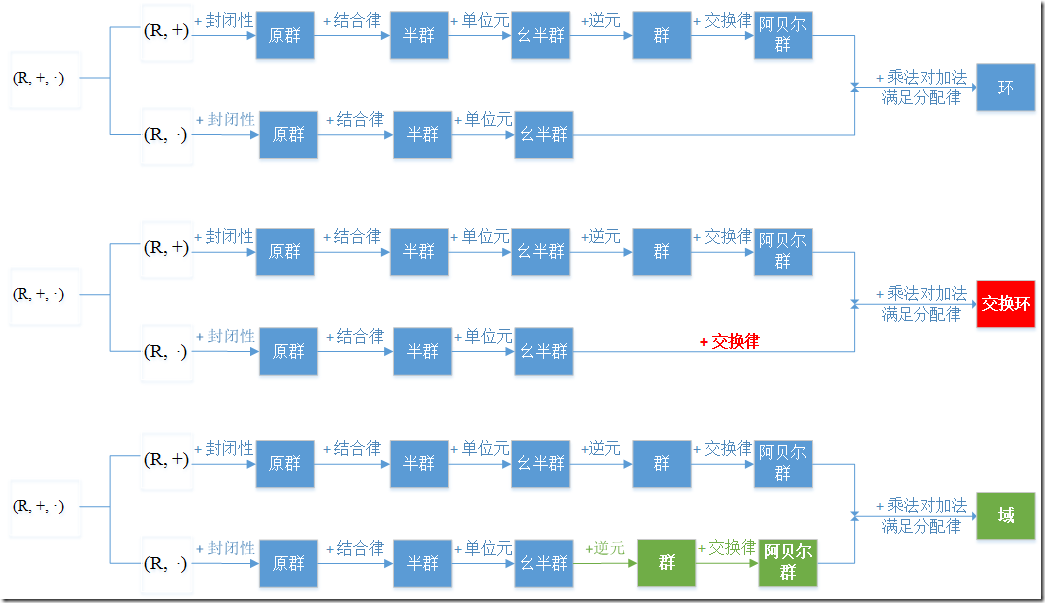
定义:环
设RRR是一个非空集合. 如果在RRR上定义了两个代数运算“+++”(称为加法)和“⋅\cdot⋅”(称为乘法),并且满足
(1) RRR关于加法构成一个交换群;
(2) 乘法结合律成立,即对任意的a,b,c∈Ra,b,c \in Ra,b,c∈R,有 (a⋅b)⋅c=a⋅(b⋅c);(a \cdot b) \cdot c = a \cdot (b \cdot c);(a⋅b)⋅c=a⋅(b⋅c);
(3) 乘法对加法的两个分配律成立,即对任意的a,b,c∈Ra,b,c \in Ra,b,c∈R,有 a⋅(b+c)=a⋅b+a⋅c,a \cdot (b + c) = a \cdot b + a \cdot c,a⋅(b+c)=a⋅b+a⋅c, (b+c)⋅a=b⋅a+c⋅a,(b + c) \cdot a = b \cdot a + c \cdot a,(b+c)⋅a=b⋅a+c⋅a, 则称(R,+,⋅)(R, +, \cdot)(R,+,⋅)为一个环(ring),或简称RRR为环.
注意:目前环的定义中对于乘法构成的运算是否该含有单位元,分成了两个流派。但是目前最常见的是认为环自带单位元,如上的定义
定义:环的可逆元和单位群
设RRR是一个有单位元eee的环,a∈Ra \in Ra∈R。若存在b∈Rb \in Rb∈R,使得ab=ba=eab = ba = eab=ba=e,则称aaa是RRR的一个可逆元(或单位),并称bbb是aaa的逆元。若aaa可逆,则aaa的逆元唯一。
设RRR是一个有单位元的环,其所有可逆元的集合关于环的乘法能构成一个群,这个群称为环RRR的单位群,记为U(R)U(R)U(R)。例如:U(Z)={1,−1}U(\mathbb{Z}) = \{1, -1\}U(Z)={1,−1},U(Q)=Q∗U(\mathbb{Q}) = \mathbb{Q}^*U(Q)=Q∗,U(R)=R∗U(\mathbb{R}) = \mathbb{R}^*U(R)=R∗,U(C)=C∗U(\mathbb{C}) = \mathbb{C}^*U(C)=C∗。
定理:环的运算性质
设 RRR 是一个环,a,b∈Ra,b \in Ra,b∈R,则 (1) a⋅0=0⋅a=0a \cdot 0 = 0 \cdot a = 0a⋅0=0⋅a=0; (2) −(−a)=a-(-a) = a−(−a)=a; (3) a⋅(−b)=(−a)⋅b=−aba \cdot (-b) = (-a) \cdot b = -aba⋅(−b)=(−a)⋅b=−ab; (4) (−a)⋅(−b)=ab(-a) \cdot (-b) = ab(−a)⋅(−b)=ab。
倍数法则:
对任意的 m,n∈Zm,n \in \mathbf{Z}m,n∈Z, a,b∈Ra,b \in Ra,b∈R:
(1) ma+na=(m+n)ama + na = (m + n)ama+na=(m+n)a;
(2) m(a+b)=ma+mbm(a + b) = ma + mbm(a+b)=ma+mb;
(3) m(na)=(mn)a=n(ma)m(na) = (mn)a = n(ma)m(na)=(mn)a=n(ma);
(4) m(ab)=(ma)b=a(mb)m(ab) = (ma)b = a(mb)m(ab)=(ma)b=a(mb).
指数法则:
对任意的 m,n∈Nm,n \in \mathbf{N}m,n∈N, a,b∈Ra,b \in Ra,b∈R:
(1) (am)n=amn(a^m)^n = a^{mn}(am)n=amn;
(2) am⋅an=am+na^m \cdot a^n = a^{m + n}am⋅an=am+n.
注意:
如果 RRR 的元素 aaa 是不可逆的, 则 a0a^0a0 与 a−n(n>0)a^{-n} (n > 0)a−n(n>0) 通常是没有意义的. 同时, 当 ab≠baab \neq baab=ba 时, 等式
(a⋅b)n=an⋅bn(a \cdot b)^n = a^n \cdot b^n(a⋅b)n=an⋅bnS一般也不成立.
应用分配律, 还可以得到下面的广义分配律:
(1) 设 a∈Ra \in Ra∈R, 则对 bi∈R(i=1,2,⋯,n)b_i \in R\ (i = 1,2,\cdots,n)bi∈R (i=1,2,⋯,n), 有 a(∑i=1nbi)=∑i=1nabi,(∑i=1nbi)a=∑i=1nbia.a\left( \sum_{i=1}^n b_i \right) = \sum_{i=1}^n ab_i, \quad \left( \sum_{i=1}^n b_i \right) a = \sum_{i=1}^n b_i a.a(i=1∑nbi)=i=1∑nabi,(i=1∑nbi)a=i=1∑nbia.
(2) 设 ai,bj∈R(i=1,2,⋯,n;j=1,2,⋯,m)a_i, b_j \in R\ (i = 1,2,\cdots,n;\ j = 1,2,\cdots,m)ai,bj∈R (i=1,2,⋯,n; j=1,2,⋯,m), 则 (∑i=1nai)(∑j=1mbj)=∑i=1n∑j=1maibj.\left( \sum_{i=1}^n a_i \right) \left( \sum_{j=1}^m b_j \right) = \sum_{i=1}^n \sum_{j=1}^m a_i b_j.(i=1∑nai)(j=1∑mbj)=i=1∑nj=1∑maibj.
定义:子环
设 (R,+,⋅)(R, +, \cdot)(R,+,⋅) 是一个环,SSS 是 RRR 的一个非空子集。如果 SSS 关于 RRR 的运算构成环,则称 SSS 为 RRR 的一个子环(subring),记作 S<RS < RS<R。
注意:
由定义可知,如果 SSS 是 RRR 的子环,则 (S,+)(S, +)(S,+) 是 (R,+)(R, +)(R,+) 的子加群。因此,RRR 的零元 000 就是 SSS 的零元,SSS 中元素 aaa 在 RRR 中的负元 −a-a−a 就是 aaa 在 SSS 中的负元。
与子群类似,为了判断一个环的非空子集是否构成子环,我们不必按环的定义逐条加以验证。
定理 3.1.2
设RRR是一个环,SSS是RRR的一个非空子集,则SSS是RRR的子环的充分必要条件是:
(1) (S,+)(S, +)(S,+)是(R,+)(R, +)(R,+)的加法子群;
(2) SSS关于RRR的乘法封闭,即对任意的a,b∈Sa, b \in Sa,b∈S,有ab∈Sab \in Sab∈S。
定理 3.1.3
设RRR是一个环,SSS是RRR的一个非空子集,则SSS是RRR的子环的充分必要条件是:
(1) 对任意的a,b∈Sa, b \in Sa,b∈S,a−b∈Sa - b \in Sa−b∈S;
(2) 对任意的a,b∈Sa, b \in Sa,b∈S,ab∈Sab \in Sab∈S。
3.2整环,域与除环
引言:
我们知道,一个具体的群通常是和一个具体的问题联系在一起的。比如,在研究正三角形的对称变换时便得到 S3S_3S3。而环则不同,它的产生常常不只是为了满足某一个特殊问题的需要。更多地,它是作为一种理论的载体,一种进行研究的平台而出现的。比如整数环就是如此。人们利用整数,不仅满足了计算与计数的需要,而且建立并发展了初等数论。所以整数环就是初等数论的一种载体,是进行数论研究的一种平台。数学家们在他们的数学研究中,定义了各种类型的环,以满足不同的需要。其中最常见的,就是整环、域和除环。本节中,我们将分别介绍这几种环。

定义:交换环
(R,+)(R,+)(R,+) 是一个阿贝尔群,(R,⋅)(R,⋅)(R,⋅) 是一个交换幺半群
定义:零因子
设 RRR 为环,a,ba,ba,b 为 RRR 的两个非零元素,如果 a⋅b=0a \cdot b = 0a⋅b=0, 则称 aaa 为 RRR 的一个左零因子(left zero-divisor),bbb 为 RRR 的一个右零因子(right zero-divisor)。左零因子与右零因子统称为零因子。
理解:零因子的破坏性强,阻止我们安心的进行除法操作
有零因子和所有非零元可逆是互斥的
定义:无零因子环
没有零因子的环称为无零因子环
定理:
在一个无零因子的环中,两个消去律成立,即对任意的a,b,c∈Ra,b,c\in Ra,b,c∈R,c≠0c\neq0c=0,如果ac=bcac = bcac=bc或ca=cbca= cbca=cb,则a=ba=ba=b
定义:整环
无零因子有单位元(e≠0e\neq0e=0)的交换环称为整环
注:这里限定e≠0e\neq 0e=0的目的是排除零环(只有一个元素0的环)
定义:除环
设 RRR 是一个有单位元 e≠0e \neq 0e=0 的环. 如果 RRR 中每个非零元都可逆, 则称 RRR 是一个除环(division ring). 非交换的除环称为体(skew field).
定义:域
(R,+)(R,+)(R,+) 是一个阿贝尔群,(R∗,⋅)(R^*,⋅)(R∗,⋅) 也是一个阿贝尔群。R∗R^*R∗表示排除R中去除0
典型的域:
- 有理数域(Q,+,.)(\mathbb{Q}, +,.)(Q,+,.)
- 实数域(R,+,.)(\mathbb{R}, +,.)(R,+,.)
- 复数域(C,+,.)(\mathbb{C}, +,.)(C,+,.)
有限域:
模 p 整数域 (Zp\mathbb{Z}_pZp 或 GF§)
| 封闭 | 单位元 | 逆元 | 交换 | |
|---|---|---|---|---|
| 幺环 | ● | |||
| 交换环 | ● | |||
| 无零因子环 | ● | |||
| 整环 | ● | ● | ● | |
| 除环/体 | ● | ● | ● | |
| 域 | ● | ● | ● | ● |
注意:此处的封闭性指的是非零元乘法的封闭性
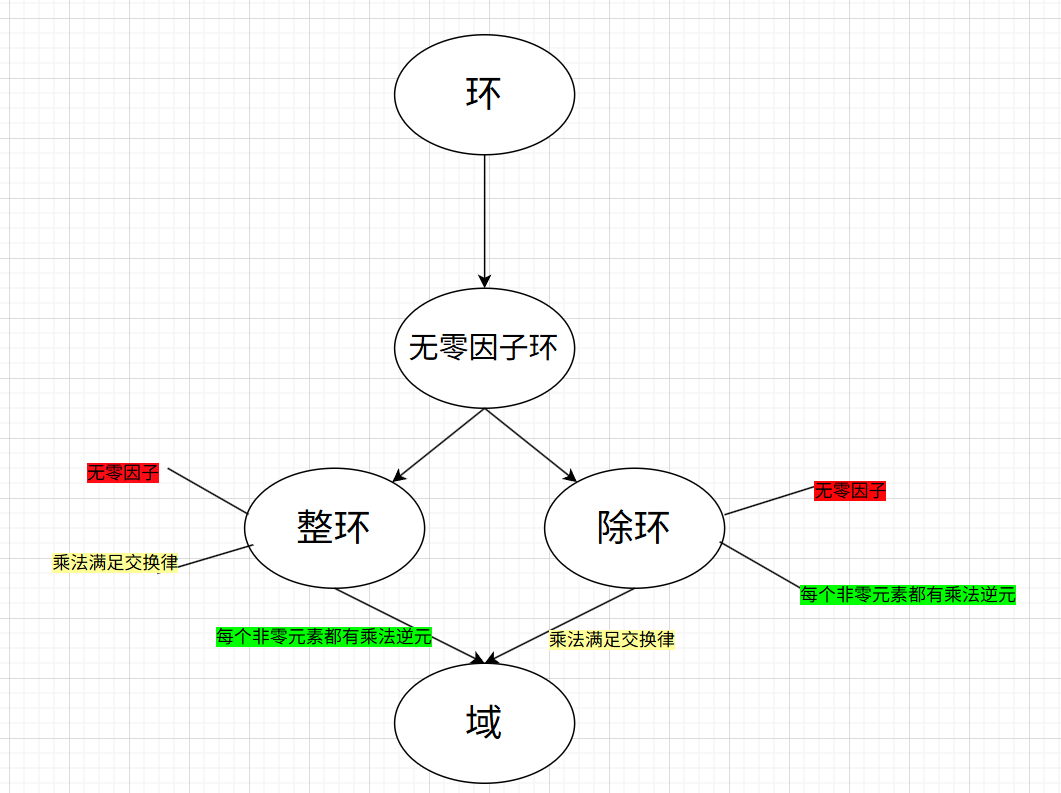
图中的环默认定义有单位元
3.3理想与商环
在群论中,有一类特殊的子群——正规子群,它在群论中扮演着重要的角色。与此类似地,在环论中,也有一类特殊的子环——理想,它在环论中的作用就相当于正规子群在群论中的作用。大家回忆一下,在第2章中,通过正规子群,定义了商群,并进而得到了群的同态定理。在环论中,由理想可以定义商环,并进而有环的同态定理。先来给出理想的定义,讨论它的一些初步性质,然后给出商环的概念。环的同态定理将在3.4节中给出。
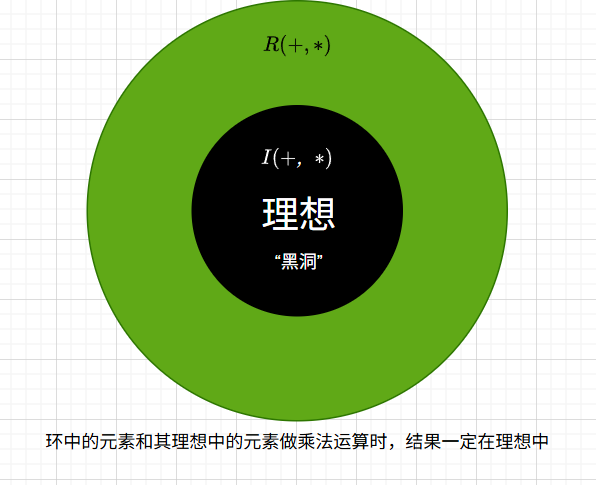
定义:理想
RRR 为环,III 为 RRR 的非空子集,如果 III 满足
(1)对任意的 r1,r2∈Ir_1, r_2 \in Ir1,r2∈I,r1−r2∈Ir_1 - r_2 \in Ir1−r2∈I; (+++构成子群)
(2)对任意的 r∈Ir \in Ir∈I,s∈Rs \in Rs∈R,rs,sr∈Irs, sr \in Irs,sr∈I, 则称 III 为环 RRR 的一个理想(ideal),记作 I◃RI \triangleleft RI◃R。又如果 I⊊RI \subsetneq RI⊊R,则称 III 为 RRR 的真理想(proper ideal)。(吸收)
定义:理想的和与交
设 RRR 为环,I,JI, JI,J 都是 RRR 的理想,集合 I+J={a+b∣a∈I,b∈J}I + J = \{ a + b \mid a \in I, b \in J \}I+J={a+b∣a∈I,b∈J} 与 I∩JI \cap JI∩J 分别称为理想 III 与 JJJ 的和与交。
定理: 3.3.1
设 RRR 为环,I,JI, JI,J 都是 RRR 的理想,则 III 与 JJJ 的和与交都是 RRR 的理想。
定理: 3.3.2
(1) 环 RRR 的任意有限多个理想的和还是 RRR 的理想;
(2) 环 RRR 的任意(有限或无限)多个理想的交还是 RRR 的理想。
定理:主理想(由单个元素生成的理想)
设 RRR 为环,a∈Ra \in Ra∈R,则
(1) ⟨a⟩={∑i=1nxiayi+xa+ay+ma∣xi,yi,x,y∈R,n∈N,m∈Z}\langle a \rangle = \left\{ \sum_{i=1}^{n} x_i a y_i + x a + a y + m a \mid x_i, y_i, x, y \in R, n \in \mathbf{N}, m \in \mathbf{Z} \right\}⟨a⟩={∑i=1nxiayi+xa+ay+ma∣xi,yi,x,y∈R,n∈N,m∈Z}
- 需要包含所有有限和、左倍、右倍及整数倍,以确保对加法和乘法的封闭性。
(2) 如果 RRR 是有单位元的环,则 ⟨a⟩={∑i=1nxiayi∣xi,yi∈R,n∈N}\langle a \rangle = \left\{ \sum_{i=1}^{n} x_i a y_i \mid x_i, y_i \in R, n \in \mathbf{N} \right\} ⟨a⟩={i=1∑nxiayi∣xi,yi∈R,n∈N};
- 单位元 11 的存在允许简化表达式:
- xa=xa⋅1xa = xa \cdot 1xa=xa⋅1,ay=1⋅ayay = 1 \cdot ayay=1⋅ay,ma=m(1⋅a)ma = m(1 \cdot a)ma=m(1⋅a)。
(3) 如果 RRR 是交换环,则
⟨a⟩={xa+ma∣x∈R,m∈Z}\langle a \rangle = \{ x a + m a \mid x \in R, m \in \mathbf{Z} \}⟨a⟩={xa+ma∣x∈R,m∈Z};
- 交换性使得左乘与右乘一致,项 xiayix_i a y_ixiayi 可合并为 (xiyi)a(x_i y_i) a(xiyi)a。
(4) 如果 RRR 是有单位元的交换环,则
⟨a⟩=aR={ar∣r∈R}\langle a \rangle = a R = \{ a r \mid r \in R \}⟨a⟩=aR={ar∣r∈R}。
推论 1 :整数环 Z\mathbb{Z}Z 的每个理想都是主理想。
推论 2 :模 mmm 剩余类环 Zm\mathbb{Z}_mZm 的每个理想都是主理想。
补充:剩余类
设RRR是一个环,III是 R 的一个理想。
对于RRR中的任意一个元素 a,我们定义aaa 模 III 的剩余类为集合:
a+I={a+r∣r∈I}a + I = \{ a + r | r ∈ I \}a+I={a+r∣r∈I}
理解:
剩余类是一种分类方法,将环中所有元素按照它们相对于某个理想(或模某个元素)的“余数”进行分组。
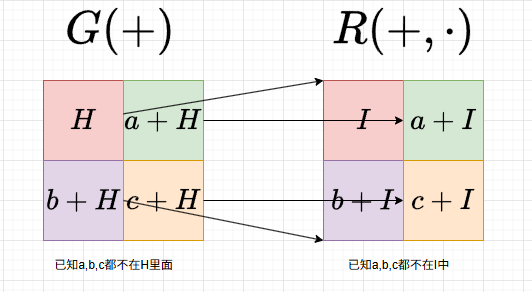
理解:
陪集和剩余类有种一一对应的关系,剩余类只是在陪集的基础上丰富了结构(引入了乘法运算),但是剩余类的本质是建立在陪集之上的概念,因为环的概念就是建立想阿贝尔群上,因为理想这个概念就是建立在正规子群上
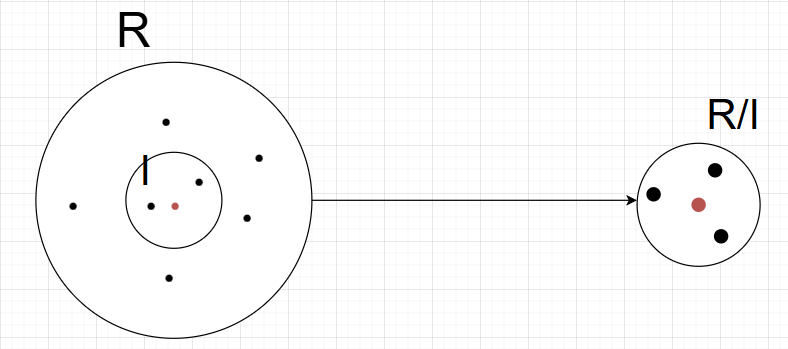
定义:商环
设 RRR 是一个环,III 是环 RRR 的一个理想,则 (I,+)(I, +)(I,+) 是 (R,+)(R, +)(R,+) 的子交换加群,从而 (I,+)(I, +)(I,+) 是 (R,+)(R, +)(R,+) 的正规子群,于是有商群:
R/I={x‾=x+I∣x∈R},R/I = \{ \overline{x} = x + I \mid x \in R \},R/I={x=x+I∣x∈R},
其加法运算定义为
x‾+y‾=x+y‾,x,y∈R.(3.3.1)\overline{x} + \overline{y} = \overline{x + y}, \quad x, y \in R. \tag{3.3.1}x+y=x+y,x,y∈R.(3.3.1)
现在来定义 R/IR/IR/I 的乘法。规定
x‾⋅y‾=xy‾,x,y∈R.(3.3.2)\overline{x} \cdot \overline{y} = \overline{xy}, \quad x, y \in R. \tag{3.3.2}x⋅y=xy,x,y∈R.(3.3.2)
(1) 设 x1,y1,x2,y2∈Rx_1, y_1, x_2, y_2 \in Rx1,y1,x2,y2∈R,且 x1‾=x2‾,y1‾=y2‾\overline{x_1} = \overline{x_2}, \overline{y_1} = \overline{y_2}x1=x2,y1=y2,则 x1−x2,y1−y2∈Ix_1 - x_2, y_1 - y_2 \in Ix1−x2,y1−y2∈I,从而
x1y1−x2y2=x1y1−x1y2+x1y2−x2y2=x1(y1−y2)+(x1−x2)y2∈I.\begin{align*} x_1 y_1 - x_2 y_2 &= x_1 y_1 - x_1 y_2 + x_1 y_2 - x_2 y_2 \\ &= x_1 (y_1 - y_2) + (x_1 - x_2) y_2 \in I. \end{align*} x1y1−x2y2=x1y1−x1y2+x1y2−x2y2=x1(y1−y2)+(x1−x2)y2∈I.
由此得 x1y1‾=x2y2‾\overline{x_1 y_1} = \overline{x_2 y_2}x1y1=x2y2,所以 (3.3.2) 式定义了 R/IR/IR/I 的乘法运算。
(2) 对任意的 x,y,z∈Rx, y, z \in Rx,y,z∈R,
(x‾⋅y‾)⋅z‾=xy‾⋅z‾=xyz‾,x‾⋅(y‾⋅z‾)=x‾⋅yz‾=xyz‾,\begin{align*} (\overline{x} \cdot \overline{y}) \cdot \overline{z} &= \overline{xy} \cdot \overline{z} = \overline{xyz}, \\ \overline{x} \cdot (\overline{y} \cdot \overline{z}) &= \overline{x} \cdot \overline{yz} = \overline{xyz}, \end{align*} (x⋅y)⋅zx⋅(y⋅z)=xy⋅z=xyz,=x⋅yz=xyz,
所以 R/IR/IR/I 关于乘法满足结合律。
(3) 对任意的 x,y,z∈Rx, y, z \in Rx,y,z∈R,
x‾⋅(y‾+z‾)=x‾⋅y+z‾=x(y+z)‾=xy+xz‾=xy‾+xz‾=x‾⋅y‾+x‾⋅z‾,(y‾+z‾)⋅x‾=y+z‾⋅x‾=(y+z)x‾=yx+zx‾=yx‾+zx‾=y‾⋅x‾+z‾⋅x‾,\begin{align*} \overline{x} \cdot (\overline{y} + \overline{z}) &= \overline{x} \cdot \overline{y + z} = \overline{x(y + z)} \\ &= \overline{xy + xz} = \overline{xy} + \overline{xz} \\ &= \overline{x} \cdot \overline{y} + \overline{x} \cdot \overline{z}, \\ (\overline{y} + \overline{z}) \cdot \overline{x} &= \overline{y + z} \cdot \overline{x} = \overline{(y + z)x} \\ &= \overline{yx + zx} = \overline{yx} + \overline{zx} \\ &= \overline{y} \cdot \overline{x} + \overline{z} \cdot \overline{x}, \end{align*} x⋅(y+z)(y+z)⋅x=x⋅y+z=x(y+z)=xy+xz=xy+xz=x⋅y+x⋅z,=y+z⋅x=(y+z)x=yx+zx=yx+zx=y⋅x+z⋅x,
所以 R/IR/IR/I 关于加法与乘法满足两个分配律。
这就证明了,R/IR/IR/I 关于所规定的加法和乘法运算构成环。
3.4环的同态
引言:
研究环可以从两方面入手,一是从环的本身特点、从环的内部结构去研究环,就如在前几节所做的那样;二是从一个环与另一个环的相互关系中去了解环、揭示环的性质.而环与环之间的联系往往是通过环同态来实现的.
定义:环同态
设 RRR 和 R′R'R′ 为两个环,ϕ\phiϕ 是集合 RRR 到 R′R'R′ 的映射.如果对任意的 a,b∈Ra, b \in Ra,b∈R,有
(1) ϕ(a+b)=ϕ(a)+ϕ(b)\phi(a + b) = \phi(a) + \phi(b)ϕ(a+b)=ϕ(a)+ϕ(b);
(2) ϕ(ab)=ϕ(a)ϕ(b)\phi(ab) = \phi(a)\phi(b)ϕ(ab)=ϕ(a)ϕ(b),
则称 ϕ\phiϕ 为环 RRR 到环 R′R'R′ 的一个同态映射(homomorphism),简称同态.
注:由定义可知,环同态就是环之间保持运算的映射.又如果同态映射ϕ\phiϕ是单映射,则称ϕ\phiϕ为单同态(monomorphism);
如果ϕ\phiϕ是满映射,则称ϕ\phiϕ为满同态(epimorphism),此时,称环RRR与R′R'R′同态,记作ϕ:R∼R′\phi: R \sim R'ϕ:R∼R′.
如果ϕ\phiϕ是单射,则称ϕ\phiϕ为单同态(epimorphism)
如果ϕ\phiϕ既是单同态,又是满同态,则称ϕ\phiϕ为同构(isomorphism),此时,称环RRR与R′R'R′同构,记作ϕ:R≅R′\phi: R \cong R'ϕ:R≅R′.
与群的相应概念类似,环的同构是环之间的一个等价关系,并且从环的观点来看,同构的环有完全相同的代数性质.
定义:零同态
设 RRR 与 R′R'R′ 是两个环,定义映射 ϕ:R→R′\phi: R \to R'ϕ:R→R′,对任意 a∈Ra \in Ra∈R,令 a↦0a \mapsto 0a↦0(000 是 R′R'R′ 的零元)。对任意 a,b∈Ra, b \in Ra,b∈R,有 ϕ(a+b)=0=ϕ(a)+ϕ(b)\phi(a + b) = 0 = \phi(a) + \phi(b)ϕ(a+b)=0=ϕ(a)+ϕ(b),且 ϕ(ab)=0=ϕ(a)ϕ(b)\phi(ab) = 0 = \phi(a)\phi(b)ϕ(ab)=0=ϕ(a)ϕ(b),故 ϕ\phiϕ 是 RRR 到 R′R'R′ 的同态,称为零同态。
定义:自然同态
设 RRR 是环,III 是 RRR 的理想,定义映射 η:R→R/I\eta: R \to R/Iη:R→R/I,对任意 a∈Ra \in Ra∈R,令 a↦a‾a \mapsto \overline{a}a↦a(a‾=a+I\overline{a} = a + Ia=a+I 是商环 R/IR/IR/I 中 aaa 对应的陪集)。η\etaη 是满映射,且对任意 a,b∈Ra, b \in Ra,b∈R,有 η(a+b)=a+b‾=a‾+b‾=η(a)+η(b)\eta(a + b) = \overline{a + b} = \overline{a} + \overline{b} = \eta(a) + \eta(b)η(a+b)=a+b=a+b=η(a)+η(b),η(ab)=ab‾=a‾b‾=η(a)η(b)\eta(ab) = \overline{ab} = \overline{a}\overline{b} = \eta(a)\eta(b)η(ab)=ab=ab=η(a)η(b),故 η\etaη 是 RRR 到商环 R/IR/IR/I 的满同态,称为自然同态。
定理: 3.4.1
设ϕ\phiϕ是环RRR到R′R'R′的同态,则对任意的a∈Ra \in Ra∈R,
(1) ϕ(0R)=0R′\phi(0_R) = 0_{R'}ϕ(0R)=0R′;
(2) ϕ(na)=nϕ(a)\phi(na) = n\phi(a)ϕ(na)=nϕ(a),∀n∈Z\forall n \in \mathbb{Z}∀n∈Z;
(3) ϕ(an)=(ϕ(a))n\phi(a^n) = (\phi(a))^nϕ(an)=(ϕ(a))n,∀n∈N\forall n \in \mathbb{N}∀n∈N。
定理:3.4.2
设RRR与R′R'R′都是有单位元的环,eee与e′e'e′分别是它们的单位元,ϕ\phiϕ是RRR到R′R'R′的环同态。
(1) 如果ϕ\phiϕ是满同态,则ϕ(e)=e′\phi(e) = e'ϕ(e)=e′;
(2) 如果R′R'R′为无零因子环,且ϕ(e)≠0\phi(e) \neq 0ϕ(e)=0,则ϕ(e)=e′\phi(e) = e'ϕ(e)=e′;
(3) 如果ϕ(e)=e′\phi(e) = e'ϕ(e)=e′,则对RRR的任一单位uuu,ϕ(u)\phi(u)ϕ(u)是R′R'R′的单位,且(ϕ(u))−1=ϕ(u−1)(\phi(u))^{-1} = \phi(u^{-1})(ϕ(u))−1=ϕ(u−1)。
定义: 3.4.2
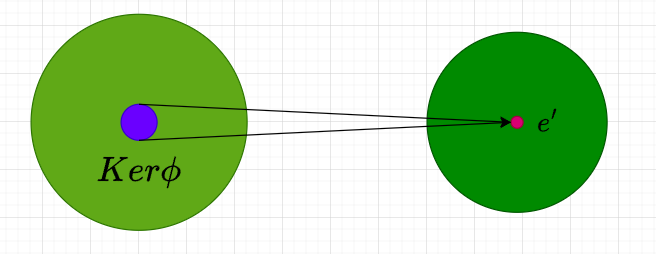
设ϕ\phiϕ为环RRR到环R′R'R′的同态映射。称集合
K={a∈R∣ϕ(a)=0}K = \{a \in R | \phi(a) = 0\}K={a∈R∣ϕ(a)=0}
为环同态ϕ\phiϕ的核(kernel),记作Ker ϕ\text{Ker}\ \phiKer ϕ。
定理:3.4.3
设ϕ\phiϕ为环RRR到R′R'R′的环同态,则Ker ϕ\text{Ker}\ \phiKer ϕ为RRR的理想。
定理: 3.4.4(环同态基本定理)
设ϕ\phiϕ是环RRR到R′R'R′的满同态,则有环同构
ϕ~:R/Ker ϕ≅R′.\tilde{\phi}: R / \text{Ker}\ \phi \cong R'.ϕ~:R/Ker ϕ≅R′.
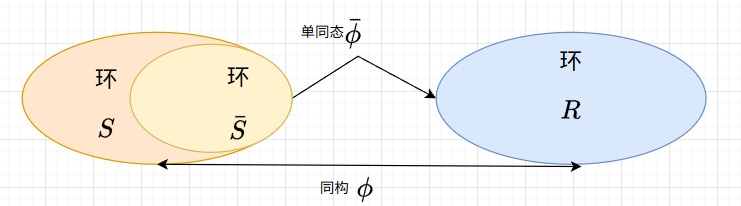
定理:3.4.5(环的扩张定理)
设Sˉ\bar{S}Sˉ与RRR是两个没有公共元素的环,ϕˉ\bar{\phi}ϕˉ是环Sˉ\bar{S}Sˉ到环RRR的单同态,则存在一个与环RRR同构的环SSS及由环SSS到RRR的同构映射ϕ\phiϕ,使Sˉ\bar{S}Sˉ为SSS的子环且**ϕ∣Sˉ=ϕˉ\phi|_{\bar{S}}=\bar{\phi}ϕ∣Sˉ=ϕˉ。**
3.5素理想和极大理想
我们知道,利用一个环的理想,可以构造出新的环——商环.商环在一定程度上继承了原环的一些性质,同时也产生了一些新的特点.这启示我们,如果对环及其理想添加一些不同的限制,就有可能构造出具有不同特点的环来.我们特别感兴趣的是,当RRR及其理想III满足什么条件时,R/IR/IR/I是整环,或者是域?本节的主要目的就是来解决这两个问题.本节的主要内容,特别是有关极大理想的定理,是第5章讨论域的结构的基础.
定义:素理想
设RRR是一个交换环,PPP是RRR的真理想,如果对任意的a,b∈Ra,b \in Ra,b∈R,由ab∈Pab \in Pab∈P,可推出a∈Pa \in Pa∈P或b∈Pb \in Pb∈P,则称PPP为RRR的一个素理想(prime ideal)。
理解:素理想PPP中的任意元素,在任意因子分解中,至少有一个因子在该素理想中:例如在由7生成的素理想<7><7><7>中28可以分解为:2⋅2⋅72\cdot2\cdot72⋅2⋅7或者4⋅74\cdot74⋅7或者2⋅142\cdot142⋅14其中7,7,14在素理想中
结论:<n><n><n>是Z\mathbb{Z}Z的素理想的充分必要条件是nnn为素数。
证明:必要性:如果nnn不是素数,则n=1n=1n=1或nnn为合数.
(1) 如果n=1n=1n=1,则<n>=Z<n>=\mathbb{Z}<n>=Z不是Z\mathbb{Z}Z的素理想.
(2) 如果nnn为合数. 设n=abn=abn=ab,1<a<n1 < a < n1<a<n,1<b<n1 < b < n1<b<n,则a∉<n>a \notin <n>a∈/<n>,b∉<n>b \notin <n>b∈/<n>,而ab=n∈<n>ab = n \in <n>ab=n∈<n>,则(n)(n)(n)也不是Z\mathbb{Z}Z的素理想.
这就证明了必要性.
充分性:设nnn为素数. 如果ab∈<n>ab \in <n>ab∈<n>,则n∣abn \mid abn∣ab. 因为nnn是素数,所以n∣an \mid an∣a或n∣bn \mid bn∣b,即a∈<n>a \in <n>a∈<n>或b∈<n>b \in <n>b∈<n>,所以nnn为素理想.
定理: 3.5.1
设RRR是有单位元e≠0e \neq 0e=0的交换环,III是RRR的理想,则III是RRR的素理想的充分必要条件是R/IR/IR/I是整环。
定义:极大理想
设RRR是一个交换环,MMM是RRR的真理想。如果对RRR的任一包含MMM的理想NNN,必有N=MN = MN=M或N=RN = RN=R,则称MMM为RRR的一个极大理想(maximal ideal)。
结论:⟨p⟩\langle p \rangle⟨p⟩是Z\mathbb{Z}Z的极大理想的充分必要条件是ppp是素数.
设ppp是正整数. 证明: ⟨p⟩\langle p \rangle⟨p⟩是Z\mathbb{Z}Z的极大理想的充分必要条件是ppp是素数.
证明 必要性. 如果ppp不是素数, 则p=1p=1p=1或ppp是一个合数.
(1) 如果p=1p=1p=1, 则⟨p⟩=Z\langle p \rangle = \mathbb{Z}⟨p⟩=Z不是Z\mathbb{Z}Z的极大理想.
(2) 如果ppp是合数, 设p=ab(1<a<p,1<b<p)p=ab(1 < a < p, 1 < b < p)p=ab(1<a<p,1<b<p), 则⟨p⟩⊆⟨a⟩\langle p \rangle \subseteq \langle a \rangle⟨p⟩⊆⟨a⟩. 因为a<pa < pa<p, 所以a∉⟨p⟩a \notin \langle p \ranglea∈/⟨p⟩, 从而⟨p⟩⫋⟨a⟩\langle p \rangle \subsetneqq \langle a \rangle⟨p⟩⫋⟨a⟩. 又因为a>1a > 1a>1, 所以⟨a⟩⫋Z\langle a \rangle \subsetneqq \mathbb{Z}⟨a⟩⫋Z. 因此⟨p⟩\langle p \rangle⟨p⟩也不是Z\mathbb{Z}Z的极大理想.
这就证明了必要性.
充分性. 设ppp是素数, III是Z\mathbb{Z}Z的任一理想, 使⟨p⟩⫋I⊆Z\langle p \rangle \subsetneqq I \subseteq \mathbb{Z}⟨p⟩⫋I⊆Z, 则存在a∈Ia \in Ia∈I, 使a∉⟨p⟩a \notin \langle p \ranglea∈/⟨p⟩. 从而p∤ap \nmid ap∤a. 因为ppp是素数, 所以(a,p)=1(a, p) = 1(a,p)=1. 从而存在u,v∈Zu, v \in \mathbb{Z}u,v∈Z, 使au+pv=1au + pv = 1au+pv=1. 于是, 对任意的z∈Zz \in \mathbb{Z}z∈Z,
z=z⋅1=zau+zpv∈I.z = z \cdot 1 = zau + zpv \in I.z=z⋅1=zau+zpv∈I.
由此得I=ZI = \mathbb{Z}I=Z. 所以⟨p⟩\langle p \rangle⟨p⟩为Z\mathbb{Z}Z的极大理想.
根据例2和例5我们知道, Z\mathbb{Z}Z的非零素理想都是极大理想.
定理:3.5.2
设RRR是有单位元e的交换环,III为RRR的理想,则III是R的极大理想的充分必要条件是:R/IR/IR/I是域。

3.6环的特征与素域
定义:环的特征
设RRR为环. 如果存在最小的正整数nnn,使得对所有的a∈Ra \in Ra∈R,有na=0na = 0na=0,则称nnn为环RRR的特征(Characteristic). 如果这样的正整数不存在,则称环RRR的特征为000. 环RRR的特征记作Char R\text{Char}\ RChar R.
定理:设RRR是有单位元e的环,
- 如果e关于加法的阶无限大,那么RRR的特征等于0
- 如果e关于加法的阶等于n,那么char R= n;
理解:环的特征特征等于单位元eee在加法下的阶
定理:整环的特征是0或者是一个素数
定理 :设RRR是有单位元eee的环,则映射
ϕ:Z→R,\phi: \mathbb{Z} \to R,ϕ:Z→R,
n↦nen \mapsto nen↦ne
是环Z\mathbb{Z}Z到RRR的同态。
理解:ϕ\phiϕ将每个整数nnn映为nenene,其中nenene表示单位元eee在环RRR中加几次。
推论 设RRR是有单位元的环.
(1) 如果RRR的特征为n>0n > 0n>0,则RRR包含一个与Zn\mathbb{Z}_nZn同构的子环;
(2) 如果RRR的特征为000,则RRR包含一个与Z\mathbb{Z}Z同构的子环.
理解:
该推论建立了抽象环与具体数系之间的桥梁
特征直接决定了环中所包含的最基本的算术系统类型
在域论中该推论有直接的应用,任何一个域FFF都包含一个素域
特征直接决定了环中所包含的最基本的算术系统类型,这个怎么理解??这个群只是包含一个和Z_n或者Z同构在子环,又不是直接和Z_n和Z同构了 1.在任何有单位元e的环R中,由单位元生成的子环<1>={n.1|n属于Z}是R的 最小子环, 2.特征决定了环的素子环的结构,而素子环是环的算术基础。即使环本身更大,其整体运算规则也必须与素子环的规则兼容。因此,特征确实决定了环中最基本的算术系统类型。您的观察是正确的——环不一定直接同构于 $Z$ 或 $Z_n$,但通过素子环,特征对环的算术产生了全局性的影响。 **定义**: 素域一个域FFF如果不含任何真子域,则称FFF是一个素域(prime field)。
理解:将素域想象成域世界的“原子”——它不能再被分解为更小的域。所有域都是由素域通过添加元素(如代数元或超越元)构建而成的。这类似于整数中素数的作用:所有整数都可以由素数构建。
| 概念名称 | 所属代数结构 | 生成元素 | 结构形式(分情况) | 最小性体现 |
|---|---|---|---|---|
| 素子域 | 域 | 域的单位元 111 | 1. 特征为 000:同构于有理数域 Q\mathbb{Q}Q 2. 特征为素数 ppp:同构于有限域 Z/pZ\mathbb{Z}/p\mathbb{Z}Z/pZ | 被包含在域的所有子域中,是域的最小子域 |
| 含幺环的最小子环 | 含幺环 | 环的单位元 111 | 1. 特征为 000:同构于整数环 Z\mathbb{Z}Z 2. 特征为 nnn:同构于商环 Z/nZ\mathbb{Z}/n\mathbb{Z}Z/nZ | 被包含在环的所有含幺子环中,是环的最小含幺子环(不含幺环不适用) |
| 循环子群 | 群 | 群中任意元素 ggg | 1. 乘法群:⟨g⟩={gn∣n∈Z}\langle g \rangle = \{ g^n \mid n \in \mathbb{Z} \}⟨g⟩={gn∣n∈Z} 2. 加法群:⟨g⟩={ng∣n∈Z}\langle g \rangle = \{ ng \mid n \in \mathbb{Z} \}⟨g⟩={ng∣n∈Z} | 被包含在所有包含元素 ggg 的子群中,是含 ggg 的最小子群 |
第四章:环的进阶
引言:
整数环Z\mathbb{Z}Z与数域FFF上的多项式环F[x]F[x]F[x]是两类最重要且应用最广的环。其之所以重要,是因为在这两类环上有所谓整除的概念,并由此建立了数论与多项式理论。本章将在一般的整环上讨论整除的概念以及多项式的概念,并建立相应的理论。4.1 节建立一般环上的多项式的概念。4.2 节给出整环的商域的概念。4.3 节、4.4 节讨论整环上的整除理论,这是本章的中心内容。4.5 节讨论唯一分解整环上的多项式环的整除问题。
4.1多项式环
本节的主要目的是把多项式的概念从系数取自数域推广到系数取自一般的有单位元的环上. 说到多项式, 读者自然会想到形如
f(x)=3x4−2x3+x2+x−2f(x) = 3x^4 - 2x^3 + x^2 + x - 2f(x)=3x4−2x3+x2+x−2
的表达式, 其中 3,−2,1,1,−23, -2, 1, 1, -23,−2,1,1,−2 称为多项式 f(x)f(x)f(x) 的系数。 如果 f(x)f(x)f(x) 的系数属于某个数域 FFF(或数环 DDD), 就称 f(x)f(x)f(x) 为数域 FFF(或数环 DDD) 上的多项式. 在第 3 章中, 也曾讨论过剩余类域 Zp\mathbb{Z}_pZp(ppp 为素数) 上的多项式. 对于一个多项式 f(x)f(x)f(x), 它的系数是很明确的. 但如果问: 这其中的 xxx 是什么? 却很难简单地说清楚. 不说别的, 就是对 xxx 的称呼, 也是五花八门, 众说纷纭. 有的把它叫做一个符号; 有的把它叫做一个文字; 还有的则把它叫做一个变量, 等等。这样, 如果不把 xxx 的真实身份搞清楚, 我们总有一种捉摸不定的感觉, 但这还不是最重要的。关键是, 如果在对 xxx 的真实意义都还没有彻底弄清楚的情况下, 怎能确信由此而得到的多项式在理论上是毫无缺陷的呢? 为了能够把多项式的概念推广到一般的环上, 首先必须揭开遮在 xxx 上的这一层神秘面纱。
定义: 未定元
设RRR是一个有单位元的环,Rˉ\bar{R}Rˉ是RRR的扩环,xxx是Rˉ\bar{R}Rˉ中的一个元素。如果xxx满足
(1) 对任意的r∈Rr \in Rr∈R,xr=rxxr = rxxr=rx;
(2) 1x=x1x = x1x=x;
(3) 对RRR的任意一组不全为零的元素a0,a1,⋯,ana_0, a_1, \cdots, a_na0,a1,⋯,an,
f(x)=a0+a1x+a2x2+⋯+anxn≠0,f(x) = a_0 + a_1x + a_2x^2 + \cdots + a_nx^n \neq 0,f(x)=a0+a1x+a2x2+⋯+anxn=0,
则称xxx为RRR上的一个未定元(indeterminate).
正确理解:
在未定元的定义中,元素 xxx 不是变量,它是扩环 Rˉ\bar{R}Rˉ 中的一个特定元素。条件(3)的意思是:对于这个固定的 xxx,任何系数不全为零的多项式 fff(即系数 a0,a1,…,an∈Ra_0, a_1, \dots, a_n \in Ra0,a1,…,an∈R 不全为零),当将 xxx 代入多项式时,得到的值 f(x)f(x)f(x) 不等于扩环 Rˉ\bar{R}Rˉ 中的零元素(即 f(x)≠0Rˉf(x) \neq 0_{\bar{R}}f(x)=0Rˉ)。
错误理解:
这个定义的意思是如果元素a0,a1,⋯,ana_0, a_1, \cdots, a_na0,a1,⋯,an不全为零,那么无论xxx取Rˉ\bar{R}Rˉ中什么值,该式子都不等于零
定理:未定元的存在性定理
设RRR是一个有单位元的环,则一定存在环RRR上的一个未定元xxx。
定义:幂级数环
形如:
a0+a1x+a2x2+⋯+anxn+⋯a_0 + a_1x + a_2x^2 + \cdots + a_nx^n + \cdotsa0+a1x+a2x2+⋯+anxn+⋯
的表达式(称为环RRR上的形式幂级数)所组成的环,这个环称为环RRR上的形式幂级数环(formal power series ring),记作R[[x]]R[[x]]R[[x]]。环RRR上的形式幂级数环在组合数学中有重要应用。
定义:一元多项式
设 RRR 是一个有单位元的环,xxx 是 RRR 上的一个未定元,a0,a1,a2,…,an∈Ra_0, a_1, a_2, \dots, a_n \in Ra0,a1,a2,…,an∈R。称形如 f(x)=a0+a1x+a2x2+⋯+anxnf(x) = a_0 + a_1 x + a_2 x^2 + \dots + a_n x^nf(x)=a0+a1x+a2x2+⋯+anxn 的表达式为 RRR 上(关于 xxx 的)一元多项式 (polynomial),其中 aixia_i x^iaixi 称为多项式 f(x)f(x)f(x) 的 iii 次项 (term),aia_iai 称为 iii 次项的系数,a0a_0a0 也称为常数项(constant term)。如果 an≠0a_n \neq 0an=0,则称 ana_nan 为首项系数(leading coefficient),并称 f(x)f(x)f(x) 的次数为 nnn,记作 degf(x)=n\deg f(x) = ndegf(x)=n。系数全为零的多项式称为零多项式,零多项式不规定次数。
定义:多项式环
设 RRR 是一个有单位元的环,xxx 是 RRR 上的一个未定元。称环 R[x]R[x]R[x] 为 RRR 上的以 xxx 为未定元的一元多项式环(polynomial ring),简称多项式环。
注意:在一元多项式环R[x]R[x]R[x]中多项式的次数n是不确定的
理解:这个定义结合未定元的存在性定理可以知道,对于任意一个有单位元的环,一定存在其上的一个一元多项式环
定理 :4.1.2
设 RRR 与 R′R'R′ 是两个有单位元的环,xxx 与 yyy 分别是其上的未定元。如果 R≅R′R \cong R'R≅R′,则R[x]≅R′[y]R[x] \cong R'[y]R[x]≅R′[y]。
定理: 4.1.3
设 RRR 是一个有单位元的环,xxx 是 RRR 上的一个未定元。
(1) RRR 的零元 000 就是 R[x]R[x]R[x] 的零元 (即零多项式);
(2) R[x]R[x]R[x] 是有单位元的环,且 RRR 的单位元就是 R[x]R[x]R[x] 的单位元;
(3) 如果 RRR 是无零因子环,则 R[x]R[x]R[x] 也是无零因子环,且 R[x]R[x]R[x] 的单位就是 RRR 的单位;
(4) 如果 RRR 是交换环,则 R[x]R[x]R[x] 也是交换环;
(5) 如果 RRR 是整环,则 R[x]R[x]R[x] 也是整环。
理解:R[x]R[x]R[x] 是包含环 RRR 和一个新未定元 xxx 的最小环,其中 RRR 可以视为 R[x]R[x]R[x] 中常数多项式构成的子环。
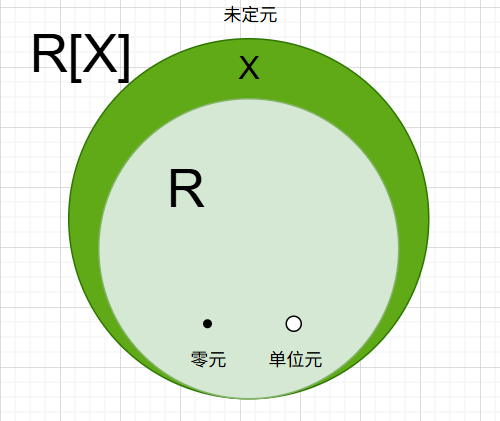
图解:共用同一零元和单位元,都是“圆形”表示结构一致
多项式环R[x]与形式幂级数环R[[x]]核心差异表
| 对比维度 | 多项式环 R[x] | 形式幂级数环 R[[x]] |
|---|---|---|
| 符号表示 | 单中括号 [ ] | 双中括号 [[ ]] |
| 核心定义 | 系数取自环 R 的有限项多项式构成的代数结构 | 系数取自环 R 的无限项形式和构成的代数结构 |
| 元素具体形式 | 有限和:a0+a1x+⋯+anxna_0 + a_1x + \cdots + a_nx^na0+a1x+⋯+anxn(n 为有限整数) | 无限和:a0+a1x+a2x2+⋯a_0 + a_1x + a_2x^2 + \cdotsa0+a1x+a2x2+⋯(无终止项) |
| 代数运算复杂度 | 运算简单,仅需处理有限项的加减乘 | 运算复杂,需按规则处理无限项的加减乘(形式上封闭) |
| 可逆性示例(以 ℤ 为例) | 如 1−x1-x1−x 不一定可逆(无有限项多项式作为其逆) | 如 1−x1-x1−x 可逆,逆为 1+x+x2+⋯1 + x + x^2 + \cdots1+x+x2+⋯(无限和) |
| 核心关注点 | 多项式的代数运算(无收敛性相关考量) | 系数的纯代数运算(不关心级数是否收敛) |
| 典型应用场景 | 多项式因式分解、多项式方程求解等基础代数问题 | 组合数学中的生成函数、代数结构分析等 |
4.2整环的商域
引言:
在一个有单位元的环中,并不是每个非零元都是可逆的。例如,在整数环中,可逆元仅有±1\pm1±1,这使得像2x=12x = 12x=1这样的方程在整数环中就没有解。为了使方程ax=b(a≠0)ax = b(a \neq 0)ax=b(a=0)都有解,必须把整数环扩充为有理数域,也就是说,必须由整数环出发,去构造一个更大的代数 体系——有理数域。我们知道,有理数域是由所有形如ab(a,b∈Z,b≠0)\frac{a}{b}(a,b \in \mathbb{Z},b \neq 0)ba(a,b∈Z,b=0)的分数所组成的,并且它还以整数环作为它的子环。这启发我们,对一般的环,是否也可以把它扩充为一个更大的环,使其上每个非零元都可逆?答案是否定的。比如,对于一个有零因子的环(有零因子的环扩充之后也是包含零因子的,然而域肯定是非零因子的环),这样的扩充显然是不可能的,所以如果一个环RRR可被一个除环或域所包含,则它必须是无零因子环,但当RRR是非交换环时,这一条件还是不够充分的。因为有例子说明,一个无零因子的非交换环不一定能被一个除环所包含,但对于整环,这一点却是可以实现的。本节将采用与由整数构造分数(整数环Z\mathbb{Z}Z构造有理数域Q\mathbb{Q}Q)相类似的方法,将整环扩充为一个域。
整环构造域的证明 设$D$是整环,$1$是$D$的单位元。我们从$D$出发,分几步来完成这样的构造。 ### 1. 构作集合$S$ 令 $$S = \{(a,b) \mid a,b \in D, b \neq 0\}.$$ ### 2. 在$S$上定义一个等价关系 对任意的$(a,b), (c,d) \in S$,令 $$(a,b) \sim (c,d) \iff ad = bc.$$ - **反身性**:由$ab = ba$,得$(a,b) \sim (a,b)$; - **对称性**:若$(a,b) \sim (c,d)$,则$ad = bc$,从而$cb = da$,故$(c,d) \sim (a,b)$; - **传递性**:设$(a,b) \sim (c,d)$且$(c,d) \sim (e,f)$,则$ad = bc$且$cf = de$,相乘得$adcf = bcde \tag{4.2.1}$。若$c = 0$,则$a = e = 0$,故$af = be$;若$c \neq 0$,由整环消去律得$af = be$。因此$(a,b) \sim (e,f)$。 综上,“$\sim$”是$S$的等价关系。 ### 3. 由等价关系得到商集$F$ 对任意$(a,b) \in S$,记其等价类为 $$\left[ \frac{a}{b} \right] = \{(c,d) \in S \mid (c,d) \sim (a,b)\}.$$ 令商集 $$F = S / \sim = \left\{ \left[ \frac{a}{b} \right] \mid a,b \in D, b \neq 0 \right\},$$ 则等价类相等的充要条件为: $$\left[ \frac{a}{b} \right] = \left[ \frac{c}{d} \right] \iff ad = bc.$$ ### 4. 定义$F$的运算,使$F$构成一个域 对任意$\left[ \frac{a}{b} \right], \left[ \frac{c}{d} \right] \in F$,规定: - 加法:$\left[ \frac{a}{b} \right] + \left[ \frac{c}{d} \right] = \left[ \frac{ad + bc}{bd} \right]$; - 乘法:$\left[ \frac{a}{b} \right] \cdot \left[ \frac{c}{d} \right] = \left[ \frac{ac}{bd} \right]$。 #### 验证运算良定性(与代表元无关) 若$\left[ \frac{a'}{b'} \right] = \left[ \frac{a}{b} \right]$且$\left[ \frac{c'}{d'} \right] = \left[ \frac{c}{d} \right]$,则$a'b = ab'$,$c'd = cd'$。可证: $$\left[ \frac{ad + bc}{bd} \right] = \left[ \frac{a'd' + b'c'}{b'd'} \right], \quad \left[ \frac{ac}{bd} \right] = \left[ \frac{a'c'}{b'd'} \right],$$ 故加法、乘法是$F$的代数运算。 #### 验证域的公理 1. **结合律**:加法和乘法均满足结合律(通过分式运算验证); 2. **交换律**:加法和乘法均满足交换律; 3. **分配律**:乘法对加法满足分配律; 4. **零元**:$\left[ \frac{0}{1} \right]$是$F$的零元(记为$0_F$); 5. **单位元**:$\left[ \frac{1}{1} \right]$是$F$的单位元(记为$1_F$),且$0_F \neq 1_F$; 6. **负元**:对任意$\left[ \frac{a}{b} \right]$,$\left[ \frac{-a}{b} \right]$是其负元; 7. **逆元**:对任意$\left[ \frac{a}{b} \right] \neq 0_F$,$\left[ \frac{b}{a} \right]$是其逆元。 因此,$F$是一个域。 ### 5. 由$F$构作一个包含$D$的域 定义映射$\phi: D \to F$,$x \mapsto \left[ \frac{x}{1} \right]$: - **单射**:若$\left[ \frac{x}{1} \right] = \left[ \frac{y}{1} \right]$,则$x = y$; - **同态**:$\phi(x + y) = \phi(x) + \phi(y)$,$\phi(xy) = \phi(x) \cdot \phi(y)$。 由环的扩张定理(定理3.4.5),因$D \cap F = \varnothing$,存在$D$的扩环$Q$及环同构$\tilde{\phi}: Q \cong F$。又$F$是域,故$Q$也是域。 ### 6. $Q$的元素的表达式 因为域$Q$包含$D$,所以也包含$D$中非零元的逆元及它们的乘积,因此$Q$必包含全体形如 $$ab^{-1},\ a,b \in D,\ b \neq 0$$ 的元素。 对任意$\left[ \frac{a}{b} \right] \in F$,由环扩张定理的证明及$\phi$的定义,有: $$\tilde{\phi}^{-1}\!\left( \left[ \frac{a}{b} \right] \right) = \tilde{\phi}^{-1}\!\left( \left[ \frac{a}{1} \right] \cdot \left[ \frac{1}{b} \right] \right)$$ $$= \tilde{\phi}^{-1}\!\left( \left[ \frac{a}{1} \right] \right) \cdot \tilde{\phi}^{-1}\!\left( \left[ \frac{1}{b} \right] \right)$$ $$= \tilde{\phi}^{-1}\!\left( \left[ \frac{a}{1} \right] \right) \cdot \tilde{\phi}^{-1}\!\left( \left( \left[ \frac{b}{1} \right] \right)^{-1} \right)$$ $$= a \left( \tilde{\phi}^{-1}\!\left( \left[ \frac{b}{1} \right] \right) \right)^{-1}$$ $$= ab^{-1}.$$ 这说明$Q$的每个元素都可表为$ab^{-1}\ (a,b \in D,\ b \neq 0)$的形式,故 $$Q = \{ ab^{-1} \mid a,b \in D,\ b \neq 0 \}.$$ 因$Q$是域,记$\frac{a}{b} = ab^{-1}$,则 $$Q = \left\{ \frac{a}{b} \mid a,b \in D,\ b \neq 0 \right\}.$$定理:每一个整环都可以扩充为一个域。
定义:商域
设 DDD是一个整环,则存在一个包含DDD(或与 DDD 同构的环)的最小域 FFF,称为DDD 的商域(或分式域)。
定理:
设DDD与D′D'D′是同构的两个整环,则它们的商域也同构。

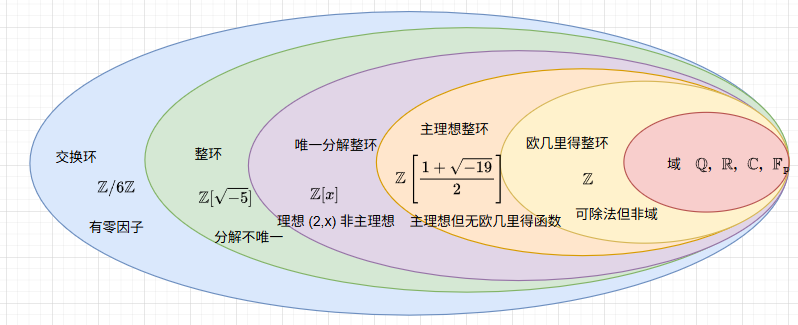
4.3唯一分解整环
引言:
在整数环 Z\mathbb{Z}Z 上,有如下所谓的算术基本定理:
不计因子的次序,每一个大于 111 的正整数可唯一分解为素数的乘积。 这个定理之所以基本,是因为数论中的许多结论都基于这个定理。我们自然要问,能否把这个定理推广到一般的环上,特别是推广到整环上,从而进一步把整数环中的相关概念与定理也推广到整环上呢?答案是否定的,但如果给整环加以一定的限制,则这种推广还是部分地可达到的。本节及随后两节的目的,就是要对整环中的整除性和唯一分解问题作一些讨论。 在本节及随后的几节中,以 DDD 表示整环,FFF 表示整环 DDD 的商域,UUU 表示 DDD 的单位群,111 与 000 分别表示 DDD 的单位元与零元。 首先讨论整除的概念。
定义:因子
设 DDD 是整环,a,b∈Da,b \in Da,b∈D。如果存在 c∈Dc \in Dc∈D,使 a=bca = bca=bc,则称 bbb 是 aaa 的一个因子(divisor),并称 aaa 能被 bbb 整除,或 bbb 整除 aaa,记作 b∣ab \mid ab∣a。如果 bbb 不是 aaa 的因子,则称 aaa 不能被 bbb 整除(我觉着这里说分解比较贴切,但是仅仅限于记忆理解),或 bbb 不整除 aaa,记作 b∤ab \nmid ab∤a。
**定理 ** 4.3.1
在整环 DDD 中
(1) 如果 a∣ba \mid ba∣b,则对任一 u∈Uu \in Uu∈U,有 au∣bau \mid bau∣b;
(2) 如果 a∣ba \mid ba∣b,且 a∣ca \mid ca∣c,则对任意的 x,y∈Dx,y \in Dx,y∈D,有 a∣bx+cya \mid bx + cya∣bx+cy;
(3) 如果 a∣ba \mid ba∣b,且 b∣cb \mid cb∣c,则 a∣ca \mid ca∣c。
理解:
(1)b=(au)⋅(u−1q)b=(au)\cdot (u^{-1}q)b=(au)⋅(u−1q),u−1q∈Du^{-1}q\in Du−1q∈D,所以auauau也整除bbb
(2)由 a∣ba \mid ba∣b 和 a∣ca \mid ca∣c,存在 q1,q2∈Dq_1, q_2 \in Dq1,q2∈D 使得 b=aq1b = aq_1b=aq1,c=aq2c = aq_2c=aq2。那么 bx+cy=aq1x+aq2y=a(q1x+q2y)bx + cy = aq_1 x + aq_2 y = a(q_1 x + q_2 y)bx+cy=aq1x+aq2y=a(q1x+q2y),所以 aaa 整除 bx+cybx + cybx+cy。
定义:相伴
设 DDD 是整环,a,b∈Da,b \in Da,b∈D。如果 a∣ba \mid ba∣b,且 b∣ab \mid ab∣a,则称 aaa 与 bbb 相伴,记作 a∼ba \sim ba∼b。
**定理 ** 4.3.2
设 DDD 是整环,a,b∈Da,b \in Da,b∈D,则下列条件等价:
(1) a∼ba \sim ba∼b;
(2) ⟨a⟩=⟨b⟩\langle a \rangle = \langle b \rangle⟨a⟩=⟨b⟩;
(3) 存在单位 u∈Du \in Du∈D,使 a=bua = bua=bu。
注意:环中的可逆元素称为单位。
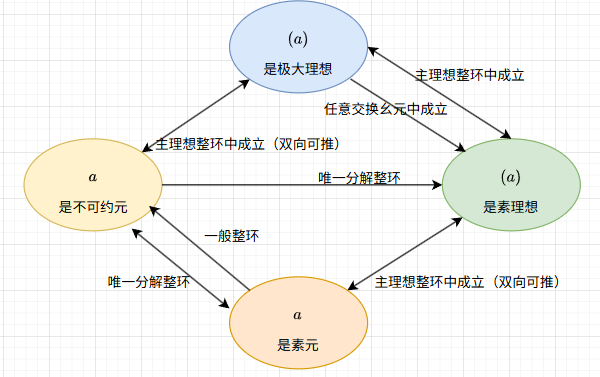
定义 :不可约元
整环 DDD 中非零非单位且无真因子的元素称为 DDD 的不可约元(irreducible element)。
注非零元非可逆并且没有真因子的元素
定义: 素元
设 ppp 是整环 DDD 的一个非零非单位的元素,如果对任意的 a,b∈Da,b \in Da,b∈D,由 p∣abp \mid abp∣ab 可推出 p∣ap \mid ap∣a 或 p∣bp \mid bp∣b,则称 ppp 为 DDD 的一个素元(prime element)。
显然:素元ppp的每一个相伴元也都是素元
理解: “素元” 和 “不可约元” 都是由素数的性质推广得到的.
不过这个推广并不按套路出牌,唉,是真的一言难尽!
素数有两条性质:
(1)只有 1 和它本身这两个因子
(2)p∣ab⇒p∣ap|ab \Rightarrow p|ap∣ab⇒p∣a 或 p∣bp|bp∣b
素数是由性质(1)定义的
但是 “素数” 的推广概念 “素元” 却是由性质(2)定义的
性质(1)定义的反而是 “不可约元”.
另外,在整数环中,性质(1)和性质(2)等价
但是推广后(1)和(2)却不等价(唯一因子分解整环中等价)
定理:4.3.3
在整数环(Z\mathbb{Z}Z)中,每一个素数既是素元也是不可约元
推广:在整环中每一个素元都是不可约元,但是反之不一定正确
定义 : 不可约分解的唯一性
设 DDD 是一个整环,aaa 是 DDD 的一个非零非单位的元素。
(1) 如果存在有限多个不可约元 p1,p2,⋯,psp_1,p_2,\cdots,p_sp1,p2,⋯,ps(s⩾1s \geqslant 1s⩾1),使
a=p1p2⋯ps,a = p_1 p_2 \cdots p_s,a=p1p2⋯ps,
则称 aaa 有不可约分解,并称上述分解式为 aaa 的一个不可约分解。
(2) 如果 aaa 有不可约分解,并且 aaa 的不可约分解在相伴的意义下是唯一的,即如果 aaa 有两个不可约分解
a=p1p2⋯ps=q1q2⋯qt,a = p_1 p_2 \cdots p_s = q_1 q_2 \cdots q_t,a=p1p2⋯ps=q1q2⋯qt,
则 s=ts = ts=t,并且适当交换因子的次序,有
pi∼qi,i=1,2,⋯,s,p_i \sim q_i, \quad i = 1,2,\cdots,s,pi∼qi,i=1,2,⋯,s,
则称 aaa 有唯一分解。
定义:唯一分解整环
设DDD是一个整环,如果DDD中的每一个非零非单位的元素都有唯一的分解,则称DDD为唯一分解整环(unique factorization domain),记作UFD
定理:4.3.5
在唯一分解整环中,每一个不可约元都是素元。
定义 真因子链
设 DDD 是整环,
a1,a2,⋯,an,⋯(4.3.4)a_1, a_2, \cdots, a_n, \cdots \tag{4.3.4}a1,a2,⋯,an,⋯(4.3.4)
是 DDD 中的一列元素 (有限或无限)。如果对任意的 i>1i > 1i>1,aia_iai 为 ai−1a_{i-1}ai−1 的真因子,则称元素列 (4.3.4) 为 DDD 的一个真因子链(chain of proper divisors)。
定理 :4.3.6
在唯一分解整环中,每一个真因子链都是有限的。
定理:4.3.7
整环DDD是唯一分解整环的充分必要条件是:
(1)DDD中的每一个真因子链都是有限;
(2)DDD的每一个不可约元都是素元。
定义:标准分解式
设 DDD 是唯一分解整环,aaa 是 DDD 的一个非零非单位的元素,则 aaa 有唯一分解。设 aaa 的所有互不相伴的不可约因子为
p1,p2,⋯,ps,p_1, p_2, \cdots, p_s,p1,p2,⋯,ps,
则对 aaa 的任一不可约因子 ppp,有 pip_ipi,使
p∼pi.p \sim p_i.p∼pi.
从而 aaa 的分解式可表示为
a=ϵp1r1p2r2⋯psrs,(4.3.7)a = \epsilon p_1^{r_1} p_2^{r_2} \cdots p_s^{r_s} \tag{4.3.7},a=ϵp1r1p2r2⋯psrs,(4.3.7)
其中 ϵ\epsilonϵ 为 DDD 的单位,r1,⋯,rs∈Nr_1, \cdots, r_s \in \mathbb{N}r1,⋯,rs∈N。称上式为 aaa 的标准分解式。
定理:4.3.8
在唯一分解整环中,任何两个元素都有最大的公因子
定义 :互素
设 DDD 是一个整环,a,b∈Da,b \in Da,b∈D。如果 gcd(a,b)=1\gcd(a,b)=1gcd(a,b)=1,则称 aaa 与 bbb 互素(coprime)。
定理 4.3.9
设 DDD 为唯一分解整环,a,b,c∈Da,b,c \in Da,b,c∈D 且 gcd(a,b)=1\gcd(a,b)=1gcd(a,b)=1,则
(1) 如果 a∣bca \mid bca∣bc,则 a∣ca \mid ca∣c;
(2) 如果 a∣ca \mid ca∣c 且 b∣cb \mid cb∣c,则 ab∣cab \mid cab∣c;
(3) gcd(a,c)gcd(b,c)=gcd(ab,c)\gcd(a,c)\gcd(b,c)=\gcd(ab,c)gcd(a,c)gcd(b,c)=gcd(ab,c)。
4.4主理想整环与欧几里得整环
定义:主理想整环
设 DDD 是一个整环,如果 DDD 的每一个理想都是主理想,则称 DDD 为主理想整环(principal ideal domain),记作 PID。
定理:4.4.1
每一个主理想整环都是唯一分解整环
定理:4.4.2
设DDD是一个主理想整环,则DDD上的每一个真因子链都有限
定理 :4.4.3
设 aaa 是主理想整环 DDD 的一个非零非单位的元素,则下列条件等价:
(1) aaa 是素元;
(2) aaa 是不可约元;
(3) ⟨a⟩\langle a \rangle⟨a⟩ 是极大理想;
(4) ⟨a⟩\langle a \rangle⟨a⟩ 是素理想。
**定理 **4.4.4(最大公因子的存在表示定理)
设 DDD 是一个主理想整环,则对任意的 a,b∈Da,b \in Da,b∈D,存在 u,v∈Du,v \in Du,v∈D,使
gcd(a,b)=au+bv.\gcd(a,b) = au + bv.gcd(a,b)=au+bv.
**定义 ** 欧几里得整环
设 DDD 是整环。如果存在映射
ϕ:D−{0}→N∪{0},\phi: D - \{0\} \to \mathbb{N} \cup \{0\},ϕ:D−{0}→N∪{0},
使对任意的 a,b∈D,b≠0a,b \in D, b \neq 0a,b∈D,b=0,存在 q,r∈Dq,r \in Dq,r∈D,使
a=bq+r,a = bq + r,a=bq+r,
其中 r=0r = 0r=0 或 ϕ(r)<ϕ(b)\phi(r) < \phi(b)ϕ(r)<ϕ(b),则称 DDD 为一个欧几里得整环(Euclidean domain),记作 ED。
定义中的映射 ϕ\phiϕ 通常称为欧氏映射。
**定理 ** 4.4.6
设 q1,q2,⋯,qnq_1, q_2, \cdots, q_nq1,q2,⋯,qn 如 (4.4.2) 式,令
p0=1,p_0 = 1,p0=1,
p1=qn,p_1 = q_n,p1=qn,
p2=qn−1p1+1,p_2 = q_{n-1}p_1 + 1,p2=qn−1p1+1,
p3=qn−2p2+p1,p_3 = q_{n-2}p_2 + p_1,p3=qn−2p2+p1,
⋯⋯\cdots \cdots⋯⋯
pn=q1pn−1+pn−2,p_n = q_1p_{n-1} + p_{n-2},pn=q1pn−1+pn−2,
则
u=(−1)n−1pn−1,v=(−1)npn.u = (-1)^{n-1}p_{n-1}, \quad v = (-1)^n p_n.u=(−1)n−1pn−1,v=(−1)npn.
*4.5唯一分解整环上的多形式环
参考:
近世代数 | 韩士安, 林磊 | download on Z-Library近世代数 ——韩士安
代数结构入门:群、环、域、向量空间 - 知乎
【静夜思】一些抽象代数的核心思想和实际应用_抽象代数有什么用-CSDN博客
