【左程云算法020】递归和master公式
文章目录
- 从思想上理解递归
- 从实际上理解递归
- 任何递归函数都一定可以改为非递归
- 递归改为非递归的必要性
- Master公式
- 所有子问题规模相同的递归才能用master公式,T(n) = a*T(n/b)+0(n^c),a\b\c都是常数
- 如果log(b,a) < c,复杂度为:O(n^c)
- 如果log(b,a) > c,复杂度为:O(n^log(b,a))
- 如果log(b,a) == c,复杂度为:O(n^c*logn)
- 一个补充:T(n) = a*T(n/b)+0(n*logn),时间复杂度是O(n*((logn)的平方)),证明过程比较复杂,记住即可
视频链接
【算法讲解020【必备】递归和master公式】

从思想上理解递归
给定一个数组,我想用递归的写法在其中找最大值。
public class Video_020_MaxValue{
return f(arr,0,arr.length-1);
}
//arr[l...r]范围上的最大值
public static int f(int[] arr,int l,int r){
if(l==r){//说明只有一个数了,那最大值就是它本身 也叫base case 就是简单到不能再划分
return arr[l];
}
int m = (l+r)/2;//如果不止一个数,切除中点
int lmax = f(arr,l,m);//左侧的最大值求出来
int rmax = f(arr,m+1,r);//右侧的最大值求出来
return Math.max(lmax,rmax);//整体的最大值就是左边的最大值和右边的最大值求最大
}
public static void main(String[] args){
int [] arr = {3,8,7,6,4,5,1,2};
System.out.println("数组最大值:"+maxValue(arr));}
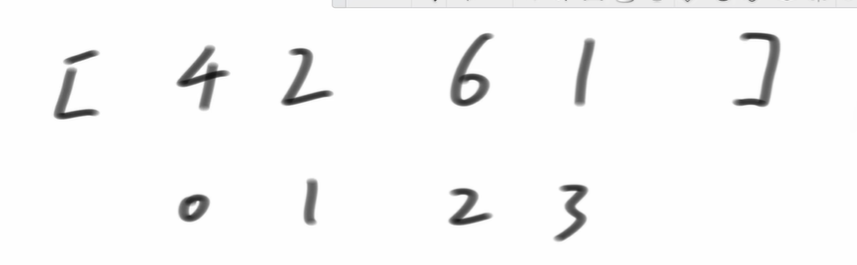
比如求解第0-3位上的最大值
即为求f(0,3)
左边拆解为->f(0,1)
->左边拆解为f(0,0)->最大值是4
->右边拆解为f(1,1)->最大值是2
所以f(0,1)综合左最大值和右最大值,是4
右边拆解为f(2,3)
->左边拆解为f(2,2)->最大值是6
->右边拆解为f(3,3)->最大值是1
所以f(0,1)综合左最大值和右最大值,是6
所以综合最大是6
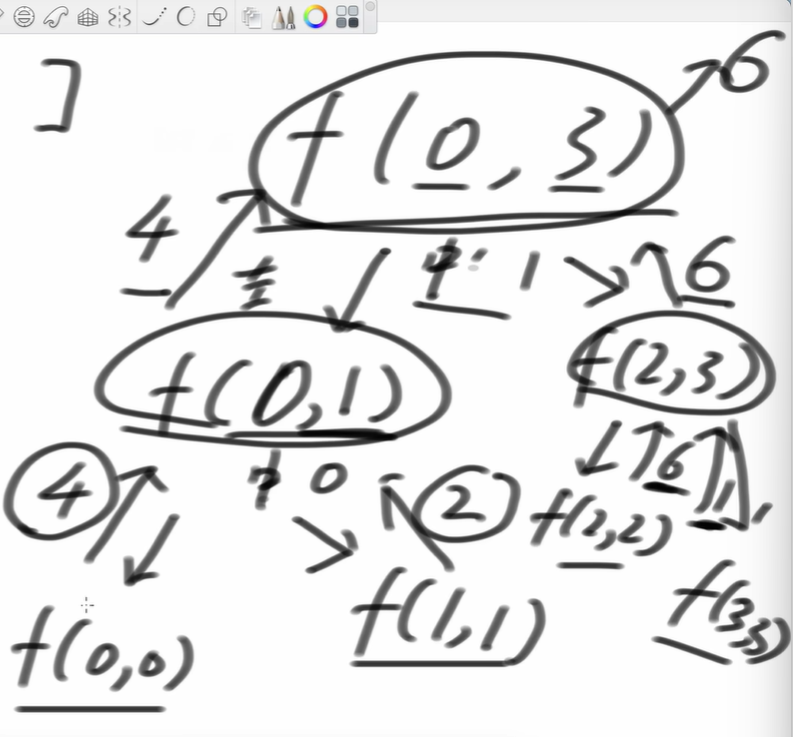
从实际上理解递归
系统再运行递归的时候是在系统栈进行的
f(0,3)没中data base
所以求mid=1
int m = (l+r)/2;
紧接着下一行
int lmax = f(arr,l,m);
我调用了一个新的子过程
系统会把你所有的参数位,临时变量压到栈里面,等着lmax,此时这个函数就销毁了(f(0,3)就销毁了,现在要的是f(0,1))
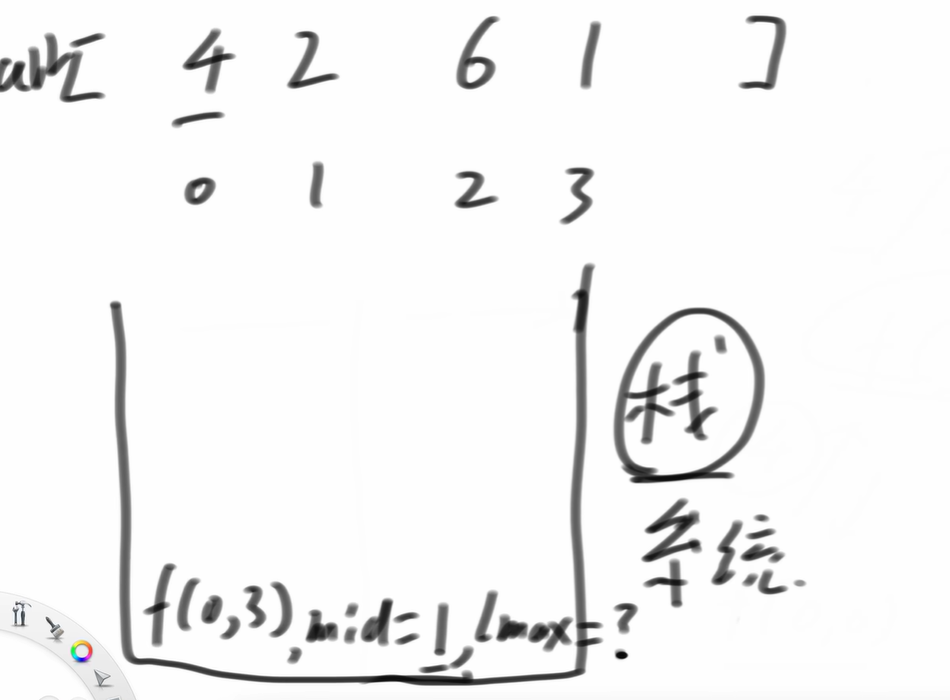
f(0,1)中点是0,现在又跑不下去了
又来到了
int lmax = f(arr,l,m);
所以和上面一样
又把参数位,临时变量压到栈里面并销毁原函数(即f(0,1))
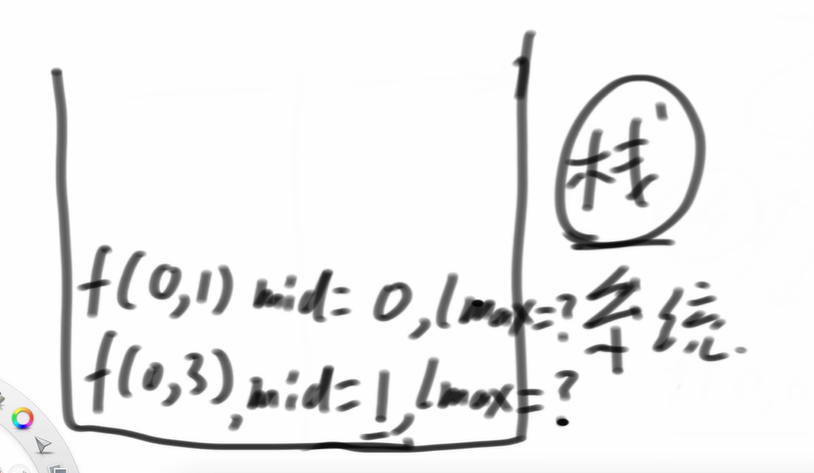
现在就跑f(0,0)
正好指向database,所以说返回4,把这个返回值返回给当前的栈顶
这一行弹出来这个状态

这时候该跑
int rmax = f(arr,m+1,rmax);了
又跑不动
继续压回栈,销毁…
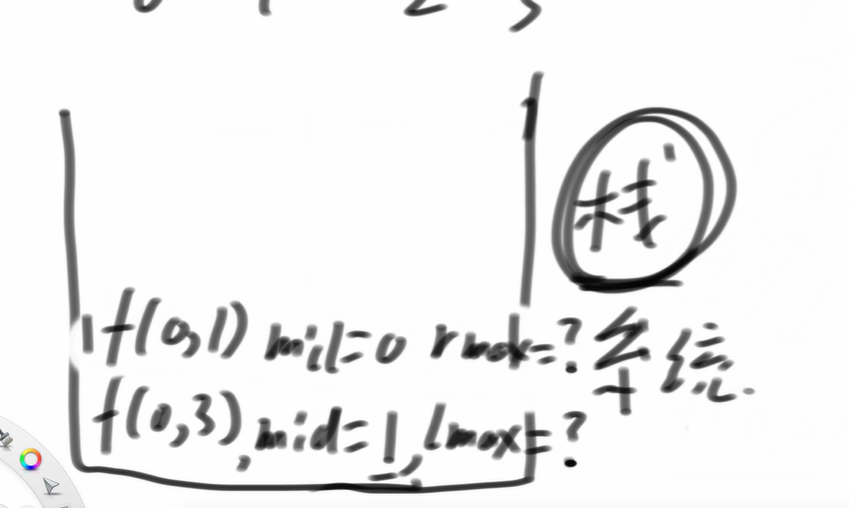
求f(1,1),正好中了data base,将返回值2返回栈顶,状态这一行弹出
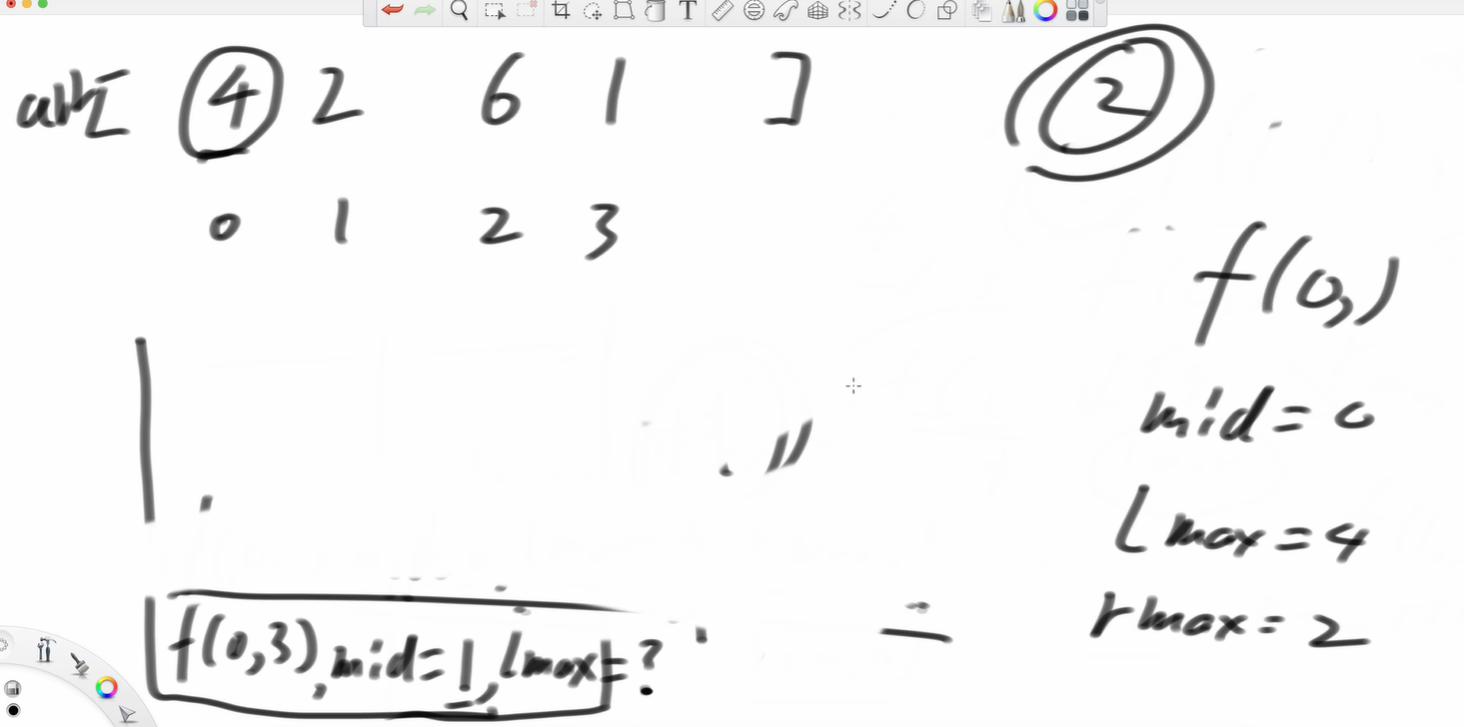
都具备了可以继续往下进行了
return Math.max(lmax,rmax);
返回4给栈顶,又跑不动了
再求rmax
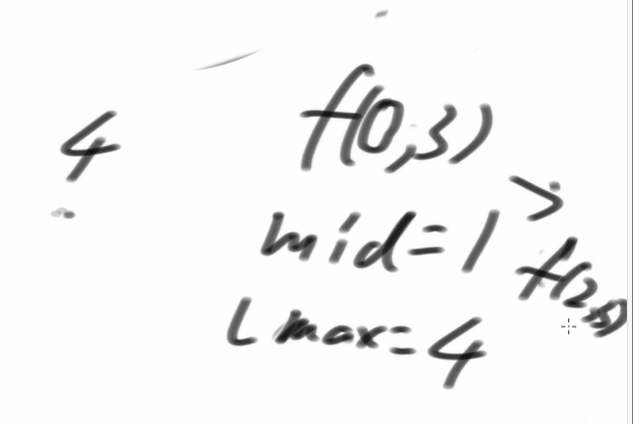
继续压栈,参数位,等rmax
…
总结来说就是一旦它发现它执行不下去了,要等一个什么东西,那这是你的中间变量,参数位等等都会保存在系统栈里,等到算完后给它,它弹出,继续往下进行。
画递归调用图很重要!
任何递归函数都一定可以改为非递归
可以自己做个系统栈
但要注意二者的存储地方不同
系统栈压栈在系统栈空间
自己压栈在内存空间

递归改为非递归的必要性
工程上几乎一定要改
因为系统栈空间很贵,除非确定数据量再大递归层数也一定不深,像归并排序,快速排序,线段树,很多的平衡树等
算法鄙视或者比赛中,能通过就不改
Master公式
所有子问题规模相同的递归才能用master公式,T(n) = a*T(n/b)+0(n^c),a\b\c都是常数
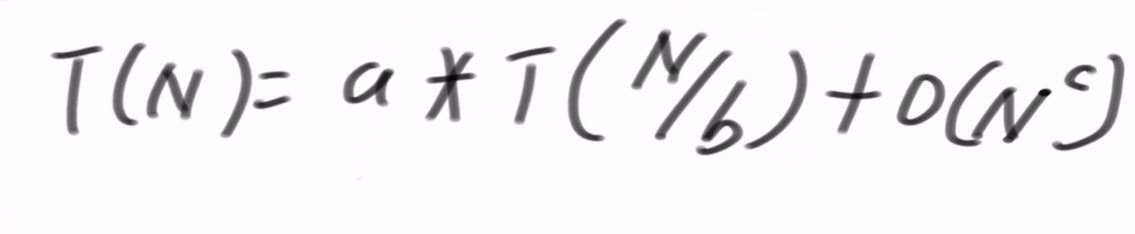
解释一下这个公式
a*T(n/b)
假设现在我要求l到r上的最大值,一共有n个数
我要完成整个任务,我是先调用了左侧一半的数据链,给我了一个最大值。
我又调用了右侧一半的数据链,给我了一个最大值。
对于这个问题来说,b=2,a是子过程调用了几次,左边一次右边一次,所以是两次,即a=2
0(n^c)
除了子过程调用之外,这个代码里其它行为的时间复杂度是多少。
这个问题里其它的都是O(1)的,所以这个通项公式可以写成O(1)
那这道题的公式就是
T(N) = 2*T(N/2)+O(1)
即a = 2(整个子过程调用了几次),
b = 2(调用一次数据量减少了多少),
c =0(剩余过程的时间复杂度)
master公式可以直接告诉你整个过程时间复杂度是多少,结论:
如果log(b,a) < c,复杂度为:O(n^c)
如果log(b,a) > c,复杂度为:O(n^log(b,a))
如果log(b,a) == c,复杂度为:O(n^c*logn)
比如下面的问题,
给你一个数组,我想左边2/3取个最大值,右边2/3取个最大值(所以中间有重合部分),再综合求整个最大值
那么master公式即为:
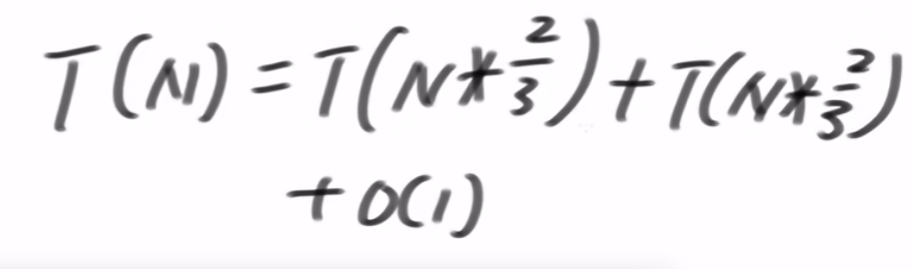
即
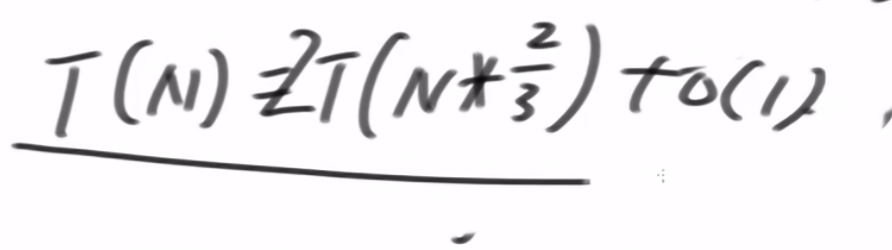
所以得到abc
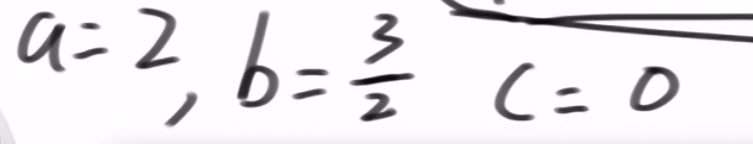
再举个例子
给你一个数组,我想左边1/2取个最大值,右边1/2取个最大值,再把整个数组都遍历打印一遍,最后综合求整个最大值
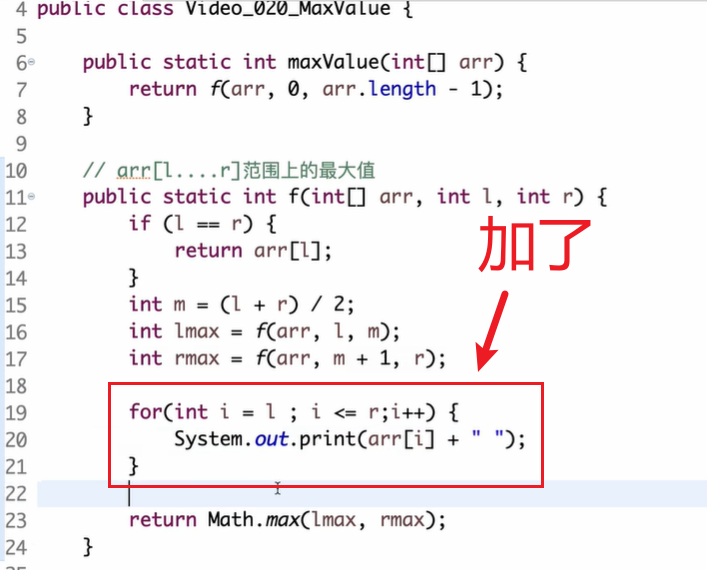
那么此时master公式为:
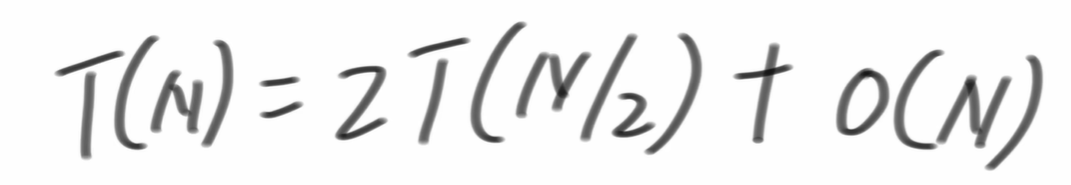
变动的地方就是原来其它复杂度是O(1),加上for循环后复杂度变为O(n)了,其它地方没变
所以abc即为
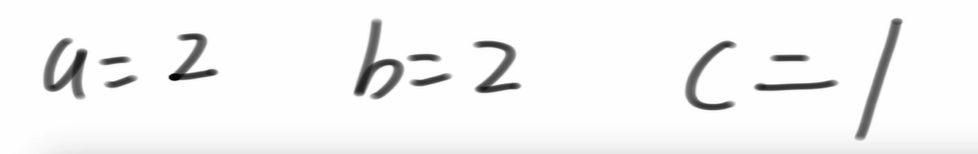
总结
master公式可以应用在子问题规模相同的递归
比如左边1/2求最大,右边1/2求最大
比如左边2/3求最大,右边2/3求最大
但是
左边1/3求最大,右边2/3求最大 不能用master公式
这样你只需要看一层就能知道整个过程的时间复杂度
