【论文阅读】-《Sparse Adversarial Attack via Perturbation Factorization》

通过扰动因子分解进行稀疏对抗攻击

摘要

本文研究稀疏对抗攻击，其目标是在一张良性图像的部分位置上生成对抗性扰动，使得被扰动的图像被某个深度神经网络（DNN）模型错误预测。稀疏对抗攻击涉及两个挑战，即扰动哪些位置以及如何确定扰动幅度。许多现有工作手动或启发式地确定扰动位置，然后使用为密集对抗攻击设计的适当算法来优化扰动幅度。在这项工作中，我们提出将每个像素处的扰动分解为两个变量的乘积，包括扰动幅度和一个二元选择因子（即 $0$ 或 $1$）。如果一个像素的选择因子是 $1$，则该像素被扰动，否则不被扰动。基于这种分解，我们将稀疏攻击问题表述为一个混合整数规划（MIP）问题，以联合优化所有像素的二元选择因子和连续扰动幅度，并对选择因子施加基数约束以显式控制稀疏度。此外，扰动分解提供了额外的灵活性，可以在选择因子或幅度上融入其他有意义的约束，以实现某些期望的性能，例如组稀疏性或增强的视觉不可感知性。我们通过将 MIP 问题等价地重新表述为一个连续优化问题，开发了一种高效的算法。大量实验证明了所提方法相对于几种最先进的稀疏攻击方法的优越性。所提方法的实现可在 https://github.com/wubaoyuan/Sparse-Adversarial-Attack 获取。

关键词： 扰动因子分解，稀疏对抗攻击，混合整数规划

电子补充材料

本章的在线版本 (https://doi.org/10.1007/978-3-030-58542-6_3) 包含补充材料，可供授权用户使用。

1 引言

深度神经网络（DNNs）在许多应用中取得了巨大成功，例如图像分类 [16, 32, 35]、人脸识别 [31, 34]、自然语言处理 [29] 等。然而，研究发现 DNNs 容易受到对抗样本 [2, 15, 33] 的攻击，其中微小的恶意扰动就可能导致 DNNs 做出错误的预测。这在许多基于 DNN 的应用中都有观察到，例如图像分类 [9, 14, 21]、图像描述 [8, 39]、图像检索 [4, 13]、问答 [23]、自动驾驶 [24]、自动结账 [25]、人脸识别 [12]、人脸检测 [22] 等。

大多数现有的对抗攻击方法侧重于优化扰动幅度，使得扰动对人眼不可感知，而扰动位置则未被考虑，因为假设所有像素都会被扰动。这被称为密集对抗攻击。相比之下，最近的一些工作 [7, 17] 观察到，即使只扰动部分位置（甚至图像中的一个像素 [30]），DNN 模型也可能被欺骗，这被称为稀疏对抗攻击。与密集攻击相比，如先前工作 [38] 所分析，稀疏攻击不仅产生的扰动更少，而且为 DNNs 的脆弱性提供了额外的见解，即对抗攻击的更好解释。例如，如图 1 所示，我们的攻击方法生成的稀疏扰动主要发生在良性图像中主要对象的位置上，例如第二张良性图像中“阿拉伯骆驼”的身体区域。扰动位置揭示了图像的哪

图 1： 在从 ImageNet [11] 中选择的两张良性图像上，针对图像分类的目标稀疏对抗攻击的示例。（左）：良性图像，下方是其真实标签。（中）：由 C&W-${\ell }_0$ 攻击 [7] 生成的扰动。（右）：由我们的攻击方法生成的扰动。每个扰动下方的文本分别表示目标攻击类别、扰动的 ${\ell }_0,{\ell }_1,{\ell }_2,{\ell }_{\infty }$-范数。与 C&W-${\ell }_0$ 攻击相比，我们的方法成功地将良性图像攻击到目标类别，且扰动像素更少、失真更低。

部分对于 DNN 模型的预测是重要但脆弱的。尽管有这些优点，稀疏攻击也存在一个额外的挑战，即如何确定扰动位置。一些现有工作（例如 LaVAN [17]）手动确定一个局部块。然后采用为密集攻击设计的攻击算法在该局部块内生成扰动。一些工作尝试使用启发式策略确定扰动位置。例如，C&W-${\ell }_0$ [7] 在每次迭代中逐渐固定一些对分类输出贡献不大的像素。这些启发式方法无法保证能够识别出令人满意的扰动位置。

在这项工作中，我们提供了一个新的视角，即每个像素上的扰动可以根据其两个特征进行分解，即幅度和位置。因此，每个单独的扰动可以表示为扰动幅度和一个二元选择因子（即 0 或 1）之间的乘积。如果选择因子是 1，则相应的像素被扰动，否则不被扰动。这个简单的视角带来了多重好处。首先，稀疏对抗攻击可以被表述为一个混合整数规划（MIP）问题，该问题联合优化图像中所有像素的二元选择因子和连续扰动幅度。并且，通过对所有二元选择因子施加基数约束，可以显式地强制执行被扰动像素的数量。与前述的两阶段方法（例如 [7, 17]）相比，所提出的联合优化有望生成更好的扰动（即更少的扰动位置或更小的扰动幅度），并且能够更方便地控制稀疏度。其次，扰动分解提供了额外的灵活性，可以在扰动幅度或二元选择因子上施加一些有意义的约束，以实现某些期望的攻击性能。我们提出了两个案例研究。一个是对选择因子施加组稀疏性，以鼓励扰动聚集在一起。另一个是根据良性图像的像素值，将每个像素的先验权重引入到扰动幅度上，以增强对人眼视觉感知的不可感知性。这两者都可以自然地嵌入到所提出的联合优化问题中。此外，MIP 问题是 NP 难的，不能直接通过任何现成的连续优化求解器进行优化。受最近一种称为 ${\ell }_p$-Box ADMM [36] 的用于整数规划（IP）的方法的启发，我们提出将 MIP 问题重新表述为一个等价的连续优化问题，然后使用迭代方案高效求解。最后，我们在两个基准数据库上进行了广泛的实验，包括 CIFAR-10 [18] 和 ImageNet [11]，以验证所提方法的性能。

这项工作的主要贡献有四点。1) 我们提供了一个新的视角，即每个像素上的扰动可以分解为扰动幅度和一个二元选择因子的乘积。2) 我们将稀疏对抗攻击表述为一个 MIP 问题，以联合优化扰动幅度和二元选择因子，并对选择因子施加基数约束以精确控制稀疏度。3) 我们开发了一种有效

且高效的连续算法来解决该 MIP 问题。4) 在两个基准数据库上的实验结果表明，所提出的模型优于几种最先进的稀疏攻击方法。

2 相关工作

在本节中，我们关注现有的稀疏对抗攻击工作。与密集对抗攻击相比，稀疏对抗攻击的一个特殊挑战是如何确定扰动位置。根据应对这一挑战的策略，我们将现有的稀疏攻击方法分为三类，包括手动、启发式和优化策略。首先，手动策略意味着攻击者手动指定扰动位置。例如，LaVAN [17] 提出在良性图像上添加一个对抗性但可见的局部块来欺骗基于 CNN 的分类模型。它证明了模型可能被位于背景区域的一个小块（约占图像的 $2\%$）所欺骗。然而，局部块的确切位置是由攻击者手动确定的。其次，在一些工作中，扰动位置是根据一些启发式策略确定的。例如，称为基于雅可比显著性图攻击（JSMA）[28] 的方法及其扩展 [7] 提出根据显著性图确定扰动位置。CornerSearch [10] 利用启发式采样来确定扰动像素。第三，一些工作尝试优化扰动位置。例如，One-Pixel 攻击 [30] 探索了仅攻击一个像素来欺骗 DNN 模型的极端情况。扰动的像素使用差分进化（DE）算法进行搜索。在 [41] 中提出的另一个尝试利用 ${\ell }_0$ 最小化来强制扰动的稀疏性。然后采用交替方向乘子法（ADMM）来分离 ${\ell }_0$-范数和对抗损失，以促进稀疏攻击的优化。然而，对扰动幅度没有约束，导致学习到的扰动可能非常大以至于可见。此外，由于稀疏性是通过目标函数中的 ${\ell }_0$ 项来强制执行的，因此很难精确控制稀疏度。除了像素级稀疏性，[38] 受 Group Lasso [40] 的启发，研究了对抗攻击中的组级稀疏性。他们表明组级稀疏性为对抗攻击提供了更好的可解释性，并证明了学习到的扰动与判别性图像区域高度相关。组级稀疏性可以自然地嵌入到我们的稀疏对抗攻击模型中。

3 稀疏对抗攻击

3.1 对抗攻击预备知识

我们将分类模型表示为 $f:\mathcal{X}\to \mathcal{Y}$，其中 $\mathcal{X}\in [0,1{]}^{w\times h\times c}$ 是图像空间，Y={1,…,K}\mathcal{Y}=\{1,\ldots,K\}Y={1,…,K} 是 $K$ 类输出空间。$\mathbf{x}\in \mathcal{X}$

表示一张良性图像，$ y \in \mathcal{Y} $ 是其真实标签。$ f(x) \in [0,1]^K $ 表示后验向量。对抗攻击通常表述为
$$\underset{ϵ}{\min }\Vert ϵ{\Vert }_p^p+\lambda \mathcal{L}(f(x+ϵ),y_t),\text{ s.t. }x+ϵ\in [0,1],$$
其中损失函数 $\mathcal{L}$ 根据 $y_t$ 指定：如果 $y_t=y$，则称为非目标攻击，$\mathcal{L}$ 设置为负交叉熵函数；如果 $y_t\ne y$ 是攻击指定的另一个目标标签，则称为目标攻击，$\mathcal{L}$ 设置为交叉熵函数。在这项工作中，我们专注于目标攻击，因为它比非目标攻击更具挑战性。$p$ 的值可以根据攻击者的要求指定为不同的值。广泛使用的值包括 $p=2$（例如 C&W-L2 [7]），$p=\infty$（例如 FGSM [33]）。使用这些范数，对抗性扰动可以添加到所有像素上，称为密集攻击。相反，如果 $p=0$，则上述问题将鼓励只有少数像素被扰动，称为稀疏攻击。然而，由于 ${\ell }_0$-范数的不可微性，直接优化上述问题很困难。相反，一些现有工作（例如 [7,17]）提出使用一些启发式策略交替确定扰动位置并优化扰动幅度。相比之下，我们提出联合优化扰动位置和扰动幅度，如下所述。为清晰起见，$x$ 和 $ϵ$ 从张量重塑为向量，即 $x,ϵ\in {\mathbb{R}}^N$，其中 $N=w\cdot h\cdot c$。

3.2 通过扰动因子分解进行稀疏对抗攻击

我们首先将扰动 $ϵ$ 分解如下：
$$ϵ=\delta \odot G,$$
其中 $\delta \in {\mathbb{R}}^N$ 表示扰动幅度向量；G∈{0,1}NG \in \{0,1\}^NG∈{0,1}N 表示扰动位置向量；$\odot$ 表示逐元素乘积。利用这种分解，我们提出了一种新的稀疏对抗攻击公式，如下：
min⁡δ,G∥δ⊙G∥22+λ1L(f(x+δ⊙G),yt),s.t. 1⊤G=k,G∈{0,1}N,\min_{\delta, G} \| \delta \odot G \|_2^2 + \lambda_1 \mathcal{L}(f(x + \delta \odot G), y_t), \text{ s.t. } 1^\top G = k, \quad G \in \{0,1\}^N,δ,Gmin​∥δ⊙G∥22​+λ1​L(f(x+δ⊙G),yt​), s.t. 1⊤G=k,G∈{0,1}N,
其中 ${\lambda }_1>0$ 是一个权衡参数。基数约束 $1^{\top }G=k$ 用于强制只有 $k<N$ 个像素被扰动。注意，范围约束 $x+\delta \odot G$ 在这里被省略了，因为它可以通过裁剪简单地满足。由于 $\delta$ 是连续的，而 $G$ 是整数的，问题 (3) 是一个混合整数规划（MIP）问题。问题 (3) 表示为 SAPF（通过扰动因子分解的稀疏对抗攻击）。

3.3 MIP 问题的连续优化

混合整数规划（MIP）问题具有挑战性，因为它不能直接使用任何现成的连续求解器进行优化。最近，一种

用于整数规划的通用方法称为 ${\ell }_p$-Box ADMM [36] 证明了离散约束空间可以等价地替换为两个连续约束的交集，并且它在许多整数规划任务中显示出非常优越的性能，例如图像分割、匹配、聚类 [5]、MAP 推理 [37]、CNNs 的模型压缩 [20] 等。受此启发，我们提出将 MIP 问题等价地重新表述为一个连续优化问题，然后通过迭代方案高效优化。具体来说，$\mathbf{G}$ 上的二元约束可以替换如下：

G∈{0,1}N⇔G∈Sb∩Sp,\mathbf{G}\in\{0,1\}^{N}\Leftrightarrow\mathbf{G}\in\mathcal{S}_{b}\cap \mathcal{S}_{p},G∈{0,1}N⇔G∈Sb​∩Sp​,
其中 ${\mathcal{S}}_b=[0,1{]}^N$ 是一个盒约束，${\mathcal{S}}_p=\left\{\mathbf{G}:\Vert \mathbf{G}-\frac{1}{2}{\Vert }_2^2=\frac{N}{4}\right\}$ 是一个 ${\ell }_2$-球约束。由于篇幅限制，我们请读者参阅 [36] 了解 (4) 的详细证明。利用 (4)，问题 (3) 被等价地重新表述为
$$\underset{\mathbf{\delta },\mathbf{G},{\mathbf{Y}}_1\in {\mathcal{S}}_b,{\mathbf{Y}}_2\in {\mathcal{S}}_p}{\min }\Vert \mathbf{\delta }\odot \mathbf{G}{\Vert }_2^2+{\lambda }_1\mathcal{L}(f(\mathbf{x}+\mathbf{\delta }\odot \mathbf{G}),y_t)$$
$$\text{s.t. }{1}^{\top }\mathbf{G}=k,\mathbf{G}={\mathbf{Y}}_1,\mathbf{G}={\mathbf{Y}}_2,$$
其中 ${\mathbf{Y}}_1$ 和 ${\mathbf{Y}}_2$ 是两个附加变量，用于分解 $\mathbf{G}$ 上的盒约束和 ${\ell }_2$-球约束。由于 $\mathbf{\delta }$ 和 $\mathbf{G}$ 之间的逐元素乘积，它们应该交替优化。优化的一般结构总结在算法 1 中，其细节如下所示。

步骤 1：给定 $\mathbf{G}$，通过梯度下降更新 $\mathbf{\delta }$。 给定 $\mathbf{G}$，关于 $\mathbf{\delta }$ 的子问题如下：
$$\underset{\mathbf{\delta }}{\min }\Vert \mathbf{\delta }\odot \mathbf{G}{\Vert }_2^2+{\lambda }_1\mathcal{L}(f(\mathbf{x}+\mathbf{\delta }\odot \mathbf{G}),y_t).$$
它与密集对抗攻击的公式非常相似，并且可以通过梯度下降算法求解，如下：
$$\mathbf{\delta }\leftarrow \mathbf{\delta }-{\eta }_{\mathbf{\delta }}\cdot \nabla \mathbf{\delta }=\mathbf{\delta }-{\eta }_{\mathbf{\delta }}\cdot \left[2(\mathbf{\delta }\odot \mathbf{G}\odot \mathbf{G})+{\lambda }_1\frac{\partial \mathcal{L}(f(\mathbf{x}+\mathbf{\delta }\odot \mathbf{G}),y_t)}{\partial \mathbf{\delta }}\right],$$
其中 ${\eta }_{\mathbf{\delta }}>0$，梯度步数将在实验中指定。

步骤 2：给定 $\delta$，使用 ADMM 更新 G。 给定 $\delta$，关于 $(G,Y_1,Y_2)$ 的子问题如下：
$$\underset{G,Y_1\in S_b,Y_2\in S_p}{\min }\Vert \delta \odot G{\Vert }_2^2+{\lambda }_1\mathcal{L}(f(x+\delta \odot G),y_t)$$
$$\text{s.t. }{1}^{T}G=k,G=Y_1,G=Y_2.$$
它可以通过交替方向乘子法（ADMM）算法 [6] 进行优化。具体来说，(8) 的增广拉格朗日函数是
$$L(G,Y_1,Y_2,Z_1,Z_2,z_3)=\Vert \delta \odot G{\Vert }_2^2+{\lambda }_1\mathcal{L}(f(x+\delta \odot G),y_t)+(Z_1{)}^T(G-Y_1)$$
$$+(Z_2{)}^T(G-Y_2)+z_3(1^{T}G-k)+\frac{{\rho }_1}{2}\Vert G-Y_1{\Vert }_2^2+\frac{{\rho }_2}{2}\Vert G-Y_2{\Vert }_2^2$$
$$+\frac{{\rho }_3}{2}(1^{T}G-k{)}^2+h_1(Y_1)+h_2(Y_2),$$
其中 $Z_1\in {\mathbb{R}}^N,Z_2\in {\mathbb{R}}^N,z_3\in \mathbb{R}$ 是对偶变量，$({\rho }_1,{\rho }_2,{\rho }_3)$ 是正惩罚参数。函数 h1(Y1)=I{Y1∈Sb}h_1(Y_1) = \mathbb{I}_{\{Y_1 \in S_b\}}h1​(Y1​)=I{Y1​∈Sb​}​ 和 h2(Y2)=I{Y2∈Sp}h_2(Y_2) = \mathbb{I}_{\{Y_2 \in S_p\}}h2​(Y2​)=I{Y2​∈Sp​}​ 是指示函数，即当 $a$ 为真时 I{a}=0\mathbb{I}_{\{a\}} = 0I{a}​=0，否则 I{a}=+∞\mathbb{I}_{\{a\}} = +\inftyI{a}​=+∞。遵循 ADMM 算法的常规过程，我们迭代更新原始变量和对偶变量，如下所述。

步骤 2.1：更新 $Y_1$。 $Y_1$ 通过以下最小化问题更新，
$$Y_1=\arg \underset{Y_1\in S_b}{\min }\frac{{\rho }_1}{2}\Vert G-Y_1{\Vert }_2^2+(Z_1{)}^T(G-Y_1).$$
其解是通过将 $Y_1$ 的无约束解投影到 $S_b$ 上得到的，即
$$Y_1={\mathcal{P}}_{S_b}(G+\frac{1}{{\rho }_1}{Z}_1),$$
其中 ${\mathcal{P}}_{S_b}(\mathbf{a})=\min (1,\max (0,\mathbf{a}))$，$\mathbf{a}\in {\mathbb{R}}^n$ 表示投影到盒约束 $S_b$ 上。由于 (10) 的目标函数是凸的，并且约束空间 $S_b$ 也是凸的，很容易证明解 (11) 是问题 (10) 的最优解。

步骤 2.2：更新 $Y_2$。 $Y_2$ 通过以下最小化问题更新，
$$Y_2=\arg \underset{Y_2\in S_p}{\min }\frac{{\rho }_2}{2}\Vert G-Y_2{\Vert }_2^2+(Z_2{)}^T(G-Y_2).$$
根据 [36]，$Y_2$ 计算如下：
$$Y_2={\mathcal{P}}_{S_p}(G+\frac{1}{{\rho }_2}{Z}_2),$$
其中 ${\mathcal{P}}_{S_p}(\mathbf{a})=\frac{\sqrt{n}}{2}\frac{\bar{\mathbf{a}}}{\Vert \bar{\mathbf{a}}\Vert }+\frac{1}{2}1$，$\bar{\mathbf{a}}=\mathbf{a}-\frac{1}{2}1$，$\mathbf{a}\in {\mathbb{R}}^n$ 表示投影到 ${\ell }_2$-球约束 $S_p$ 上。在 [36] 中已经证明，解 (13) 是问题 (12) 的最优解。

步骤 2.3：更新 G。 由于 $\mathcal{L}(f(x+\delta \odot G),y_t)$ 中的非线性函数 $f$，获得 G 的闭式解是不可行的。因此，我们通过梯度下降规则更新 G，
$$G\leftarrow G-{\eta }_G\cdot \frac{\partial L}{\partial G},\text{ 其中 }\frac{\partial L}{\partial G}=2(\delta \odot \delta \odot G)+{\lambda }_1\frac{\partial \mathcal{L}(f(x+\delta \odot G),y_t)}{\partial G}+{\rho }_1(G-Y_1)+{\rho }_2(G-Y_2)+(z_3+{\rho }_3(1^{T}G-k))\cdot 1+Z_1+Z_2,$$
其中 ${\eta }_G>0$，梯度步数将在实验中指定。

步骤 2.4：更新 $(Z_1,Z_2,z_3)$。 对偶变量更新如下：
$$Z_1\leftarrow Z_1+{\rho }_1(G-Z_1),Z_2\leftarrow Z_2+{\rho }_2(G-Z_2),z_3\leftarrow z_3+{\rho }_3(1^{T}G-k).$$

备注。 由于关于 $\delta$（即步骤 1）和 $G$（即步骤 2.3）的更新是通过梯度下降不精确求解的，因此算法 1 的理论收敛性无法保证。然而，类似于不精确 ADMM 算法，我们发现算法 1 在我们的实验中总是收敛的。在计算复杂度方面，主要开销是计算 $\frac{\partial \mathcal{L}}{\partial \delta }$（见式 (7)）和 $\frac{\partial \mathcal{L}}{\partial G}$（见式 (14)），其确切成本取决于被攻击的模型 $f$。

3.4 SAPF 的两个扩展

方程 (2) 中 $ϵ$ 的分解提供了额外的灵活性，可以在扰动幅度或选择因子（即扰动位置）上施加不同的约束，以实现攻击者期望的某些性能。这里我们提供两个案例研究，包括组级稀疏性和视觉不可感知性。

组级稀疏性。 模型 (3) 是像素级对抗攻击和稀疏性的自然结合。在稀疏性文献中，组级稀疏性 [3,40] 得到了充分研究，并在鼓励选择分组变量方面显示出有希望的性能。最近一项名为 StrAttack [38] 的工作将组级稀疏性引入对抗攻击，为图像不同区域对对抗攻击的影响提供了一些见解。不失一般性，我们假设输入图像 $\mathbf{x}$ 被分割成 $m$ 个子区域 {xi}i=1m\{x^i\}_{i=1}^m{xi}i=1m​。${\delta }^i$ 和 $G^i$ 分别表示对应于第 $i$ 个区域 $x^i$ 的扰动幅度和选择因子。通过幅度和选择因子的分解，组级稀疏性可以通过最小化 ${\sum }_{i=1}^m\Vert G^i{\Vert }_2$ 来实现，该项被添加到模型 (3) 上，得到
min⁡δ,G∈{0,1}N∥δ⊙G∥22+λ1L(f(x+δ⊙G),yt)+λ2∑i=1m∥Gi∥2,s.t. 1TG=k,\min_{\delta, G \in \{0,1\}^N} \|\delta \odot G\|_2^2 + \lambda_1 \mathcal{L}(f(x + \delta \odot G), y_t) + \lambda_2 \sum_{i=1}^m \|G^i\|_2, \text{ s.t. } 1^T G = k,δ,G∈{0,1}Nmin​∥δ⊙G∥22​+λ1​L(f(x+δ⊙G),yt​)+λ2​i=1∑m​∥Gi∥2​, s.t. 1TG=k,
其中 ${\lambda }_2>0$ 控制组级稀疏性的重要性。这个问题可以使用算法 1 求解，通过修改 $G$ 的更新（见式 (14)），添加 ${\lambda }_2{\sum }_{i=1}^m\Vert G^i{\Vert }_2$ 关于 $G$ 的梯度。这表示为 SAPF-GS。

视觉不可感知性。 视觉不可感知性对于实际的对抗学习很重要。如 [19, 26] 所示，人类对不同图像区域的敏感度根据像素值而变化。因此，将相对较小的扰动分配给具有较高敏感度的区域是有用的。这个策略可以自然地纳入到所提出的模型 (3) 中，如下所示：
min⁡δ,G∥w⊙δ⊙G∥22+λ1L(f(x+δ⊙G),yt),s.t. 1⊤G=k,G∈{0,1}N,\min_{\bm{\delta},\mathbf{G}}\|\bm{w}\odot\bm{\delta}\odot\mathbf{G}\|_{2}^{2}+ \lambda_{1}\mathcal{L}(f(\mathbf{x}+\bm{\delta}\odot\mathbf{G}),y_{t}),\text{ s.t. } \mathbf{1}^{\top}\mathbf{G}=k,\ \mathbf{G}\in\{0,1\}^{N},δ,Gmin​∥w⊙δ⊙G∥22​+λ1​L(f(x+δ⊙G),yt​), s.t. 1⊤G=k, G∈{0,1}N,
其中 $\mathbf{w}\in [0,1{]}^N$ 表示每个像素上预定义的权重。最小化 $\Vert \mathbf{w}\odot \mathbf{\delta }\odot \mathbf{G}{\Vert }_2^2$ 鼓励在权重较高的像素处分配相对较小的扰动，反之亦然。$\mathbf{w}$ 的推导将在实验中讨论。问题 (17) 可以通过稍微修改关于 $\mathbf{\delta }$ 和 $\mathbf{G}$ 的梯度，直接使用算法 1 求解。问题 (17) 表示为 SAPF-VI。

4 实验

在本节中，我们在 CIFAR-10 [18] 和 ImageNet [11] 上进行实验。我们将我们的方法与几种最先进的稀疏对抗攻击算法进行比较，包括五种像素级攻击算法（C&W-${\ell }_0$[7]、One-Pixel-Attack [30]、SparseFool [27]、CornerSearch [10] 和 PGD ${\ell }_0$+${\ell }_{\infty }$[10]），以及一种组级攻击算法（StrAttack [38]）。

4.1 实验设置

数据库和分类模型。 CIFAR-10 有 50k 训练图像和 10k 验证图像，涵盖 10 个类别。遵循 [38]，我们从验证集中随机选择 1,000 张图像作为输入。每张图像除了其真实类别外，还有 9 个目标类别。因此，每种对抗攻击方法总共需要学习 9,000 个对抗样本。ImageNet 包含 1,000 个类别，其中 1.28 百万张图像用于训练，50k 张图像用于验证。我们从验证集中随机选择 100 张覆盖 100 个不同类别的图像。为了降低时间复杂度，我们为 ImageNet 中的每张图像随机选择 9 个目标类别，产生 900 个对抗样本。对于分类模型 $f$，在 CIFAR-10 上，我们遵循 C&W [7] 的设置，训练一个由四个卷积层、三个全连接层和两个最大池化层组成的网络。网络的输入尺寸是 $32\times 32\times 3$。它在验证集上达到了 79.51% 的 top-1 分类准确率。在 ImageNet 上，我们使用一个预训练的 Inception-v3 网络¹ [32]，其 top-1 分类准确率为 77.45%。网络的输入尺寸是 $299\times 299\times 3$。

¹ 从 https://download.pytorch.org/models/inception_v3_google-1a9a5a14.pth 下载。

参数设置。 在所提出的模型 (3) 中，权衡超参数 ${\lambda }_1$ 会影响扰动幅度和攻击成功率。遵循 C&W [7]，我们使用改进的二分搜索来找到合适的 ${\lambda }_1$。具体来说，

在 CIFAR-10 上 ${\lambda }_1$ 初始化为 0.001，在 ImageNet 上初始化为 0.01。${\lambda }_1$ 的下界和上界分别设置为 0 和 100。当生成成功攻击或超过最大搜索次数（例如，我们实验中为 6 次）时，${\lambda }_1$ 的二分搜索停止。此外，在算法 1 中，最大迭代次数设置为 10。在每次迭代期间，G 和 $\mathbf{\delta }$ 都通过梯度下降方法（见式 (7) 和 (14)）更新 2000 步，初始步长为 0.1，并且步长每 50 步衰减一次，衰减率为 0.9。此外，如算法 1 所示，我们采用简单的初始化 $\text{G}=\text{1}$ 和 $\mathbf{\delta }=\text{0}$。它确保了每个单独像素被扰动的公平机会，并避免了由于随机初始化带来的不确定性，使得我们报告的实验结果易于复现。ADMM（见式 (15)）中的超参数 $({\rho }_1,{\rho }_2,{\rho }_3)$ 在 CIFAR-10 和 ImageNet 上初始化为 $(5\times 10^{-3},5\times 10^{-3},10^{-4})$，并在每次迭代后通过 ${\rho }_i\leftarrow$ 1.01$\times {\rho }_i$，$i=1,2,3$ 增加。$({\rho }_1,{\rho }_2,{\rho }_3)$ 的最大值在两个数据库上都设置为 $(20,10,100)$。扰动位置的数量 $k$ 是稀疏攻击的一个关键超参数。在我们的 SAPF 方法中（见模型 (3)），它可以通过基数约束显式控制，而大多数现有稀疏攻击方法则不行。为了确保公平比较，在实验中，我们首先运行达到 100% ASR 的基线 C&W-${\ell }_0$。C&W-${\ell }_0$ 在平均情况下的 ${\ell }_0$-范数作为参考值，用于为其他方法（包括 SAPF）调整 $k$ 值。所有比较方法具有相似水平的稀疏性，便于使用 ${\ell }_2$ 和 ${\ell }_{\infty }$-范数进行比较。

评估指标。 扰动的 ${\ell }_p$-范数（$p=0,1,2,\infty$）和攻击成功率（ASR）用于评估不同方法的攻击性能。在我们的实验中，我们不断增加扰动 ${\ell }_p$-范数的上界，直到攻击成功。换句话说，我们在 100% ASR² 下比较不同攻击算法的扰动 ${\ell }_p$-范数。此外，对于每张图像，类似于 C&W [7]，我们评估三种不同的情况，即平均情况：所有 9 个目标类别的平均性能；最佳情况：所有 9 个目标类别中

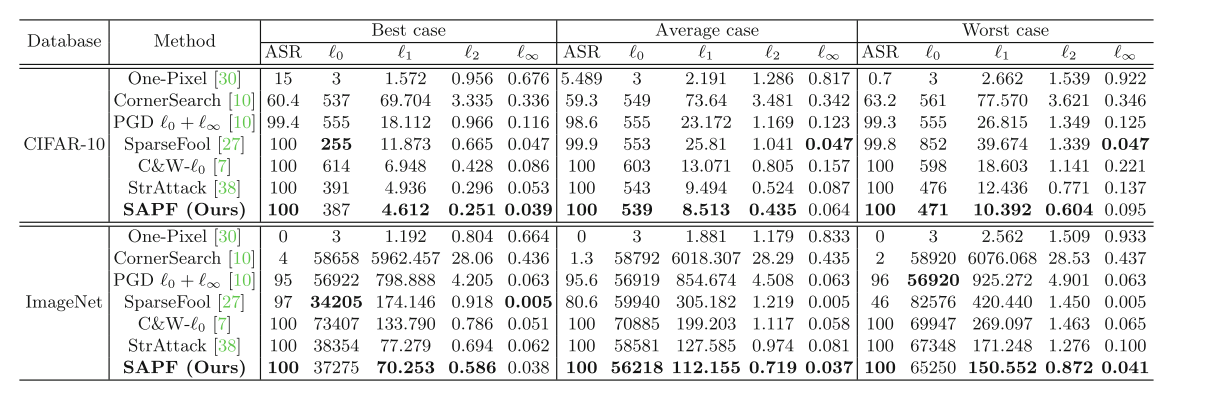
表 1： 在 CIFAR-10 和 ImageNet 上的目标稀疏对抗攻击结果，通过 ASR 和学习到的扰动的 ${\ell }_p$-范数（$p=0,1,2,\infty$）进行评估。在达到超过 90% ASR 的方法中，最好的 ${\ell }_p$-范数以粗体显示。

最容易攻击的目标类别的平均性能；以及最差情况：相对于最难攻击的目标类别的性能。

4.2 SAPF 与其他方法的实验比较

在 CIFAR-10 上的结果。 表 1 给出了在 CIFAR-10 上，三种不同情况下学习到的扰动的平均 ${\ell }_p$-范数和 ASR。从表中我们看到，我们的方法在所有三种情况下都达到了 100% 的攻击成功率。One-Pixel-Attack 的 ${\ell }_{\infty }$-范数是所有算法中最大的，并且它实现了最低的攻击成功率，例如，在最佳情况下它仅达到 15% 的 ASR。因此，即使是在小型数据库 CIFAR-10 上，仅通过扰动一个像素（${\ell }_0=3$ 涉及三个通道）也很难执行目标对抗攻击。CornerSearch 也未能生成 100% 的成功攻击率。与除 One-Pixel-Attack 之外的所有对抗攻击算法相比，我们的方法在所有三种情况下都实现了最好的 ${\ell }_1$-范数和 ${\ell }_2$-范数。这证明了所提方法的有效性。SparseFool 在平均和最差情况下实现了较低的 ${\ell }_{\infty }$-范数。然而，它的 ${\ell }_0$-范数、${\ell }_1$-范数和 ${\ell }_2$-范数显著高于我们的方法。C&W-${\ell }_0$、StrAttack 和我们的方法都达到了 100% 的攻击成功率。然而，通过将扰动分解为位置和幅度并联合优化它们，我们的模型显著优于 C&W-${\ell }_0$ 和 StrAttack，并以最低的 ${\ell }_0$-范数、${\ell }_1$-范数、${\ell }_2$-范数和 ${\ell }_{\infty }$-范数实现了 100% 的 ASR。这些证明了我们提出的方法的优越性。

在 ImageNet 上的结果。 表 1 给出了不同对抗攻击算法在 ImageNet 上的数值结果。从中可见，我们的方法在所有三种情况下都达到了 100% 的攻击成功率。One-Pixel-Attack 和 CornerSearch 算法在所有三种情况下都未能在 ImageNet 上执行目标对抗攻击。SparseFool 方法也未能为许多图像生成成功的

图 2： 所提出的 SAPF 方法生成的扰动示例。（最左列）：来自 ImageNet 的两张良性图像，下方给出了它们的真实类别标签；（第 2 至第 5 列）：生成的具有不同目标攻击类别的稀疏对抗扰动，下方给出了目标攻击类别；（最右列）：四个目标对抗攻击共同的扰动像素。

攻击，特别是在最差情况下，其 ASR 仅为 46%。C&W-${\ell }_0$ 和 StrAttack 算法在所有三种情况下也达到了 100% 的 ASR。然而，我们的方法以最少的扰动位置数实现了相同的 100% ASR。并且 C&W-${\ell }_0$ 和 StrAttack 的 ${\ell }_1$-范数、${\ell }_2$-范数和 ${\ell }_{\infty }$-范数显著高于我们的方法。SparseFool 获得了最低的 ${\ell }_{\infty }$-范数。然而，它未能生成 100% 的 ASR，并且其 ${\ell }_1$-范数和 ${\ell }_2$-范数显著高于我们的方法。

学习到的稀疏扰动的可视化。 稀疏扰动位置在优化过程中自适应地确定。为了更好地理解学习到的扰动位置，我们在图 2 中展示了两个可视化学习到的对抗扰动的示例。图 2 第一列中的良性图像可以被 Inception-v3 模型正确分类。然而，通过在良性图像上添加微小且稀疏的对抗扰动（即从第 2 列到第 5 列的图像），相应的对抗图像成功地欺骗了 Inception-v3 模型。一个有趣的现象是，学习到的扰动位置与判别性图像区域高度相关。例如，在第二行中，当对具有目标攻击类别“Crane”的良性图像“Spider monkey”执行目标攻击时，学习到的稀疏扰动主要位于与对象区域相关的图像区域。在其他图像和不同的目标攻击类别中也可以观察到类似的现象。对于每一行，最右边的图突出显示了在四个不同目标攻击（即第 2 至第 5 列）下总是被扰动的位置。我们观察到，当将某个良性图像攻击到不同的目标类别时，针对不同目标类别的学习到的稀疏扰动共享共同的扰动位置。

稀疏度。 这里我们评估稀疏攻击中不同稀疏度的影响。具体来说，我们使用基数 $k$ 的不同值评估 SAPF（即模型 (3)）。对于每个 $k$，我们不断增加

图 3： 具有组级稀疏性的扰动示例。（左列）：良性图像，下方是其真实类别。（中和右列）分别显示了由 SAPF-GS（即模型 (16)）在 ${\lambda }_2=0$ 和 ${\lambda }_2=10$ 时学习到的扰动。每个扰动下方的文本分别表示其目标攻击类别和 ${\ell }_1,{\ell }_2,{\ell }_{\infty }$-范数。

扰动的幅度，直到攻击成功。图 4 显示了我们的 SAPF 攻击生成的扰动关于扰动位置数 $k$ 的 ${\ell }_p$-范数。随着 $k$ 增加，更多的位置被扰动，并且大多数扰动的幅度减小，导致 ${\ell }_{\infty }$-范数减小。此外，由于每个单独扰动的幅度远小于 1，${\ell }_2$-范数也减小；相反，${\ell }_1$-范数增加，因为新扰动带来的增加大于旧扰动的减少。

4.3 组级稀疏性和视觉不可感知性的结果

具有组级稀疏性的 SAPF。 图 3 分别在中列和右列可视化了没有和有组级稀疏性时学习到的扰动。扰动位置的数量（即 $k$）在这两种情况下是相同的。对于组级稀疏性，我们通过超像素分割 [1] 将输入图像分割成 350 个子区域。比较中列和右列学习到的扰动，具有组级约束的学习到的扰动（即右列中的图）更加集中并聚集在判别性对象区域周围。这有助于探索对对抗攻击敏感的区域。同时，具有组级稀疏性的扰动变得更大（参见图 3 中每个扰动下方的 ${\ell }_p$-范数），但由于目标函数 (16) 中组级稀疏性与其他两项之间的权衡，仍然不可感知。这种权衡在实践中可以通过超参数 ${\lambda }_2$ 在 (16) 中灵活调整。

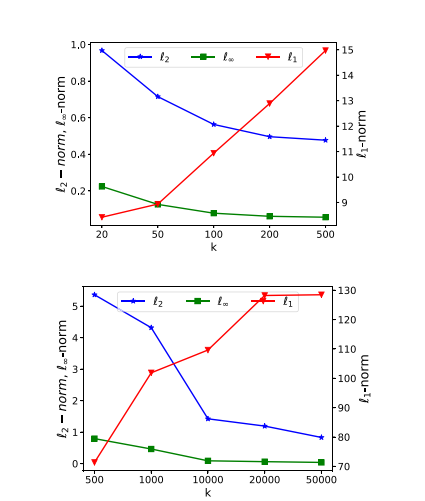
图 4： 在 CIFAR-10（上）和 ImageNet（下）上，由 SAPF 生成的扰动的 ${\ell }_1,{\ell }_2,{\ell }_{\infty }$-范数关于扰动位置数 $k$ 的关系。

图 5： SAPF-VI（即模型 (17)）中不同加权策略的扰动可视化。左上图像是类别为“conch”的良性图像。其他三张图像是使用三种加权策略学习到的扰动位置。目标攻击类别是“fountain”。

具有视觉不可感知性的 SAPF。 对于视觉不可感知性，我们在图 5 中展示了模型 (17) 使用不同加权策略学习到的扰动位置。我们考虑了三种加权策略：“uniform”为每个位置分配相等的权重；“variance”权重 ${\mathbf{w}}_i=1/var({\mathbf{x}}_i)$ [26]，其中 $var({\mathbf{x}}_i)=\sqrt{{\sum }_{{\mathbf{x}}_j\in S_i}({\mathbf{x}}_j-{\mu }_i{)}^2/n^2}$，$S_i$ 表示位置 $i$ 的 $n\times n$ 邻域，${\mu }_i={\sum }_{{\mathbf{x}}_j\in S_i}{\mathbf{x}}_j/n^2$；以及“variance-mean”权重 ${\mathbf{w}}_i=1/(var({\mathbf{x}}_i)\times {\mu }_i)$，$n$ 根据经验设置为 3。为了更好地可视化，我们突出显示了具有最大幅度的前 1% 的扰动位置。“uniform”权重平等对待每个位置，其学习到的扰动位置可能位于人类更敏感的均匀背景区域（例如，图 5 (b) 中的红色框区域）。考虑到人类对较低方差区域的扰动更敏感，“variance”权重鼓励模型将较少的扰动分配给具有较低方差的位置。其学习到的扰动位置主要集中在对具有较高方差的对象区域。“variance-mean”权重进一步考虑了每个位置周围的亮度，其学习到的扰动位置几乎不位于具有较低方差和较低亮度的均匀背景区域。因此，模型 (17) 中的像素权重 $\mathbf{w}$ 会影响学习到的扰动位置，探索不同的加权策略以进一步增强视觉不可感知性是很有趣的。

4.4 补充材料

由于篇幅限制，一些重要内容必须在补充材料中呈现，包括：1) 在 CIFAR-10 上攻击经过对抗训练的模型的结果；2) 不同攻击方法的运行时间；3) 对三个重要问题的详细讨论，包括稀疏对抗攻击的价值、这项工作的最重要贡献以及所提方法的其他扩展。

5 结论

这项工作提供了一个关于对抗性扰动的新视角，即每个扰动可以通过两个特征进行分解，即幅度和位置。这个新视角使得能够将稀疏对抗攻击表述为一个混合整数规划（MIP）问题，该问题联合优化扰动幅度和扰动位置。稀疏度通过扰动位置上的基数约束显式控制。我们通过将 MIP 问题等价地重新表述为一个连续优化问题，开发了一种高效且有效的优化算法。在两个基准数据库上的实验评估证明了所提方法相对于最先进的稀疏对抗攻击方法的优越性。此外，我们可视化了学习到的稀疏位置与判别性区域密切相关，并且还表明所提出的模型可以灵活地纳入对扰动幅度或扰动位置的不同约束，例如组级稀疏性和视觉不可感知性。

致谢

这项工作得到了腾讯 AI Lab 的支持。Yujiu Yang 的参与得到了国家自然科学基金重点项目（批准号：U1903213）的支持。

参考文献

[1] Achanta, R., Shaji, A., Smith, K., Lucchi, A., Fua, P., Susstrunk, S.: Slic superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 34(11), 2274–2282 (2012)

[2] Akhtar, N., Mian, A.: Threat of adversarial attacks on deep learning in computer vision: a survey. IEEE Access 6, 14410–14430 (2018)

[3] Bach, F., Jenatton, R., Mairal, J., Obozinski, G., et al.: Optimization with sparsity-inducing penalties. Found. Trends® Mach. Learn. 4(1), 1–106 (2012)

[4] Bai, J., et al.: Targeted attack for deep hashing based retrieval. In: ECCV (2020)

[5] Bibi, A., Wu, B., Ghanem, B.: Constrained k-means with general pairwise and cardinality constraints. arXiv preprint arXiv:1907.10410 (2019)

[6] Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J., et al.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 3(1), 1–122 (2011)

[7] Carlini, N., Wagner, D.: Towards evaluating the robustness of neural networks. In: 2017 IEEE Symposium on Security and Privacy (SP), pp. 39–57. IEEE (2017)

[8] Chen, H., Zhang, H., Chen, P.Y., Yi, J., Hsieh, C.J.: Show-and-fool: crafting adversarial examples for neural image captioning. arXiv preprint arXiv:1712.02051 (2017)

[9] Chen, W., Zhang, Z., Hu, X., Wu, B.: Boosting decision-based black-box adversarial attacks with random sign flip. In: Proceedings of the European Conference on Computer Vision (2020)

[10] Croce, F., Hein, M.: Sparse and imperceivable adversarial attacks. In: ICCV, pp. 4724–4732 (2019)

[11] Deng, J., Dong, W., Socher, R., Li, L.J., Li, K., Fei-Fei, L.: ImageNet: a large-scale hierarchical image database. In: CVPR, pp. 248–255. IEEE (2009)

[12] Dong, Y., et al.: Efficient decision-based black-box adversarial attacks on face recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 7714–7722 (2019)

[13] Feng, Y., Chen, B., Dai, T., Xia, S.: Adversarial attack on deep product quantization network for image retrieval. In: AAAI (2020)

[14] Feng, Y., Wu, B., Fan, Y., Li, Z., Xia, S.: Efficient black-box adversarial attack guided by the distribution of adversarial perturbations. arXiv preprint arXiv:2006.08538 (2020)

[15] Goodfellow, I.J., Shlens, J., Szegedy, C.: Explaining and harnessing adversarial examples. In: ICLR (2015)

[16] He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: CVPR, pp. 770–778 (2016)

[17] Karmon, D., Zoran, D., Goldberg, Y.: LaVAN: localized and visible adversarial noise. In: ICML (2018)

[18] Krizhevsky, A., Hinton, G.: Learning multiple layers of features from tiny images. Technical report, Citeseer (2009)

[19] Legge, G.E., Foley, J.M.: Contrast masking in human vision. JOSA 70(12), 1458–1471 (1980)

[20] Li, T., Wu, B., Yang, Y., Fan, Y., Zhang, Y., Liu, W.: Compressing convolutional neural networks via factorized convolutional filters. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3977–3986 (2019)

[21] Li, Y., et al.: Toward adversarial robustness via semi-supervised robust training. arXiv preprint arXiv:2003.06974 (2020)

[22] Li, Y., Yang, X., Wu, B., Lyu, S.: Hiding faces in plain sight: Disrupting AI face synthesis with adversarial perturbations. arXiv preprint arXiv:1906.09288 (2019)

[23] Liu, A., et al.: Spatiotemporal attacks for embodied agents. In: European Conference on Computer Vision (2020)

[24] Liu, A., et al.: Perceptual-sensitive GAN for generating adversarial patches. In: 33rd AAAI Conference on Artificial Intelligence (2019)

[25] Liu, A., Wang, J., Liu, X., Cao, b., Zhang, C., Yu, H.: Bias-based universal adversarial patch attack for automatic check-out. In: European Conference on Computer Vision (2020)

[26] Luo, B., Liu, Y., Wei, L., Xu, Q.: Towards imperceptible and robust adversarial example attacks against neural networks. In: AAAI (2018)

[27] Modas, A., Moosavi-Dezfooli, S.M., Frossard, P.: Sparsefool: a few pixels make a big difference. In: CVPR, pp. 9087–9096 (2019)

[28] Papernot, N., McDaniel, P., Jha, S., Fredrikson, M., Celik, Z.B., Swami, A.: The limitations of deep learning in adversarial settings. In: 2016 IEEE European Symposium on Security and Privacy (EuroS&P), pp. 372–387. IEEE (2016)

[29] Sarikaya, R., Hinton, G.E., Deoras, A.: Application of deep belief networks for natural language understanding. IEEE/ACM Trans. Audio Speech Lang. Process. (TASLP) 22(4), 778–784 (2014)

[30] Su, J., Vargas, D.V., Sakurai, K.: One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 23, 828–841 (2019)

[31] Sun, Y., Liang, D., Wang, X., Tang, X.: DeepID3: face recognition with very deep neural networks. arXiv preprint arXiv:1502.00873 (2015)

[32] Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., Wojna, Z.: Rethinking the inception architecture for computer vision. In: CVPR, pp. 2818–2826 (2016)

[33] Szegedy, C., et al.: Intriguing properties of neural networks. In: ICLR (2014)

[34] Wang, H., et al.: CosFace: large margin cosine loss for deep face recognition. In: CVPR, pp. 5265–5274 (2018)

[35] Wu, B., et al.: Tencent ML-images: a large-scale multi-label image database for visual representation learning. IEEE Access 7, 172683–172693 (2019)

[36] Wu, B., Ghanem, B.: $l_p$-box ADMM: a versatile framework for integer programming. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 41, 1695–1708 (2018)

[37] Wu, B., Shen, L., Zhang, T., Ghanem, B.: Map inference via $l_2$-sphere linear program reformulation. Int. J. Comput. Vis. 128, 1–24 (2020)

[38] Xu, K., et al.: Structured adversarial attack: Towards general implementation and better interpretability. In: ICLR (2019)

[39] Xu, Y., et al.: Exact adversarial attack to image captioning via structured output learning with latent variables. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4135–4144 (2019)

[40] Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. J. R. Stat. Soc.: Ser. B (Stat. Methodol.) 68(1), 49–67 (2006)

[41] Zhao, P., Liu, S., Wang, Y., Lin, X.: An ADMM-based universal framework for adversarial attacks on deep neural networks. In: 2018 ACMMM, pp. 1065–1073. ACM (2018)