动规:两个数组dp系列
目录
No.1 最长公共子序列
No.2 不相交的线
No.3 不同的子序列
No.4* 通配符匹配
No.5* 正则表达式匹配
No.6* 交错字符串
No.7 两个字符串的最小ASCII删除和
No.8 最长重复子数组
No.1 最长公共子序列
1143. 最长公共子序列 - 力扣(LeetCode)


涉及两个s的值进行比对,遍历两边元素是否相等,区间扩展同时实现递推,那么可以i,j表示0~i/j区间内的所有子序列,公共子序列的长度(0~i/j是因为要求的是子序列,因为涉及两个数组的比对,所以创建二维dp表)

先依据这个状态表示,根据情况讨论
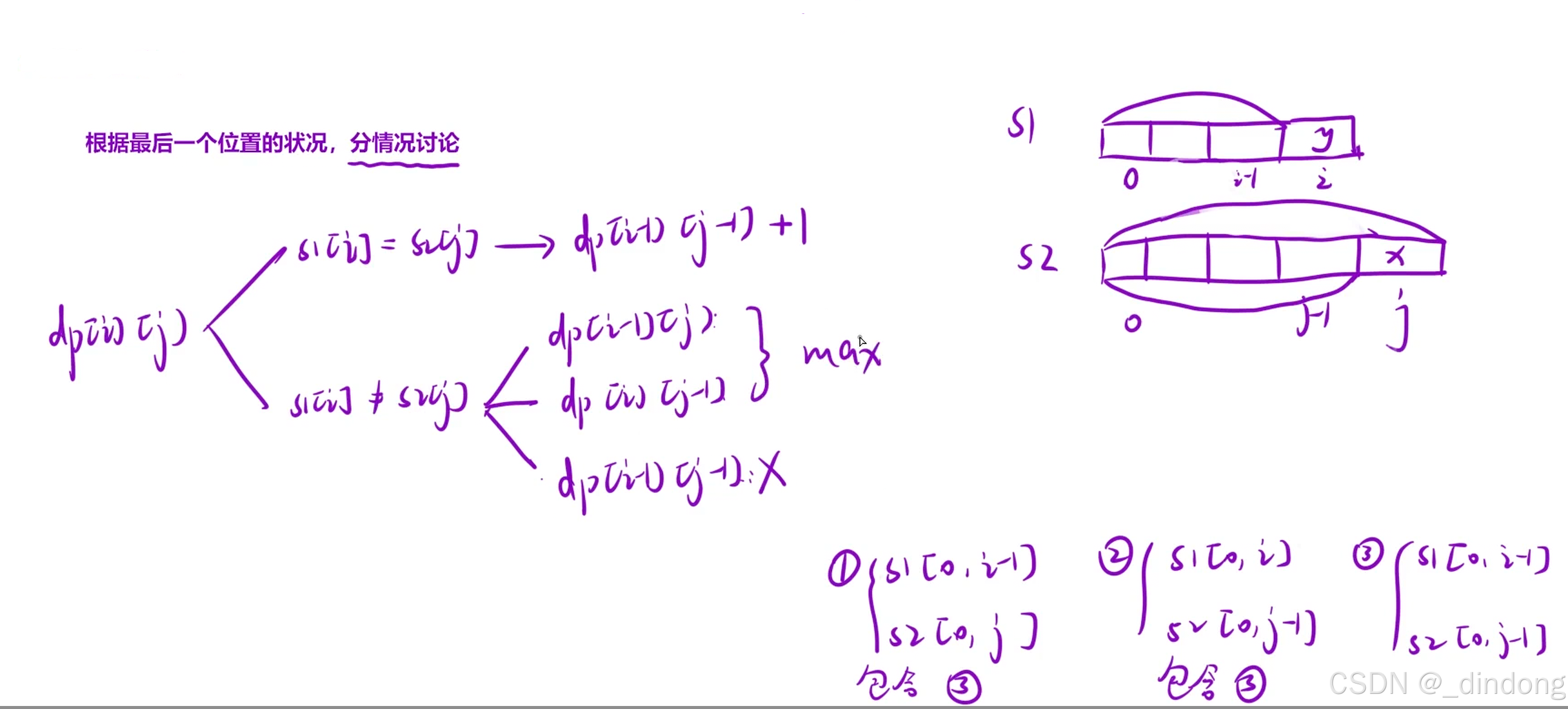
可行
多创建一行一列方便填表
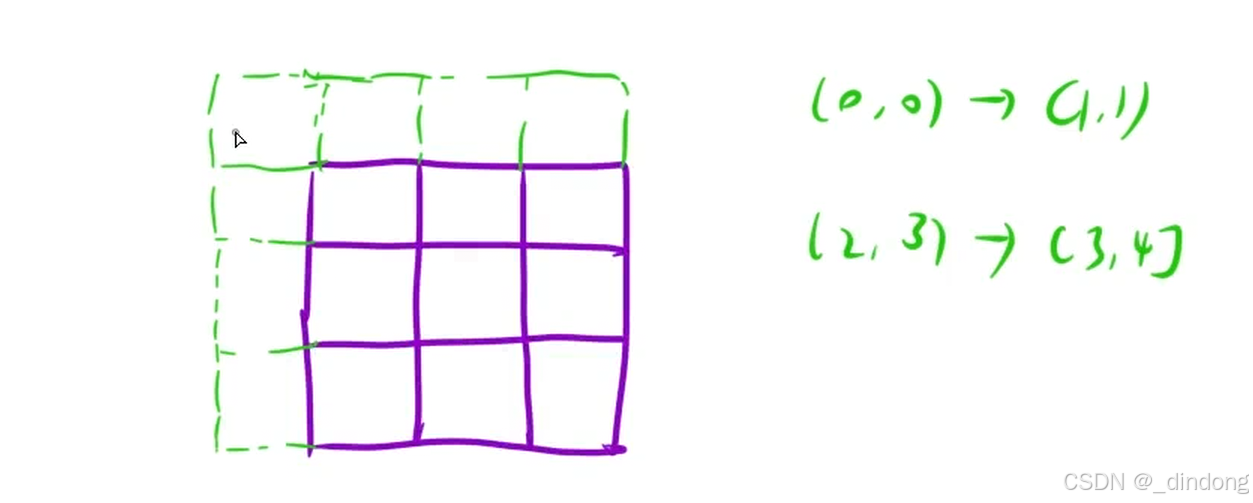
这些位置初始值为0,注意下标映射关系。
ps:在字符串中我们可以采用s='-'+s;的方式将原字符串整体后移一位,这样我们就不必担心映射错误了。
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m=text1.size(),n=text2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(text1[i-1]==text2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
};No.2 不相交的线
1035. 不相交的线 - 力扣(LeetCode)

看明白后就是在求最长公共子序列
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int m=nums1.size(),n=nums2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
};No.3 不同的子序列
115. 不同的子序列 - 力扣(LeetCode)

因为t是需要连续的,要在s里找子序列的个数

那么依旧是对于s的子序列的最后一个位置展开讨论,考虑包不包括最后的这个位置
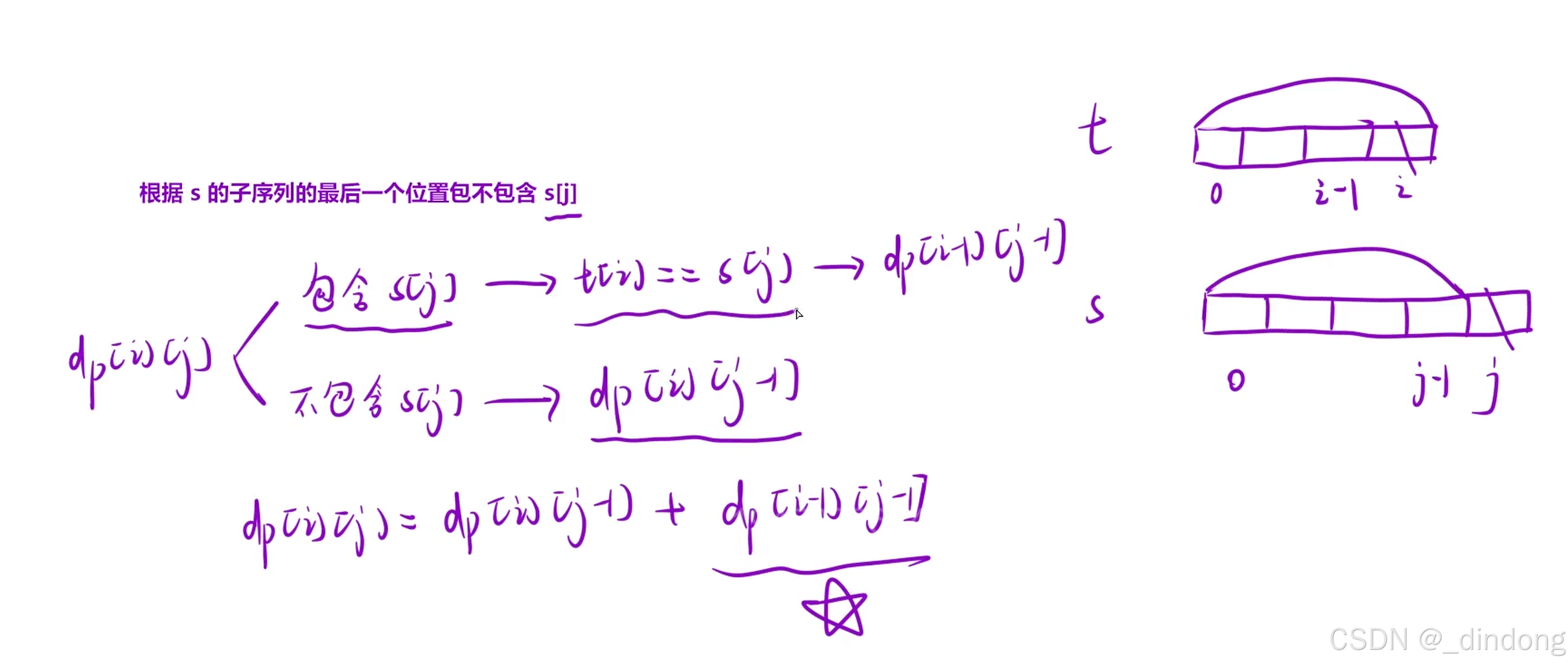
t可以是空串,所以起码有一个结果,创建出的虚拟边界第一行表示t是空串,初始化为1,第一列表示s是空串,除去第一格初始化为0
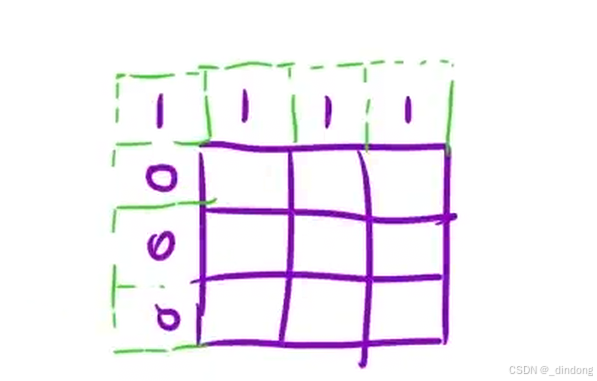
注意下标映射关系
class Solution {
public:int numDistinct(string s, string t) {int m=t.size(),n=s.size();vector<vector<double>> dp(m+1,vector<double>(n+1));for(int j=0;j<=n;++j)dp[0][j]=1;//用t子串的每一个位置去试s的子序列for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){dp[i][j]+=dp[i][j-1];if(t[i-1]==s[j-1])dp[i][j]+=dp[i-1][j-1];}}return dp[m][n];}
};No.4* 通配符匹配
44. 通配符匹配 - 力扣(LeetCode)



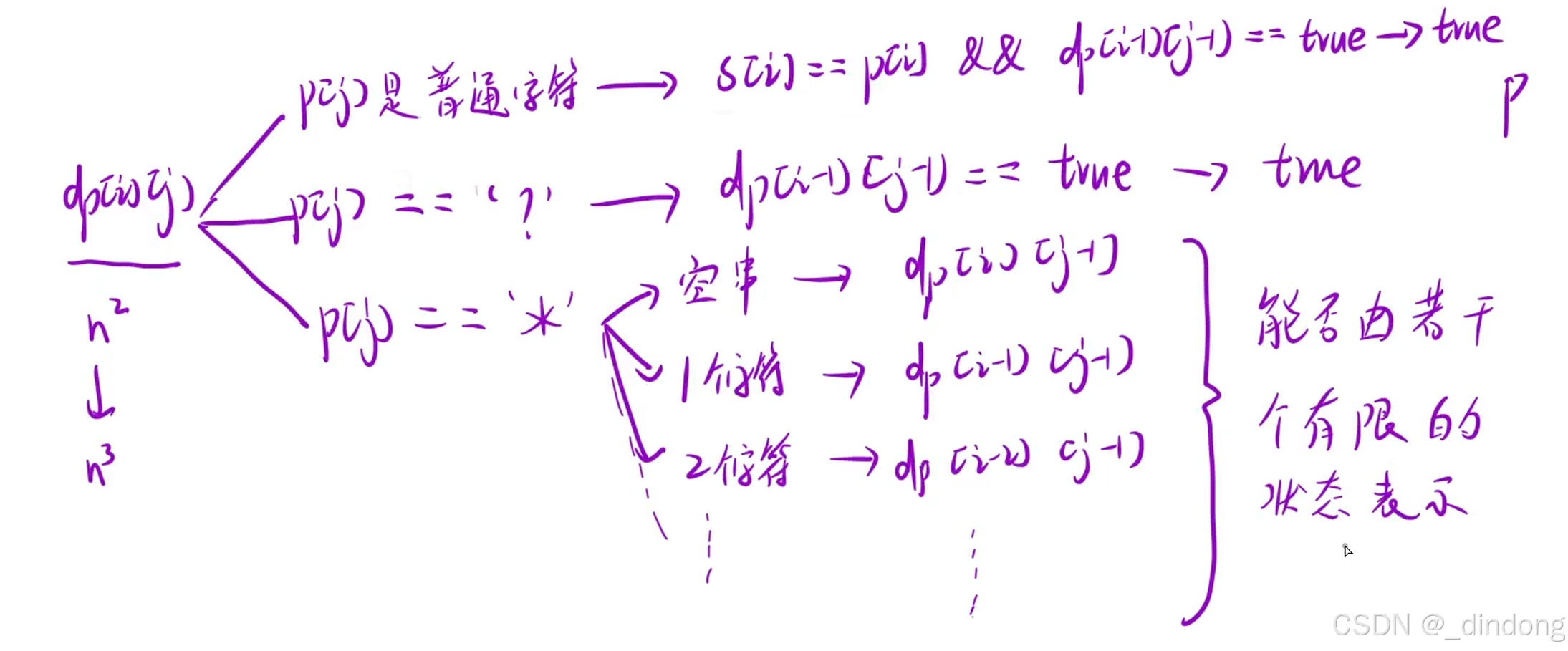
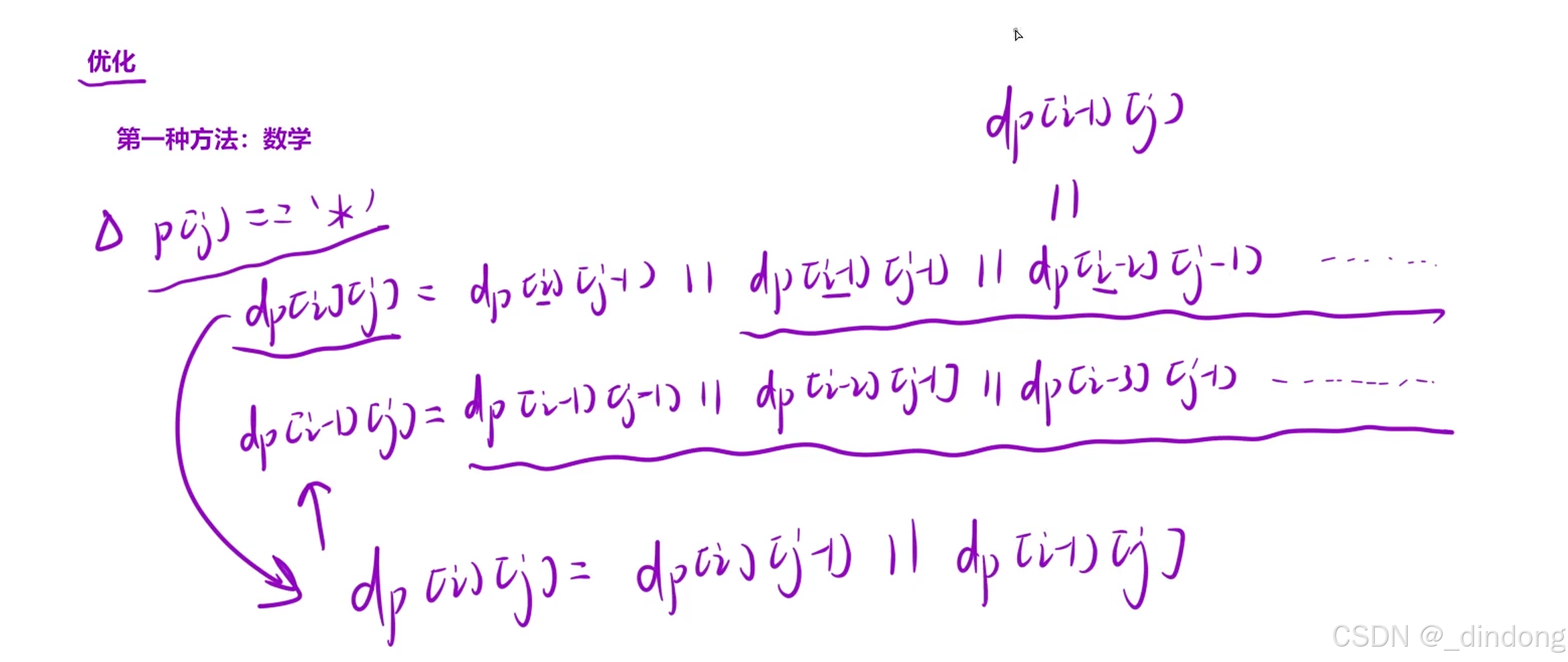

两个其实是一个意思
多创建一行一列,第一行表示s是空,第一列表示p是空
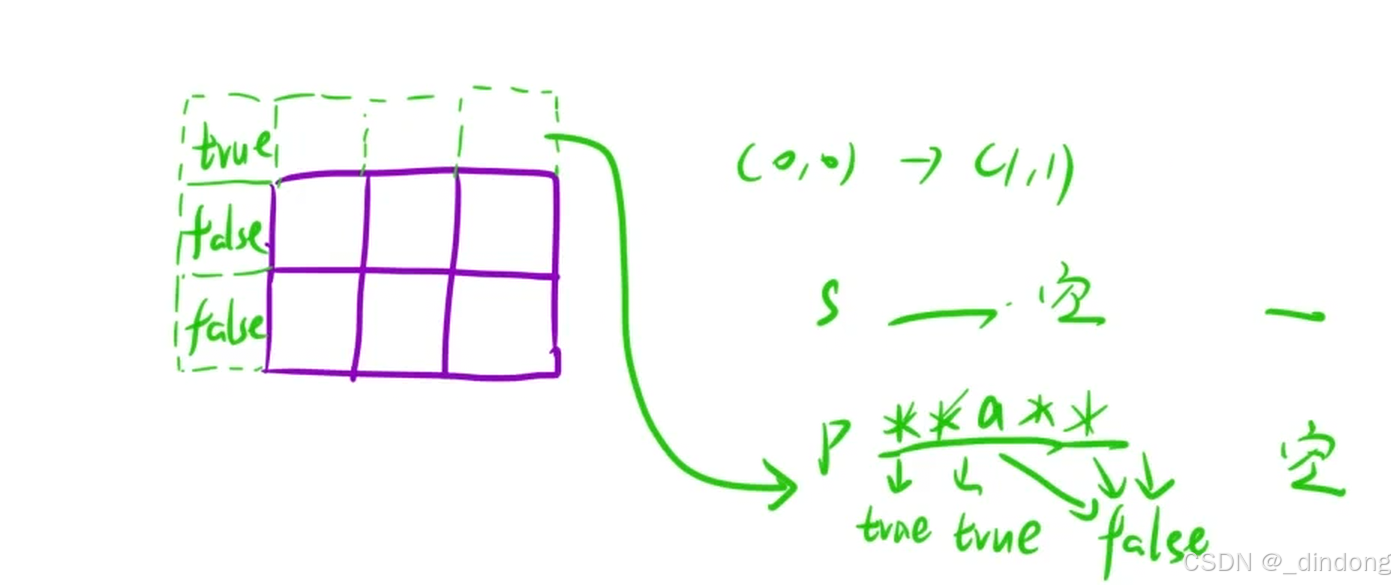
注意下标映射关系
class Solution {
public:bool isMatch(string s, string p) {//准备工作int m=s.size(),n=p.size();vector<vector<bool>> dp(m+1,vector<bool>(n+1));s=" "+s,p=" "+p;//初始化dp[0][0]=true;for(int j=1;j<=n;++j){if(p[j]=='*')dp[0][j]=true;else break;}//填表for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(p[j]=='*'){dp[i][j]=dp[i][j-1]||dp[i-1][j];}else{dp[i][j]=(p[j]=='?'||s[i]==p[j])&&dp[i-1][j-1];}}}return dp[m][n]; }
};No.5* 正则表达式匹配
10. 正则表达式匹配 - 力扣(LeetCode)


这题和前一题的区别在于,*得和前面一个字符搭配使用,表示可以匹配零个或者前面那个字符。


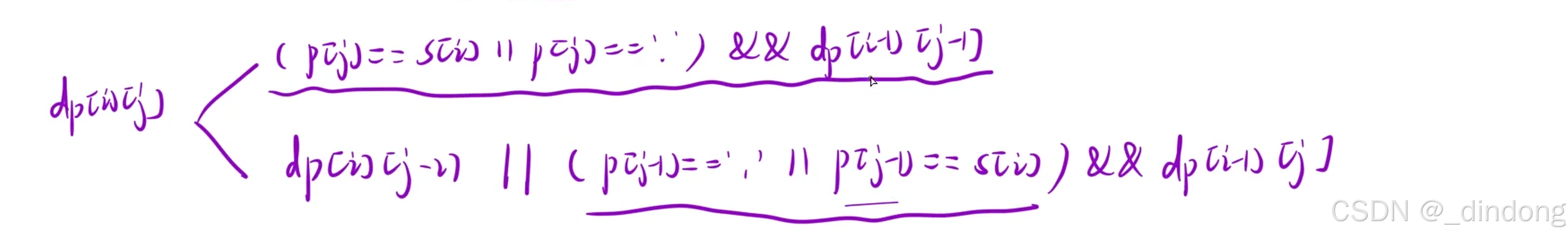
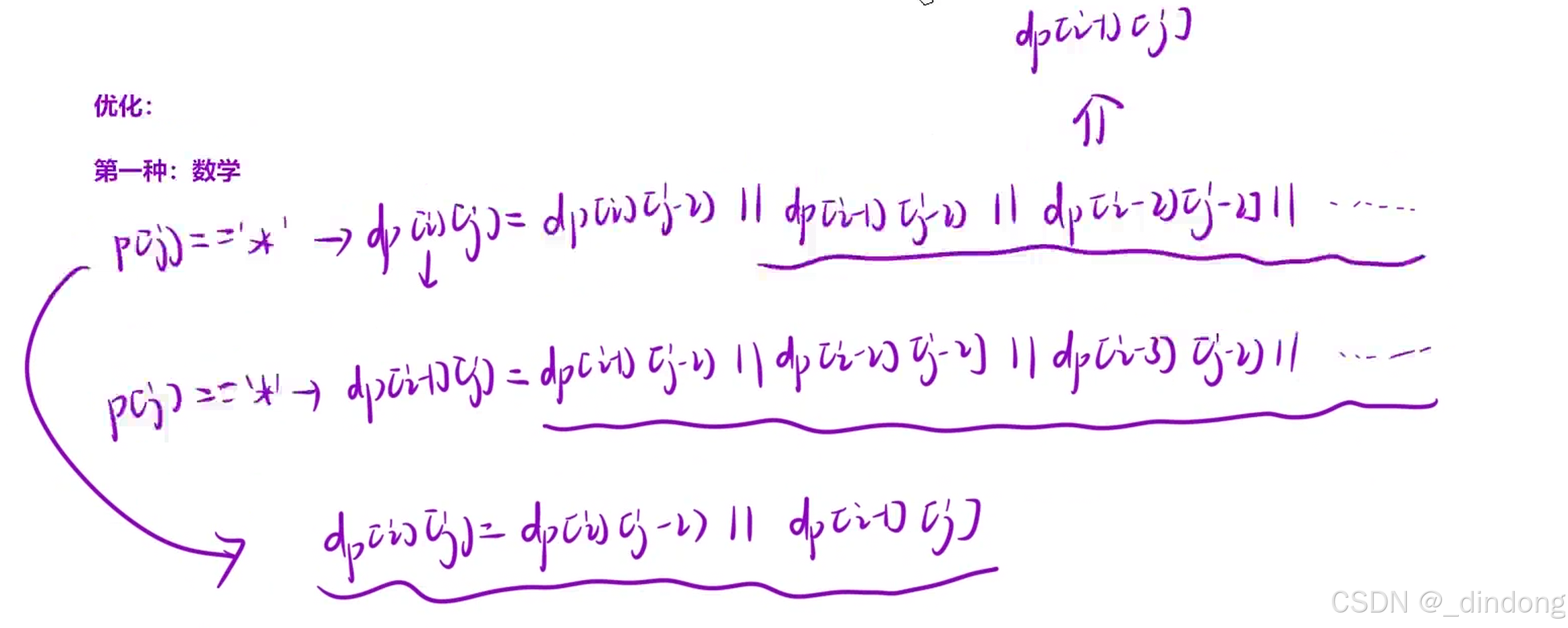

初始化:多创建一行一列,第一行表示s是空,第一列表示p是空
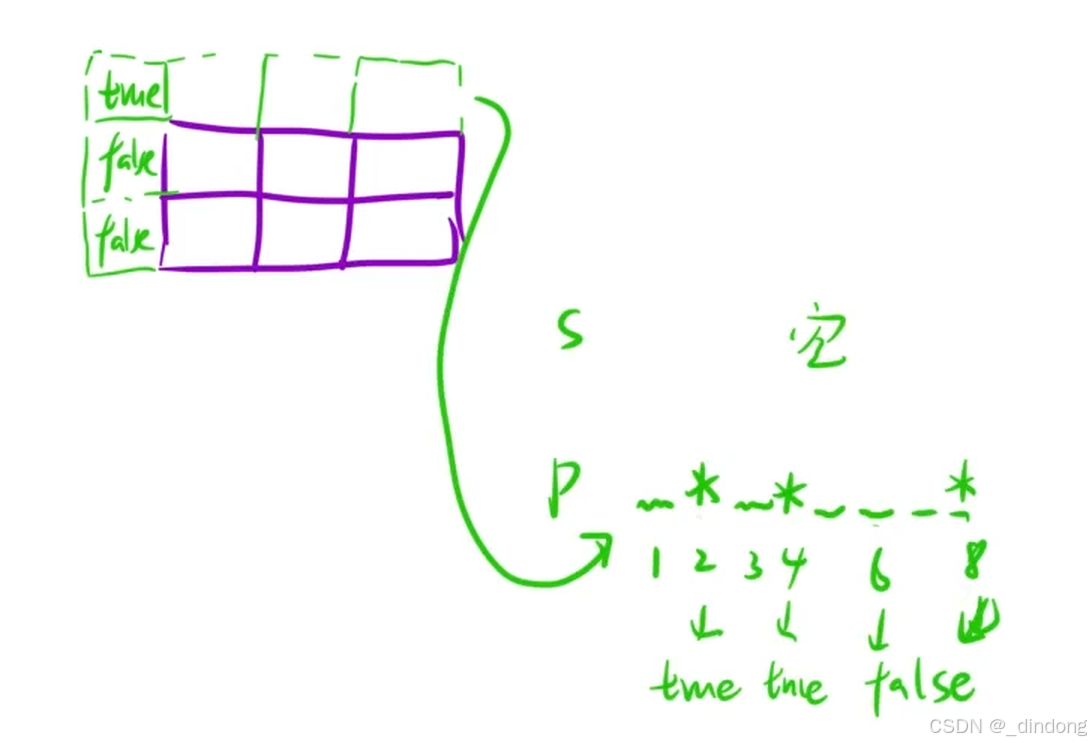
class Solution {
public:bool isMatch(string s, string p) {// 准备工作int m = s.size(), n = p.size();vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));s = " " + s, p = " " + p;// 初始化dp[0][0] = true;for (int j = 2; j <= n; j += 2) {if (p[j] == '*')dp[0][j] = true;elsebreak;}// 填表for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (p[j] == '*') {dp[i][j] =dp[i][j - 2] ||((p[j - 1] == '.' || p[j - 1] == s[i]) && dp[i - 1][j]);} else {dp[i][j] =(p[j] == '.' || s[i] == p[j]) && dp[i - 1][j - 1];}}}return dp[m][n];}
};No.6* 交错字符串
97. 交错字符串 - 力扣(LeetCode)
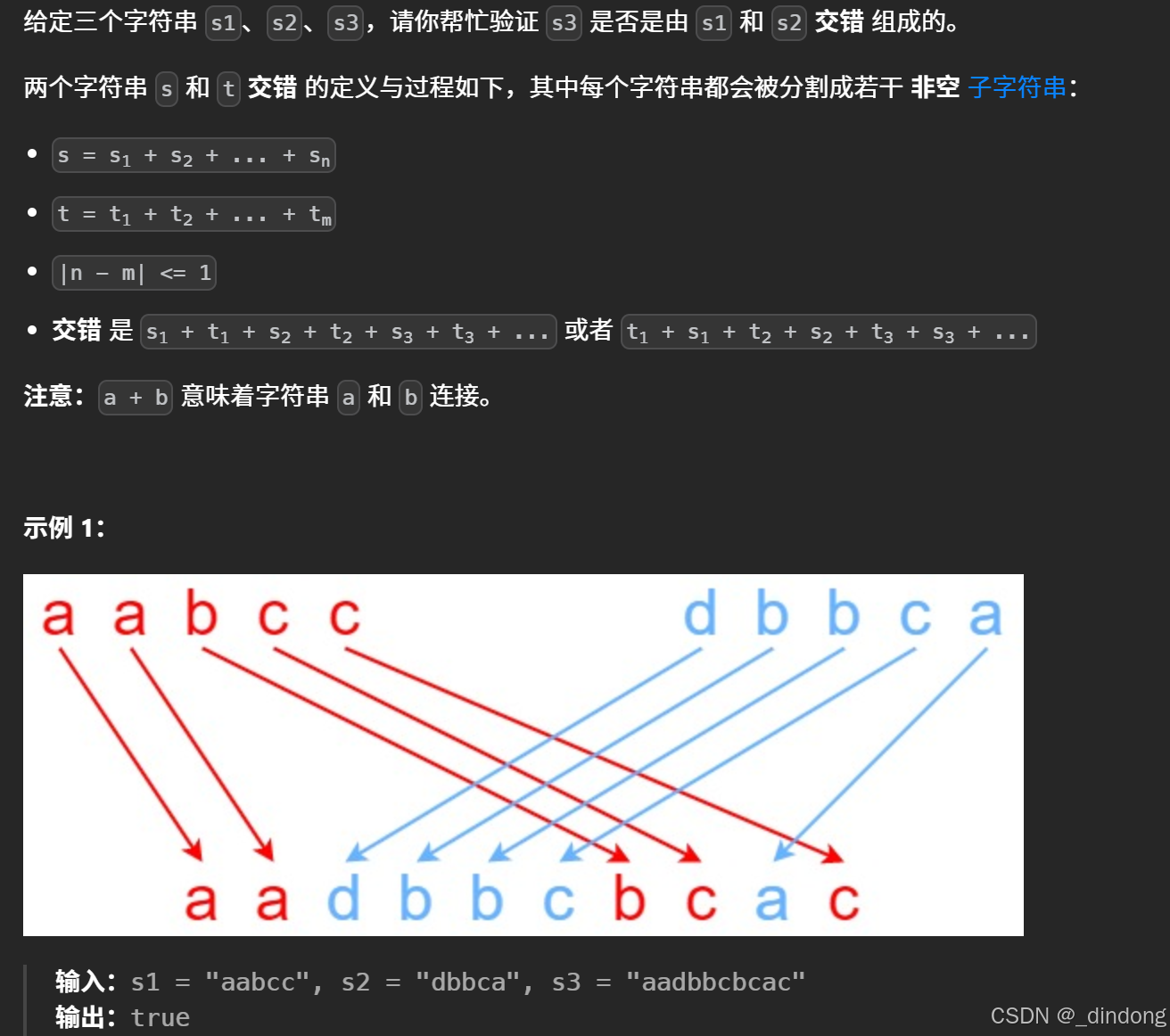

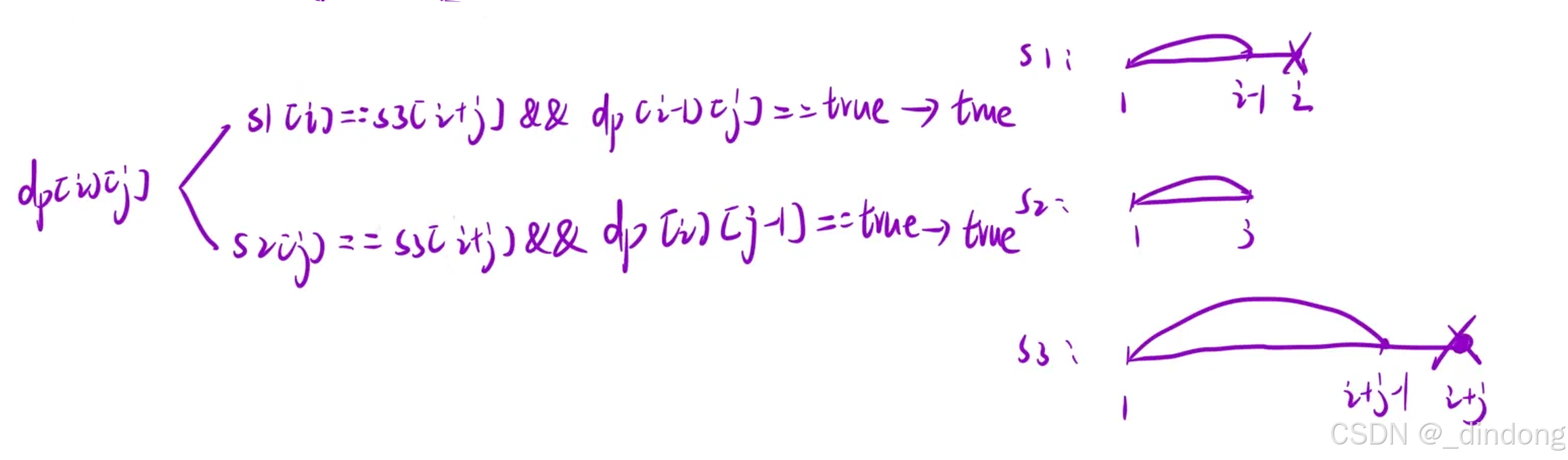
初始化:
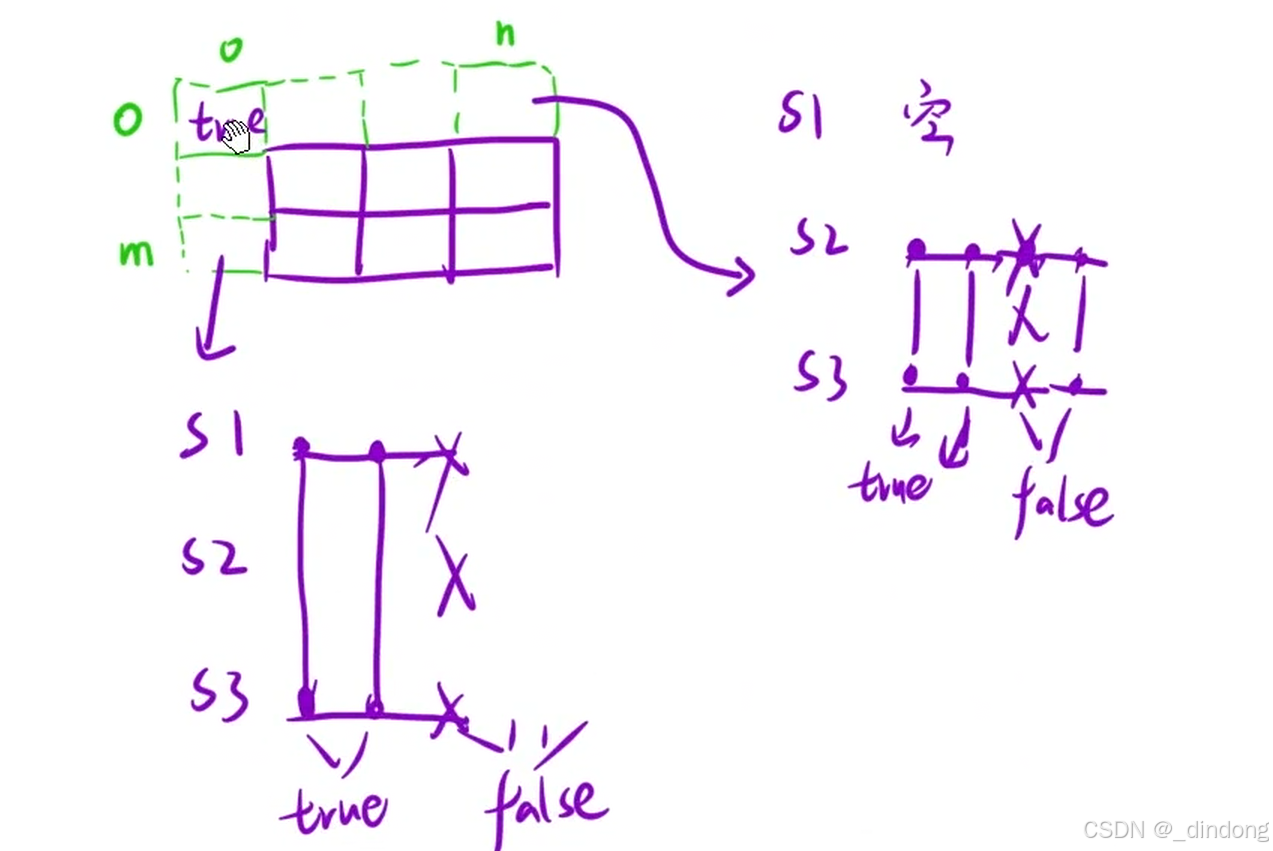
class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int m=s1.size(),n=s2.size();//特判一下if(m+n!=s3.size())return false;vector<vector<bool>> dp(m+1,vector<bool>(n+1));dp[0][0]=true;s1=" "+s1,s2=" "+s2,s3=" "+s3;//初始化for(int j=1;j<=n;++j){if(s2[j]==s3[j])dp[0][j]=true;else break;}for(int i=1;i<=m;++i){if(s1[i]==s3[i])dp[i][0]=true;else break;}//填表for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){dp[i][j]=(s1[i]==s3[i+j]&&dp[i-1][j])||(s2[j]==s3[i+j]&&dp[i][j-1]);}}return dp[m][n];}
};No.7 两个字符串的最小ASCII删除和
712. 两个字符串的最小ASCII删除和 - 力扣(LeetCode)

其实就是求最长公共子序列,求出子序列的ascii码值后用总的减去即可。


class Solution {
public:int minimumDeleteSum(string s1, string s2) {int m=s1.size(),n=s2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(s1[i-1]==s2[j-1])dp[i][j]=dp[i-1][j-1]+s1[i-1];else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}int sum=0;for(auto x:s1)sum+=x;for(auto x:s2)sum+=x;return sum-dp[m][n]*2;}
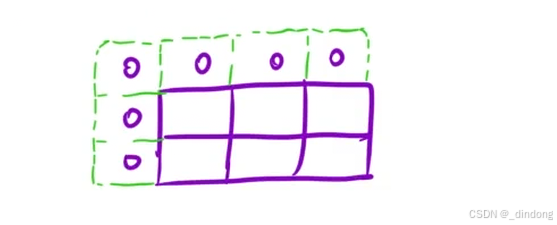
};No.8 最长重复子数组
718. 最长重复子数组 - 力扣(LeetCode)
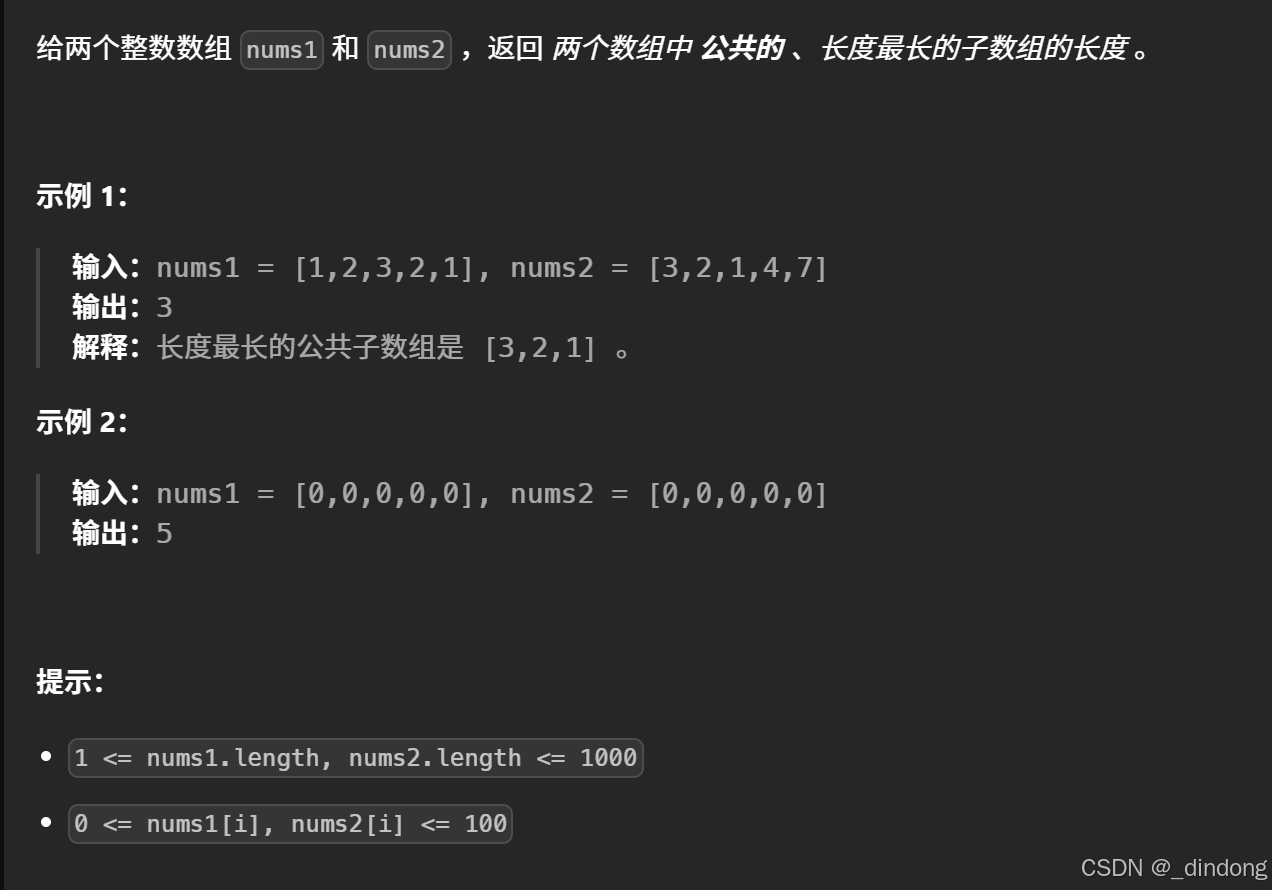

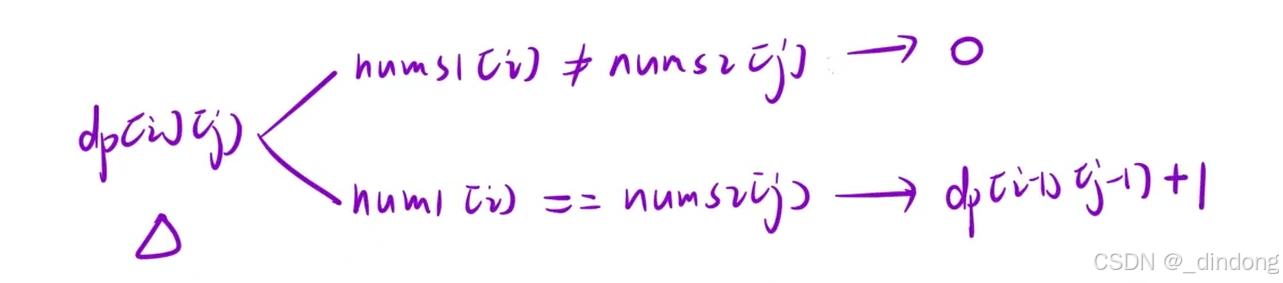
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size(), n = nums2.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));int ret = 0;for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {//符合条件才更新dp值以及ret,提高效率if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;ret = max(ret, dp[i][j]);}}}return ret;}
};此篇完。。。
