当前位置：首页 > news >正文

【洛谷】6 道题吃透堆的应用：模板堆、第 k 小、最小函数值等全攻略

news 2025/10/4 6:50:54

文章目录

模板堆
第k小
除2！
最小函数值
序列合并
舞蹈课

模板堆

题目描述

题目解析

模拟实现堆我们在数据结构初阶已经讲过了，这里小编不再过多赘述了，特别需要注意向下调整算法的逻辑，只要存在左孩子就要进循环，在循环中判断是否存在右孩子和比较左右孩子大小选其中小的为孩子结点，最后讲判断孩子结点是否比父节点小，把小的往上放。

代码

using namespace std;
#include <iostream>
#include <vector>const int N = 1e6 + 10;
int hpsize; //标记数组大小
int hp[N];void AdjustUp(int child)
{int parent = (child - 1) / 2;while (parent >= 0 && hp[child] < hp[parent]){//小的往上放swap(hp[child], hp[parent]);child = parent;parent = (child - 1) / 2;}
}void AdjustDown(int parent)
{int child = 2 * parent + 1;//小的往上放while (child < hpsize) //只要左孩子存在就继续检查{if (child + 1 < hpsize && hp[child + 1] < hp[child]){++child;}if (hp[child] >= hp[parent])return;swap(hp[child], hp[parent]);parent = child;child = 2 * parent + 1;}
}int main()
{int n = 0;cin >> n;while(n--){int op, x;cin >> op;if (op == 1){cin >> x;hp[hpsize] = x;AdjustUp(hpsize);++hpsize;}else if (op == 2){cout << hp[0] << endl;}else{if (hpsize >= 0){--hpsize;swap(hp[0], hp[hpsize]);AdjustDown(0);}}}return 0;
}

第k小

题目描述

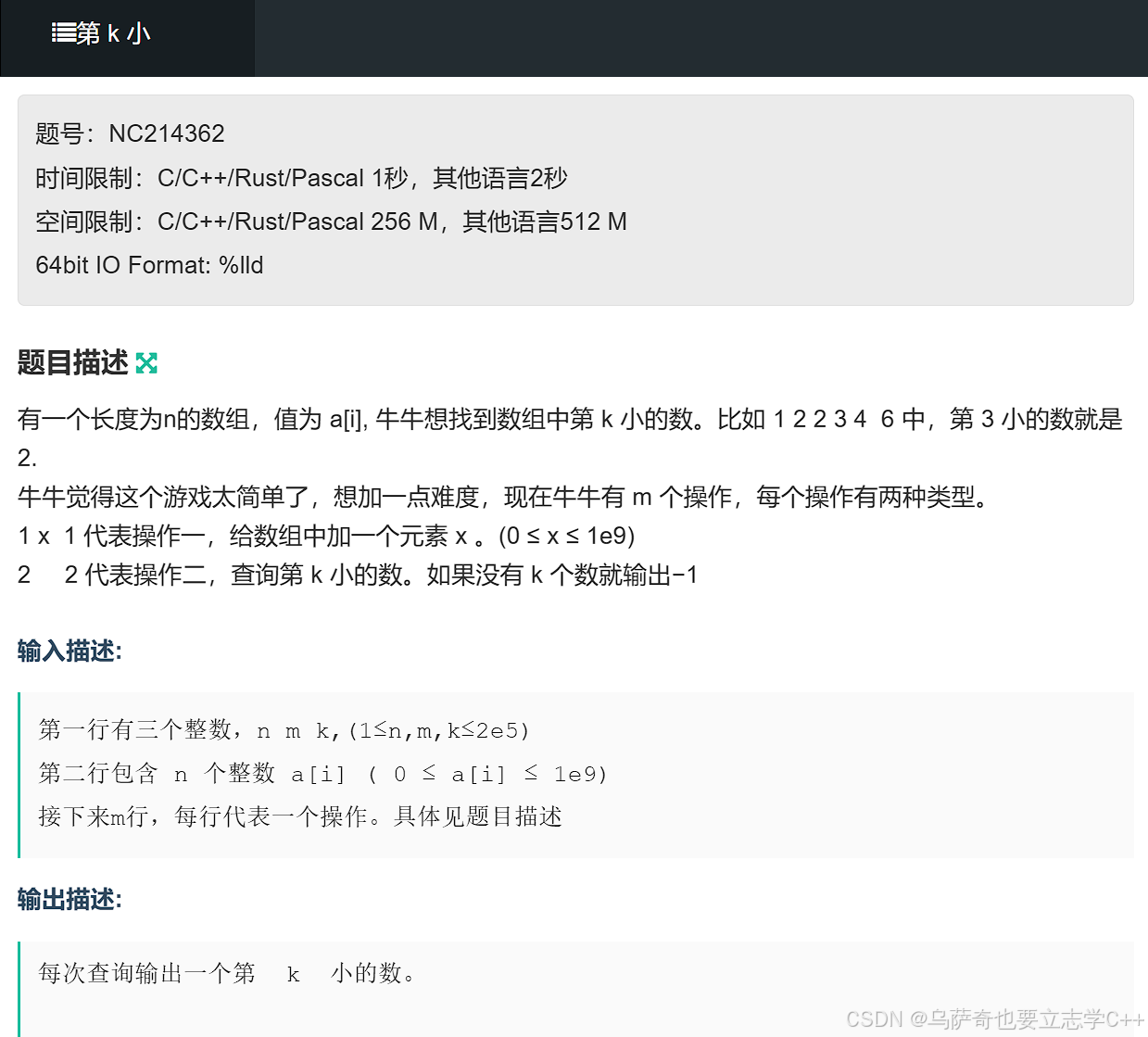
题目解析

本题是堆相关算法题的经典例题，本质就是topK问题，思路分两步走：
1、本题是求第K小，所以创建一个大根堆。
2、维护大根堆的大小为K即可，堆顶即为第K小。

代码

using namespace std;
#include <iostream>
#include <queue>int main()
{int n, m, k;cin >> n >> m >> k;priority_queue<int> hp;int tmp = 0;while(n--){cin >> tmp;hp.push(tmp);if(hp.size() > k){//当堆大小大于K时，堆顶即为多余数据//把堆顶数据pop掉hp.pop(); }}while(m--){int op, x = 0;cin >> op;if(op == 1){cin >> x;hp.push(x);if(hp.size() > k){hp.pop(); }}else{if(hp.size() == k){cout << hp.top() << endl;}else{int ret = -1;cout << ret << endl;}}}return 0;
}

除2！

题目描述

题目解析

本题乍一看没有思路，但是能想到利用堆来解决就简单了。题目要求选取数组中一个偶数除2后使数组中的数据和尽可能小，所以每次都要选数组中的最大偶数除2，那么如何选取数组中的最大偶数呢？当然是用堆啦，思路如下：
1、数据输入逻辑：
在读取输入数据时我们不把数据存入数组中，而是用一个变量num来记录输入数据的总和，当遇到偶数时把偶数数据入堆。
2、K次操作逻辑：
当K不为0且堆不为空才进入循环，先把堆中的最大数据除2并把结果写入变量t，然后把num减t，并判断t是否为偶数，若为偶数再把t入堆。
3、输出num。

还有本题需要注意数据大小，最后求和结果的最大情况是1e9*1e5 = 1e14，远大于int的存储范围1e9,所以最后的求和结果num要用 long long 类型来存。

代码

using namespace std;
#include <iostream>
#include <queue>typedef long long LL;int n, k, a;
LL num;
priority_queue<int> hp;int main()
{cin >> n >> k;for (int i = 0; i < n; i++){cin >> a;if (a % 2 == 0){//偶数才入堆hp.push(a);}num += a;}while (hp.size() && k--){//取堆中最大的偶数除2后写入变量tint t = hp.top() / 2;hp.pop();num -= t;if (t % 2 == 0){//若t还为偶数hp.push(t);}}cout << num;return 0;
}

最小函数值

题目描述

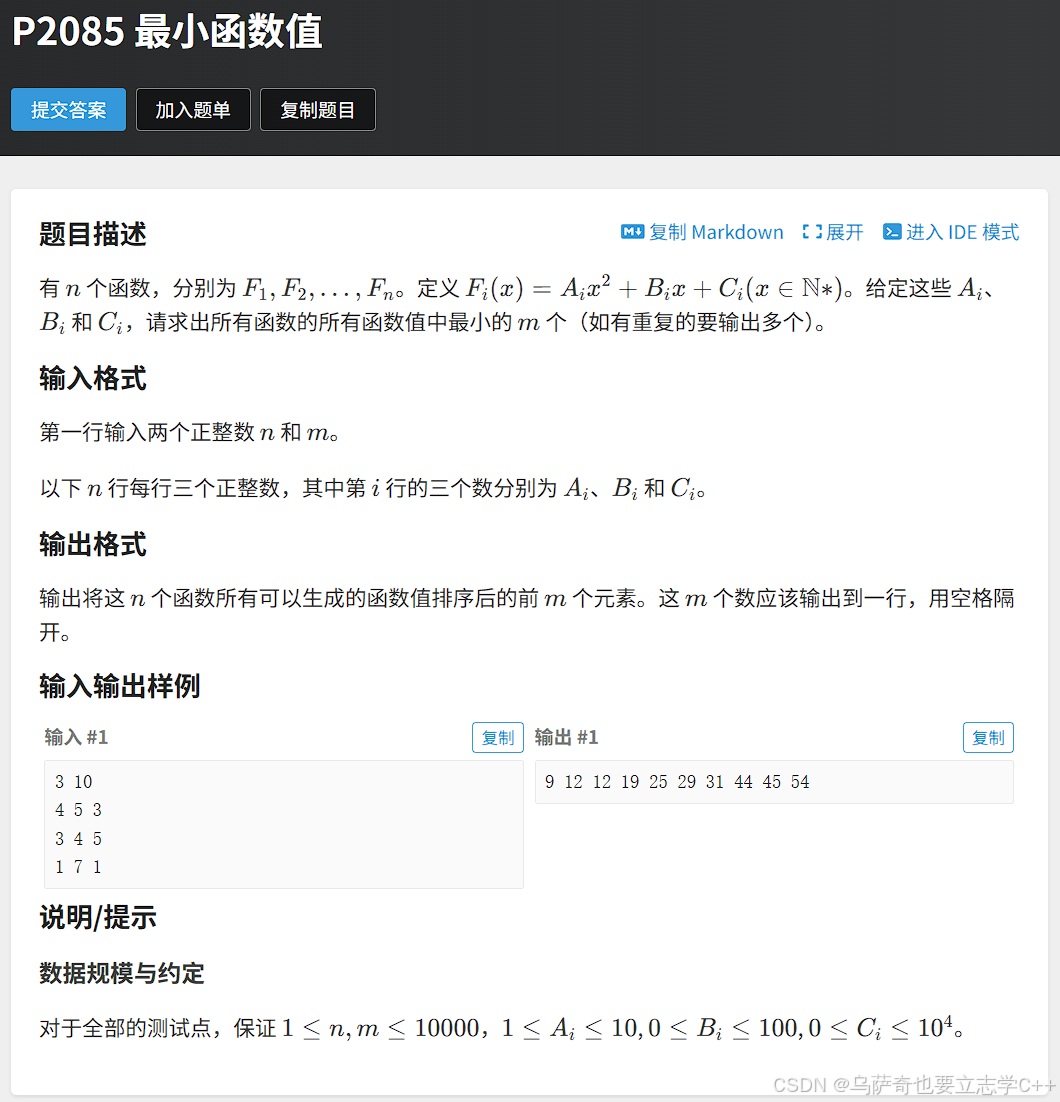
在这里插入图片描述
题目解析

对于本题来说审题很重要，一些信息都隐藏在题目中，比如x∈N∗，表示x是正整数，还有“以下 n 行每行三个正整数” 表示二次函数的系数都是整数，所以所有函数的对称轴都在x轴的左边。
有了上面的条件我们再结合二次函数的单调性可以得出一个结论，函数值随着x的增大是单调递增的，所以可以依据此结论来置定解决此题的思路：
1、先创建3个数组a[N], b[N], c[N]，用来存储每个函数的系数，函数Fi系数为a[i] b[i] c[i]。
2、因为函数值在x>0的范围是单调递增的，而题目规定x只能取正整数，所以每个函数的f(1)一定是该函数能取到的最小函数值，所以我们需要创建一个小根堆，并把所有函数的f(1)入堆。
3、m次操作，每次取堆顶元素并打印，然后把堆顶元素对应函数的下一个函数入堆，那么这里会出现一个问题，我们如何拿到下一个元素（x值）？而且如何知道该堆顶元素是由几号函数计算得来的？所以堆里的元素不能仅仅存函数值这一内置类型，而应该存一个结构体，把函数值、几号函数、函数x的取值打包放进结构体中，并在函数值入堆时把函数值所在的整个结构体入堆。
4、如果堆里存的时自定义类型就需要我们自己控制比较逻辑，这里的比较逻辑是只比较结构体里的函数值大小。控制比较逻辑有两种方法，一是仿函数，二是直接在结构体内部实现运算符重载operator<，本题实现仿函数比较麻烦，我们就采用方法二了，因为是小根堆，所以重载运算符内部应该是大于号。
5、写一个calc函数来计算函数值。

代码

using namespace std;
#include <iostream>
#include <queue>const int N = 1e4 + 10;
//存储函数系数A,B,C，函数Fi系数为a[i] b[i] c[i]
int a[N], b[N], c[N]; typedef struct node
{int result; //函数计算结果int fi;     //第几个函数int x;      //x取值//建小根堆传greaterbool operator<(const node& n) const{return result > n.result;}
}node;int calc(int fi, int x)
{//Ax^2 + Bx + Creturn a[fi] * x * x + b[fi] * x + c[fi];
}int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i] >> b[i] >> c[i];}priority_queue<node> hp;//把每个函数x取1的函数值入堆for (int i = 1; i <= n; i++){hp.push({ calc(i,1), i , 1});}// 1、输出堆顶最小值 // 2、把堆顶对应函数的下一个数据入堆while (m--){node top = hp.top();hp.pop();cout << top.result << " ";hp.push({ calc(top.fi, top.x + 1), top.fi , top.x + 1 });}return 0;
}

序列合并

题目描述
在这里插入图片描述
题目解析

法一：暴力求解
把所有相加结果都算出来再取最小的n个，这种方法我相信大家都能想到，但是本题数据范围还比较大，所以一定会超时的，我们需要想一个优化方案。
法二：优化解法
本题的优化解法和上一题思路很类似，本质思想就是利用局部单调递增或者单调不减的思想，局部数据中的最小值还在参与比较的时候其他数据我们可以先不看，当局部数据中的最小值输出后再把第二小的数据加入比较。
具体到本题的思路就是把输入的两个序列分别用两个数组存储，然后把第一行序列所有数据依次和第二行第一个数据相加并入堆，或者把第二行序列所有数据依次和第1行第一个数据相加并入堆，选取那行的第一个数据为基准都没有关系。然后打印堆中最小值，并把最小值所在列的下一个数据入堆。入堆时也和上一题类似，要把结构体整体入堆，结构体内存放了计算结果和两个相加数分别在各自数组的下标。

在这里插入图片描述

代码

using namespace std;
#include <iostream>
#include <queue>
#include <vector>const int N = 1e5 + 10;
int a[N], b[N]; //两个数组分别存储两个序列typedef struct node
{int result; //求和结果int i, j;   //i表示序列1编号，j表示序列2编号bool operator<(const node& node) const{//小根堆return result > node.result;}
}node;int main()
{int n;cin >> n;//用数组存储两个序列的值for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = 1; i <= n; i++){cin >> b[i];}//把第一行序列所有数据依次和第二行第一个数据相加并入堆priority_queue <node> hp;for (int i = 1; i <= n; i++){hp.push({ a[i] + b[1], i, 1});}//打印堆中最小值，并把最小值所在列的下一个数据入堆for (int i = 1; i <= n; i++){node top = hp.top();cout << top.result << " ";hp.pop();hp.push({ a[top.i] + b[top.j + 1], top.i, top.j + 1 });}return 0;
}

舞蹈课

题目描述
在这里插入图片描述
题目解析

这道题大体思路还是很好想的，把队列中的所有相邻异性组合拿出来，然后把每个组合的技术分差算出来存入堆中，然后依次取堆顶元素输出即可。
但是实际操作时还有许多细节需要注意：
1、相邻的一对异性出队后，他们的左右，有可能变成一对
既然要找到一对异性的左右两个人，就需要用到双向链表，所以需要用双向链表存队列。在提取结果时如果相邻异性组合的左右两边有人且为异性还需要把左右两边的人入堆。
2、堆中可能存在已经出队的人，比如下图：

在这里插入图片描述

我们会把（1，2）（2，3）（3，4）（4，5）（5，6）这五对异性全部入堆，若我们第一次取出（2，3）这对后，（1，2）（3，4）这两队都缺一个人，就没有意义了，应该让1和4重新组合成一对（就像父母离异后又重组家庭的哪种意思），呼应细节1。所以需要用数组st标记所有出队的人，便于后面输入结果时判断。
3、堆中存什么？
因为要拿到一对异性的左右两个人，所以堆里不能单单只存俩相邻异性的技术差，还需要要存两个异性的下标，所以也需要用一个结构体存储。

详细步骤分五步，详情看下面代码示例。

代码

补充：abs函数是用于计算数值绝对值的数学工具，能将负数转换为对应的正数，正数和 0 保持不变，需要包含math.h或者cmath头文件。（绝对值：absolute value）

using namespace std;
#include <iostream>
#include <queue>
#include <cmath>
#include <vector>const int N = 2e5 + 10;int s[N]; //数组s标记男1女0，默认全女，若为男则修改为1
int e[N], pre[N], ne[N]; //双向链表，e[i]用于存储每个人的技术值
bool st[N]; //用于标记st[i]这个人是否已经出队,1表示已出队//存储相邻异性之间的信息
struct node
{int d;    //两异性的分差int l, r; //两异性下标bool operator<(const node& n) const{//小根堆if (d != n.d){return d > n.d;}else if (l != n.l){return l > n.l;}else{return r > n.r;}}
};int main()
{int n;cin >> n;//1、初始化st数组for (int i = 1; i <= n; i++){char c;cin >> c;if (c == 'B'){s[i] = 1;}}//2、初始化双向链表for (int i = 1; i <= n; i++){int score;cin >> e[i];ne[i] = i + 1;pre[i] = i - 1;}//双向链表，头结点pre指向0，尾结点ne指向0ne[n] = pre[1] = 0;//3、将符合条件的一对异性入堆priority_queue<node> hp;for (int i = 2; i <= n; i++){if (s[i - 1] != s[i]){//符合异性条件hp.push({ abs(e[i - 1] - e[i]), i - 1, i });}}//4、提取结果并维护链表vector<node> ret;  //存储有多少对异性出列while (hp.size()){node top = hp.top();hp.pop();if (st[top.l] || st[top.r]){//两个人至少已经有一个人出队了，直接continuecontinue;}ret.push_back(top);int l = top.l, r = top.r, d = top.d;st[l] = st[r] = true;//还原链表ne[pre[l]] = ne[r];pre[ne[r]] = pre[l];//将还原链表后出现的新的异性组合入堆if (pre[l] != 0 && ne[r] != 0 && s[pre[l]] != s[ne[r]]){hp.push({ abs(e[pre[l]] - e[ne[r]]), pre[l], ne[r] });}}//5、输出结果cout << ret.size() << endl;for (auto e : ret){cout << e.l << " " << e.r << endl;}return 0;
}