基于物理信息神经网络（PINN）求解二维稳态对流-扩散方程的MATLAB实现

基于物理信息神经网络（PINN）求解二维稳态对流-扩散方程的MATLAB实现。以下是对代码的全面分析：

---

一、主要功能

1. 方程求解：求解二维稳态对流-扩散方程：U·∂C/∂x + V·∂C/∂y = D·(∂²C/∂x² + ∂²C/∂y²)
2. 多源数据融合：同时利用边界条件、测量数据和物理方程约束
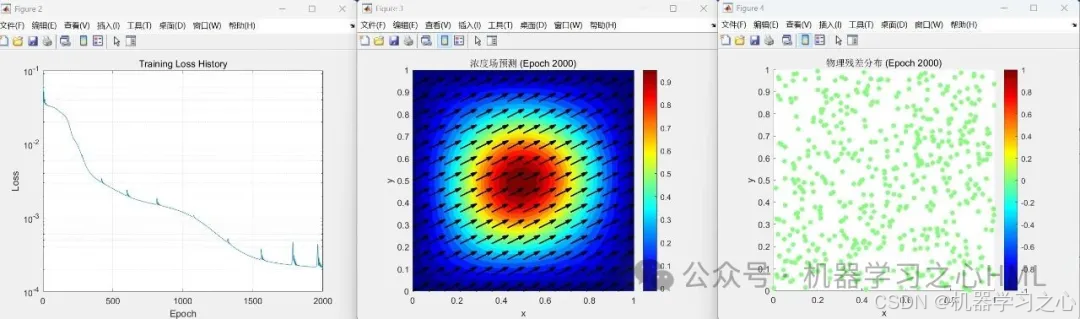
3. 浓度场预测：预测整个计算域内的浓度分布
4. 物理一致性验证：监控物理残差以确保解满足控制方程

---

二、逻辑关联

参数设置 → 数据生成 → 网络构建 → 训练循环 → 结果可视化↓           ↓           ↓         ↓          ↓物理参数   边界/测量/   神经网络   损失计算   浓度场+配置点生成   架构定义   梯度更新   残差图

数据流：

1. 边界数据：强制满足边界条件
2. 测量数据：提供真实观测值（含噪声）
3. 配置点：通过物理残差约束内部区域
4. 网络输出：预测整个区域的浓度场

---

三、算法步骤

阶段1：数据准备

1. 生成边界条件点（四边均匀分布）
2. 生成测量数据点（随机分布+高斯分布真实解+噪声）
3. 生成配置点（内部随机点，用于物理约束）

阶段2：网络构建

1. 创建4层全连接神经网络（每层32神经元）
2. 使用tanh激活函数
3. 单输出节点（浓度值）

阶段3：训练过程

1. 前向传播计算预测值
2. 自动微分计算浓度梯度（一阶和二阶）
3. 计算数据损失（边界+测量）和物理残差损失
4. Adam优化器更新网络参数
5. 定期可视化训练进度

阶段4：结果分析

1. 绘制预测浓度场
2. 可视化物理残差分布
3. 显示流场方向

---

四、技术路线

技术组件	实现方法
神经网络	多层感知机 + tanh激活
物理嵌入	自动微分计算PDE残差
优化算法	Adam优化器
自动微分	dlgradient高阶导数
数据加权	不同类型点赋予不同权重
可视化	实时训练监控

---

五、公式原理

控制方程（稳态对流-扩散）：

$$U\frac{\partial C}{\partial x}+V\frac{\partial C}{\partial y}=D\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}\right)$$

损失函数组成：

$$\mathcal{L}={\mathcal{L}}_{\text{data}}+{\mathcal{L}}_{\text{phys}}$$

数据损失：
$${\mathcal{L}}_{\text{data}}=\frac{1}{N}\sum _{i=1}^N{w}_i(C_{\text{pred}}^i-C_{\text{true}}^i{)}^2$$

物理残差损失：
$${\mathcal{L}}_{\text{phys}}=\frac{1}{M}\sum _{j=1}^M{w}_j{\left[U\frac{\partial C}{\partial x}+V\frac{\partial C}{\partial y}-D\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}\right)\right]}^2$$

---

六、参数设定

物理参数：

参数	值	含义
U	1.0	x方向对流速度
V	0.5	y方向对流速度
D	0.1	扩散系数

网络参数：

参数	值	含义
numLayers	4	隐藏层数量
numNeurons	32	每层神经元数
激活函数	tanh	非线性变换

训练参数：

参数	值	含义
numEpochs	2000	训练轮数
learningRate	0.001	学习率
physWeight	1.0	物理损失权重
dataWeight	1.0	数据损失权重

采样参数：

参数	值	含义
numBCPoints	100	边界条件点数
numDataPoints	50	测量数据点数
numCollPoints	1000	配置点数

---

七、运行环境

软件要求：

• MATLAB（推荐R2024b或更新版本）
• 必要工具箱：
  • Deep Learning Toolbox
  • 支持自动微分和dlnetwork的版本

计算特性：

• 自动微分：使用MATLAB的dlgradient计算高阶导数
• 批量训练：一次性处理所有训练点
• 实时可视化：训练过程中动态更新结果

---

八、应用场景

环境工程：

• 大气污染物扩散模拟
• 水体中污染物输运预测

工业应用：

• 化学反应器内物质分布
• 通风系统中空气污染物传播

科学研究：

• 多物理场耦合问题研究
• 逆向参数识别问题

---

总结

该代码实现了一个完整的PINN框架用于稳态对流-扩散问题，具有以下特点：

• 多源信息融合：巧妙结合边界条件、测量数据和物理方程
• 物理一致性：通过残差损失确保解满足控制方程
• 鲁棒性：能够处理带噪声的测量数据
• 可视化完善：提供训练过程监控和结果分析
• 模块化设计：清晰的函数分离便于修改和扩展

这种方法特别适合数据稀缺但物理规律明确的工程问题，为传统数值方法提供了有力的补充。

完整代码私信回复基于物理信息神经网络（PINN）求解二维稳态对流-扩散方程的MATLAB实现