当前位置： 首页 > news >正文

Python 中四种高级特征缩放技术详解：超越标准化的数据预处理

news 2025/9/29 8:32:28

引言

特征缩放是数据预处理中的关键步骤，广泛应用于统计建模、机器学习、数据可视化和数据分析等领域。虽然标准化（Standardization）和归一化（Min-Max Scaling）是最常用的方法，但在面对偏斜数据、异常值、非高斯分布等复杂情况时，这些基础方法往往力不从心。

本文将深入探讨四种高级特征缩放技术，帮助你应对这些挑战场景。

为什么需要高级特征缩放？

标准方法的局限性

  • 标准化（Z-score）：对异常值敏感，依赖均值标准差

  • 归一化（Min-Max）：受极端值影响大，破坏数据分布特性

高级技术的适用场景

  • 数据存在严重偏斜（Skewness）

  • 包含大量异常值（Outliers）

  • 需要强制转换为特定分布

  • 样本级别的标准化需求

1. 分位数变换（Quantile Transformer）

核心概念

分位数变换将输入数据的经验分位数映射到目标分布的分位数上，通常选择均匀分布或正态分布。这种方法不对数据分布做任何假设，具有极强的异常值鲁棒性。

数学原理

对于每个特征：

  1. 计算原始数据的经验累积分布函数

  2. 映射到目标分布的对应分位数

  3. 实现分布形态的转换

from sklearn.preprocessing import QuantileTransformer
import numpy as np
import matplotlib.pyplot as plt# 示例数据（包含异常值）
X = np.array([[10], [200], [30], [40], [5000]])# 应用到正态分布
qt_normal = QuantileTransformer(output_distribution='normal', random_state=0)
X_trans_normal = qt_normal.fit_transform(X)# 应用到均匀分布
qt_uniform = QuantileTransformer(output_distribution='uniform', random_state=0)
X_trans_uniform = qt_uniform.fit_transform(X)print("原始数据:", X.ravel())
print("分位数变换(正态):", X_trans_normal.ravel())
print("分位数变换(均匀):", X_trans_uniform.ravel())# 可视化对比
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
plt.hist(X, bins=5, alpha=0.7, color='blue')
plt.title('原始数据分布')plt.subplot(1, 3, 2)
plt.hist(X_trans_normal, bins=5, alpha=0.7, color='green')
plt.title('分位数变换(正态)')plt.subplot(1, 3, 3)
plt.hist(X_trans_uniform, bins=5, alpha=0.7, color='red')
plt.title('分位数变换(均匀)')plt.tight_layout()
plt.show()

原始数据: [  10  200   30   40 5000]
分位数变换(正态): [-5.19933758  0.67448975 -0.67448975  0.          5.19933758]
分位数变换(均匀): [0.01 0.8  0.4  0.6  0.99]

应用场景

  • 异常值处理：压缩极端值，增强模型稳定性

  • 分布转换：将任意分布转换为目标分布

  • 非参数统计：不依赖分布假设的分析方法

2. 幂变换（Power Transformer）

核心概念

幂变换通过寻找最优的λ参数，使数据更接近正态分布。主要包括两种方法：

  • Box-Cox变换：仅适用于正值数据

  • Yeo-Johnson变换：适用于正负值和零值

数学原理

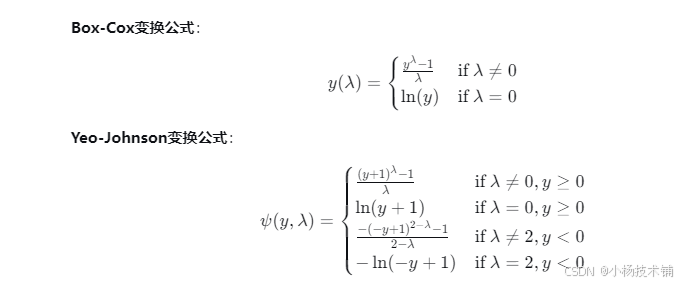
Python实现

from sklearn.preprocessing import PowerTransformer
import numpy as np
import matplotlib.pyplot as plt# 正值数据示例
X_positive = np.array([[1.0], [2.0], [3.0], [4.0], [5.0]])# Box-Cox变换
pt_boxcox = PowerTransformer(method='box-cox', standardize=True)
X_boxcox = pt_boxcox.fit_transform(X_positive)print("原始数据(正值):", X_positive.ravel())
print("Box-Cox变换:", X_boxcox.ravel())# 混合数据示例（包含负值）
X_mixed = np.array([[-2.0], [-1.0], [0.0], [1.0], [2.0]])# Yeo-Johnson变换
pt_yeojohnson = PowerTransformer(method='yeo-johnson', standardize=True)
X_yeojohnson = pt_yeojohnson.fit_transform(X_mixed)print("\n原始数据(混合):", X_mixed.ravel())
print("Yeo-Johnson变换:", X_yeojohnson.ravel())# 可视化对比
fig, axes = plt.subplots(2, 2, figsize=(12, 8))# 正值数据分布
axes[0, 0].hist(X_positive, bins=5, alpha=0.7, color='blue')
axes[0, 0].set_title('原始正值数据')axes[0, 1].hist(X_boxcox, bins=5, alpha=0.7, color='green')
axes[0, 1].set_title('Box-Cox变换后')# 混合数据分布
axes[1, 0].hist(X_mixed, bins=5, alpha=0.7, color='red')
axes[1, 0].set_title('原始混合数据')axes[1, 1].hist(X_yeojohnson, bins=5, alpha=0.7, color='orange')
axes[1, 1].set_title('Yeo-Johnson变换后')plt.tight_layout()
plt.show()

输出结果

原始数据(正值): [1. 2. 3. 4. 5.]
Box-Cox变换: [-1.50121999 -0.64662521  0.07922595  0.73236192  1.33625733]

原始数据(混合): [-2. -1.  0.  1.  2.]
Yeo-Johnson变换: [-1.41421356 -0.70710678  0.          0.70710678  1.41421356]

应用场景

  • 正态性转换：满足线性模型的正态分布假设

  • 方差稳定：处理方差异质性（Heteroscedasticity）

  • 偏斜校正：纠正右偏或左偏分布

3. 鲁棒缩放（Robust Scaling）

核心概念

鲁棒缩放使用对异常值不敏感的中位数和四分位距（IQR）进行缩放，相比基于均值标准差的标准化方法更具鲁棒性。

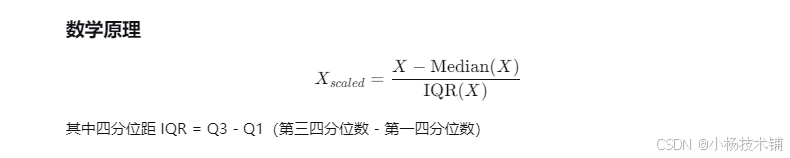
Python实现

from sklearn.preprocessing import RobustScaler
import numpy as np
import matplotlib.pyplot as plt# 包含异常值的数据
X = np.array([[10], [20], [30], [40], [1000]])scaler = RobustScaler()
X_trans = scaler.fit_transform(X)print("原始数据:", X.ravel())
print("鲁棒缩放:", X_trans.ravel())# 与标准化的对比
from sklearn.preprocessing import StandardScalerstandard_scaler = StandardScaler()
X_standard = standard_scaler.fit_transform(X)print("标准化结果:", X_standard.ravel())# 可视化对比
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
plt.bar(range(len(X)), X.ravel(), color='blue', alpha=0.7)
plt.title('原始数据')plt.subplot(1, 3, 2)
plt.bar(range(len(X_trans)), X_trans.ravel(), color='green', alpha=0.7)
plt.title('鲁棒缩放')plt.subplot(1, 3, 3)
plt.bar(range(len(X_standard)), X_standard.ravel(), color='red', alpha=0.7)
plt.title('标准化')plt.tight_layout()
plt.show()

输出结果

原始数据: [  10   20   30   40 1000]
鲁棒缩放: [-1.  -0.5  0.   0.5 48.5]
标准化结果: [-0.47401349 -0.46065649 -0.44729949 -0.43394249  1.81591196]

应用场景

  • 异常值处理：金融数据、传感器数据等包含极端值的情况

  • 稳健建模：增强模型对异常值的抵抗能力

  • 数据探索：获得更真实的数据分布视图

4. 单位向量缩放（Unit Vector Scaling）

核心概念

单位向量缩放将每个样本缩放为单位范数，重点关注样本间的相对大小而非绝对数值。常用的范数包括：

  • L1范数：绝对值之和，关注稀疏性

  • L2范数：欧几里得距离，保持几何关系

Python实现

from sklearn.preprocessing import Normalizer
import numpy as np# 示例数据
X = np.array([[1, 2, 3], [4, 5, 6]])# L2范数归一化
normalizer_l2 = Normalizer(norm='l2')
X_l2 = normalizer_l2.transform(X)# L1范数归一化
normalizer_l1 = Normalizer(norm='l1')
X_l1 = normalizer_l1.transform(X)print("原始数据:")
print(X)
print("\nL2归一化:")
print(X_l2)
print("\nL1归一化:")
print(X_l1)# 验证范数计算
print("\n验证L2范数:")
for i in range(X_l2.shape[0]):norm = np.linalg.norm(X_l2[i], 2)print(f"样本{i}的L2范数: {norm:.6f}")print("\n验证L1范数:")
for i in range(X_l1.shape[0]):norm = np.linalg.norm(X_l1[i], 1)print(f"样本{i}的L1范数: {norm:.6f}")

输出结果

原始数据:
[[1 2 3]
[4 5 6]]

L2归一化:
[[0.26726124 0.53452248 0.80178373]
[0.45584231 0.56980288 0.68376346]]

L1归一化:
[[0.16666667 0.33333333 0.5       ]
[0.26666667 0.33333333 0.4       ]]

验证L2范数:
样本0的L2范数: 1.000000
样本1的L2范数: 1.000000

验证L1范数:
样本0的L1范数: 1.000000
样本1的L1范数: 1.000000

应用场景

  • 文本挖掘：TF-IDF向量、词袋模型

  • 推荐系统：用户行为向量标准化

  • 相似度计算：余弦相似度、距离度量

  • 图像处理：像素向量归一化

技术选型指南

技术适用场景优点缺点
分位数变换异常值处理、分布转换异常值鲁棒性强、可指定目标分布计算成本较高、可能过拟合
幂变换正态性转换、偏斜校正改善分布特性、参数自动优化对零和负值有限制（Box-Cox）
鲁棒缩放包含异常值的数据异常值免疫、计算效率高不改变数据分布形状
单位向量缩放样本级标准化、相似度计算保持相对关系、适用于稀疏数据丢失绝对大小信息

实践建议

  1. 数据探索先行：在应用任何缩放技术前，先通过直方图、Q-Q图等了解数据分布

  2. 交叉验证：在机器学习流程中，使用交叉验证评估不同缩放技术的影响

  3. 管道集成：将特征缩放集成到scikit-learn管道中，确保数据泄露防护

  4. 领域知识：结合业务背景选择最合适的缩放方法

完整示例：综合比较

from sklearn.datasets import load_iris
from sklearn.preprocessing import (QuantileTransformer, PowerTransformer, RobustScaler, Normalizer, StandardScaler)
import pandas as pd
import matplotlib.pyplot as plt# 加载数据
iris = load_iris()
X = iris.data
feature_names = iris.feature_names# 应用不同缩放技术
scalers = {'Original': None,'Standard': StandardScaler(),'Quantile(Normal)': QuantileTransformer(output_distribution='normal'),'Power(Yeo-Johnson)': PowerTransformer(method='yeo-johnson'),'Robust': RobustScaler(),'UnitVector(L2)': Normalizer(norm='l2')
}# 可视化比较
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.ravel()for idx, (name, scaler) in enumerate(scalers.items()):if scaler is None:X_scaled = Xelse:X_scaled = scaler.fit_transform(X)# 显示第一个特征的分布axes[idx].hist(X_scaled[:, 0], bins=20, alpha=0.7)axes[idx].set_title(f'{name}\n(Feature: {feature_names[0]})')axes[idx].set_xlabel('Value')axes[idx].set_ylabel('Frequency')plt.tight_layout()
plt.show()

总结

高级特征缩放技术为解决复杂数据预处理问题提供了有力工具。选择合适的技术需要综合考虑数据特性、业务需求和模型假设。通过本文的介绍和代码示例，希望你能在实际项目中灵活运用这些技术，提升数据质量和模型性能。

记住：没有最好的特征缩放方法，只有最适合当前问题的方法。

http://www.dtcms.com/a/419200.html

相关文章：

  • TypeScript语法（类型注解:、类型断言as、联合类型|、类型守卫typeof、交叉类型、类型别名type、类型保护is）
  • 做网站时版权怎么写新型网络营销推广方式
  • 机器学习——朴素贝叶斯详解
  • 2025汽车芯片有哪些看点，将会带来哪些黑科技？
  • 管道机器人（in-pipe / in-line）避障
  • 建设监理有限责任公司网站怎么做微信点击网站打赏看片
  • LeetCode:79.跳跃游戏Ⅱ
  • 【FPGA 开发分享】如何在 Vivado 中使用 PLL IP 核生成多路时钟
  • Jupyter Notebook 两种模式：编辑模式 命令模式
  • 网站首页结构国际新闻最新消息今天 新闻
  • 网站建设投标文档阿里云市场网站建设
  • 前端用什么开发工具？常用前端开发工具推荐与不同阶段的选择指南
  • web核心—Tomcat的下载/配置/mavenweb项目创建/通过mavenweb插件运行web项目
  • 强化学习 持续任务
  • 数据集制作--easy-dataset
  • 学校网站管理方案做网站需要哪些手续
  • 大连建设工程网站惠州建设集团公司网站
  • 中国城市市政公用设施水平数据（1990-2022年）
  • 【算法笔记】二叉树递归解题套路及其应用
  • 洋气的传媒公司名字永州seo快速排名
  • 充电桩智能升级方案之微波雷达模块WT4101A-C04
  • 1、Lombok入门与环境配置：理解Lombok作用、配置IDE与构建工具
  • 【PostgreSQL内核学习：哈希聚合（HashAgg）执行流程与函数调用关系分析】
  • 选择邯郸网站建设电商网站如何备案
  • 易旅游网站建设东莞有哪些做推广的网站
  • [算法练习]第三天：定长滑动窗口
  • 山海织锦·时序成画——连云港城市旅游宣传片的策划、拍摄与制作全流程解构
  • Mariadb服务器
  • 现代Web存储技术（三）：配额监控与自动化清理机制
  • 高并发系统的海量数据处理架构