机器学习——朴素贝叶斯详解

一、概率论知识

1. 概念：朴素贝叶斯是概率值进行分类的一种机器学习算法
2. 条件概率：表示事件A在另外一个事件B已经发生的条件下的发生概率，$P(A|B)$
3. 联合概率：表示多个条件同时成立的概率，$P(AB)=P(A)P(B|A)=P(B)P(A|B)$
4. 贝叶斯公式：$$P(C|W)=\frac{P(W|C)P(C)}{P(W)}$$
5. 朴素贝叶斯：为了简化联合概率的计算，朴素贝叶斯在贝叶斯基础上增加了特征条件独立假设，即：特征之间是互为独立的
6. 拉普拉斯平滑系数：为了避免概率值为0，我们分别在分子和分母上加一个系数：
   $$P(F_1|C)=\frac{N_i+\alpha }{N+\alpha m}$$
   • 其中$\alpha$是拉普拉斯平滑系数，一般指定为1
   • $N_i$是$F_1$中符合条件C的样本数量
   • N是在条件C下所有样本的总数
   • m表示所有独立和样本的总数

二、特征降维

2.1 为什么需要特征降维

用于训练的数据集特征对模型的性能有着极其重要的作用。如果训练数据中包含一些不重要的特征，可能导致模型的泛化性能不佳。例如：

1. 某些特征的取值较为接近，其包含的信息较少
2. 我们希望特征独立存在，对预测产生影响，具有相关性的特征可能并不会给模型带来更多的信息，但是并不是说相关性完全无用。

2.2 低方差过滤法

我们知道:

1. 特征方差小：某个特征大多样本的值比较相近
2. 特征方差大：某个特征很多样本的值都有差别

from sklearn.feature_selection import VarianceThreshold
import pandas as pd# 1. 读取数据集
data = pd.read_csv('data/垃圾邮件分类数据.csv')
print(data.shape) # (971, 25734)# 2. 使用方差过滤法
transformer = VarianceThreshold(threshold=0.1)
data = transformer.fit_transform(data)
print(data.shape) # (971, 1044)

2.3 主成分分析（PCA）

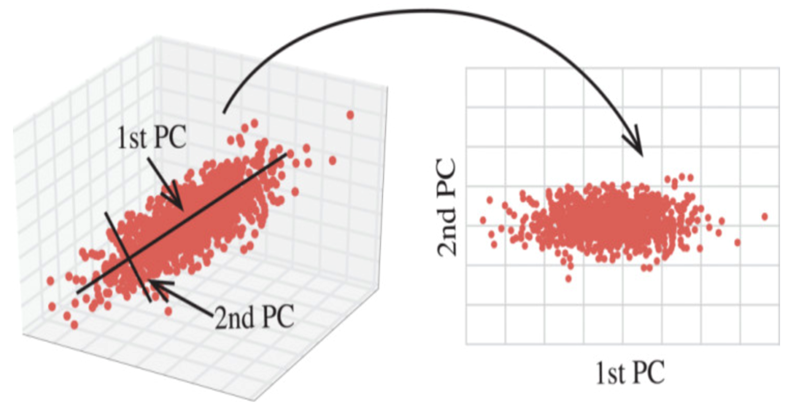
1. PCA通过对数据维数进行压缩，尽可能降低元数据的维数（复杂度），损失少量信息，在此过程中可能会舍弃原有数据、创造新变量

from sklearn.decomposition import PCA
from sklearn.datasets import load_iris# 1. 加载数据集
x, y = load_iris(return_X_y=True)
print(x[:5])
# [[5.1 3.5 1.4 0.2]
#  [4.9 3.  1.4 0.2]
#  [4.7 3.2 1.3 0.2]
#  [4.6 3.1 1.5 0.2]
#  [5.  3.6 1.4 0.2]]# 2. 保留指定比例的信息
transformer = PCA(n_components=0.95)
x_pca = transformer.fit_transform(x)
print(x_pca[:5])
# [[-2.68412563  0.31939725]
#  [-2.71414169 -0.17700123]
#  [-2.88899057 -0.14494943]
#  [-2.74534286 -0.31829898]
#  [-2.72871654  0.32675451]]# 3. 保留指定数量特征
transformer = PCA(n_components=2)
x_pca = transformer.fit_transform(x)
print(x_pca[:5])
# [[-2.68412563  0.31939725]
# [-2.71414169 -0.17700123]
# [-2.88899057 -0.14494943]
# [-2.74534286 -0.31829898]
# [-2.72871654  0.32675451]]

2.4 相关系数法

1. 相关系数：反应特征列之间（变量之间）密切相关程度

• 相关系数的值介于-1与+1之间，即$-1<=r<=1$
  • 当 r>0 时，表示两个变量正相关；当 r<0 时，表示两个变量负相关
  • 当 |r|=1 时，表示两变量为完全相关；当 |r|=0 时，表示两变量间无相关关系
  • 当 0<|r|<1 时。表示两变量存在一定程度的关系，且 |r| 越接近1，线性相关越密切；|r| 越接近0，线性相关越弱
• |r|<0.4 为低度相关；0.4<=|r|<0.7 为显著相关；0.7 <= |r|<1为高度线性相关

2. 皮尔逊相关系数：
   $$r=\frac{n\sum xy-\sum x\sum y}{\sqrt{n\sum x^2-(\sum x{)}^2}\sqrt{n\sum y^2-(\sum y{)}^2}}$$

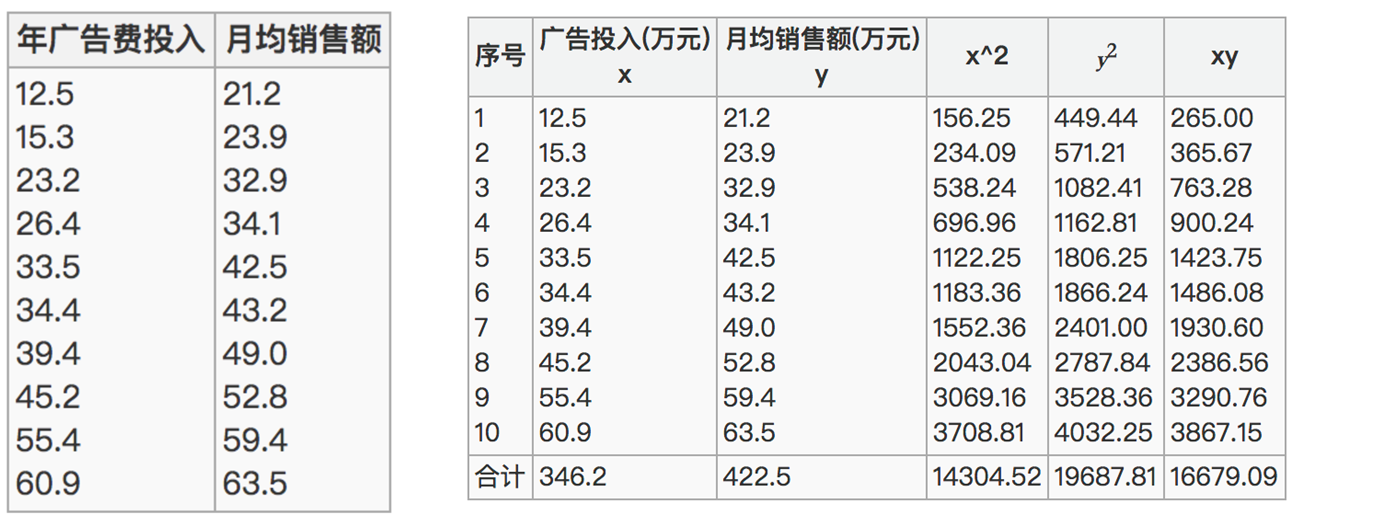
已知广告投入x特征与月均销售额y之间的关系，经过皮尔逊相关系数的计算，呈现高度相关

$$\frac{10\times 1667\dot{9}.09-346.2\times 422.5}{\sqrt{10\times 14304.52-346.2^2}\sqrt{10\times 19687.81-422.5^2}}=0.9942$$

3. 斯皮尔曼相关系数：$$RankIC=1-\frac{6\sum d_i^2}{n(n^2-1)}，\{\begin{array}{l}其中n为等级个数\\ d为成对变量的等级差数\end{array}$$

import pandas as pd
from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
from scipy.stats import spearmanr
from sklearn.datasets import load_iris# 1. 读取数据集(鸢尾花数据集)
data = load_iris()
data = pd.DataFrame(data.data, columns=data.feature_names)# 2. 皮尔逊相关系数
corr = pearsonr(data['sepal length (cm)'], data['sepal width (cm)'])
print(corr, '皮尔逊相关系数:', corr[0], '不相关性概率:', corr[1])
# (-0.11756978413300204, 0.15189826071144918) 
# 皮尔逊相关系数: -0.11756978413300204 不相关性概率: 0.15189826071144918# 3. 斯皮尔曼相关系数
corr = spearmanr(data['sepal length (cm)'], data['sepal width (cm)'])
print(corr, '斯皮尔曼相关系数:', corr[0], '不相关性概率:', corr[1])
# SpearmanrResult(correlation=-0.166777658283235, pvalue=0.04136799424884587) 
# 斯皮尔曼相关系数: -0.166777658283235 不相关性概率: 0.04136799424884587