强化学习 持续任务
阿尔伯塔大学【中英⚡强化学习|Reinforcement Learning Specialization】-misuseds-稍后再看-哔哩哔哩视频

solidworks环境就是持续任务?


A
这张图展示了强化学习中回报(Returns)的递归性质,这是理解价值函数和动态规划的基础。我们来逐步解析这个公式:
📌 标题:Recursive nature of returns
(回报的递归性质)
🔹 公式推导:
原始定义:
Gt≐Rt+1+γRt+2+γ2Rt+3+γ3Rt+4+⋯Gt≐Rt+1+γRt+2+γ2Rt+3+γ3Rt+4+⋯
其中:
- GtGt:从时间步 tt 开始的总折扣回报(discounted return)
- Rt+1,Rt+2,…Rt+1,Rt+2,…:未来各时刻的即时奖励(rewards)
- γ∈[0,1]γ∈[0,1]:折扣因子,表示对未来奖励的重视程度(越接近1,越看重长远)
🔁 递归分解:
我们将右边的表达式进行分组:
Gt=Rt+1+γ(Rt+2+γRt+3+γ2Rt+4+⋯ )Gt=Rt+1+γ(Rt+2+γRt+3+γ2Rt+4+⋯)
注意到括号中的部分其实就是 从 t+1t+1 开始的回报 Gt+1Gt+1!
所以可以写成:
Gt=Rt+1+γGt+1Gt=Rt+1+γGt+1
✅ 关键结论:
回报具有递归结构:当前时刻的回报等于:
- 当前下一步的即时奖励 Rt+1Rt+1
- 加上未来回报 Gt+1Gt+1 的折扣值 γGt+1γGt+1
这就是著名的贝尔曼方程(Bellman Equation) 的基础形式。
🎯 图中注释解释:
- 中间蓝色框标出的部分是 Gt+1Gt+1,即从 t+1t+1 开始的回报。
- 箭头指向说明:“This is just Gt+1Gt+1”
- 中文翻译:“现在,我们得到了一个递归方程,左边是 GtGt,右边是 Gt+1Gt+1。”
💡 应用意义:
这个递归关系使得我们可以:
- 用动态规划方法求解最优策略;
- 在时序差分(TD)学习中更新价值函数;
- 构建基于价值迭代或策略迭代的算法。
✅ 总结一句话:
“未来的回报可以被拆解为‘立即奖励’加上‘未来回报的折现’。”
这正是强化学习中价值函数递归定义的核心思想。
B
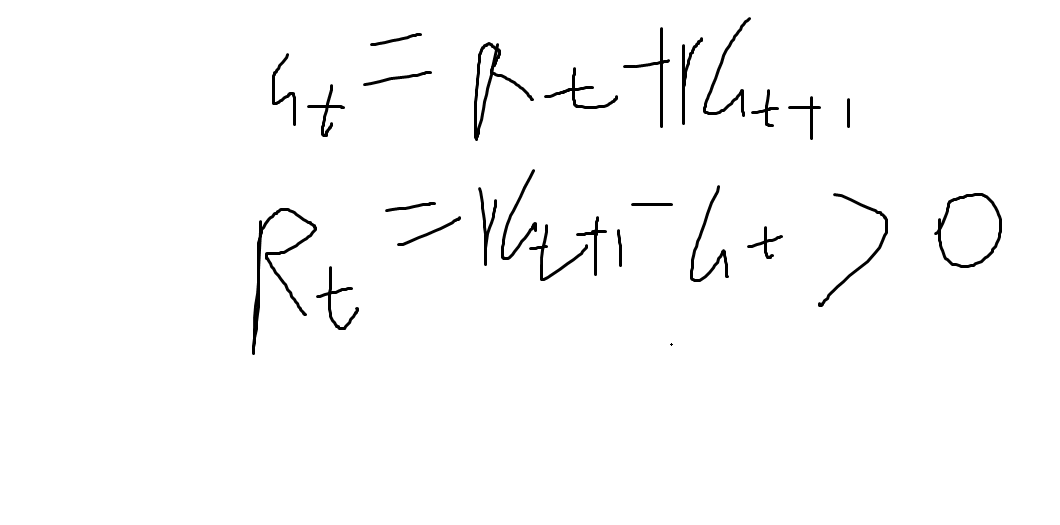
你写的这两个公式是强化学习中**时序差分学习(Temporal Difference Learning)**的核心公式,特别常见于 TD(0) 算法。我们来逐个分析:
公式 1:
Gt=Rt+1+γGt+1Gt=Rt+1+γGt+1
这是回报(Return)的递归定义。
- GtGt:从时间步 tt 开始的累积回报(discounted return)。
- Rt+1Rt+1:在时间步 t+1t+1 获得的即时奖励。
- γγ:折扣因子,0≤γ≤10≤γ≤1,用于权衡未来奖励的重要性。
- Gt+1Gt+1:从时间步 t+1t+1 开始的累积回报。
这个公式表示:当前时刻的回报等于立即奖励加上未来回报的折现值。
✅ 这是马尔可夫决策过程(MDP)中回报的标准定义。
公式 2:
Rt=γGt+1−GtRt=γGt+1−Gt
这个公式看起来有点问题,让我们仔细看看。
它写的是:
Rt=γGt+1−GtRt=γGt+1−Gt
但根据第一个公式:
Gt=Rt+1+γGt+1⇒Rt+1=Gt−γGt+1Gt=Rt+1+γGt+1⇒Rt+1=Gt−γGt+1
所以正确的形式应该是:
Rt+1=Gt−γGt+1或等价地Rt+1=Gt−γGt+1Rt+1=Gt−γGt+1或等价地Rt+1=Gt−γGt+1
但你写的公式是:
Rt=γGt+1−Gt=−(Gt−γGt+1)=−Rt+1Rt=γGt+1−Gt=−(Gt−γGt+1)=−Rt+1
这说明你可能是把下标搞混了。
正确的 TD 错误(TD Error)表达式:
在 TD 学习中,我们使用 TD 错误 来更新价值函数:
δt=Rt+1+γV(St+1)−V(St)δt=Rt+1+γV(St+1)−V(St)
其中:
- V(St)V(St) 是状态 StSt 的估计价值。
- Rt+1Rt+1 是下一时刻的奖励。
- γV(St+1)γV(St+1) 是下一状态的折现价值。
这个 δtδt 就是 TD 错误,用来更新价值函数。
可能你想表达的是什么?
如果你是在写 TD(0) 更新规则,那么你应该看到:
V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]
其中括号里的就是 TD 错误。
总结:
你写的两个公式中:
- Gt=Rt+1+γGt+1Gt=Rt+1+γGt+1 ✅ 正确(回报的递归定义)
- Rt=γGt+1−GtRt=γGt+1−Gt ❌ 错误(符号和下标不对)
正确的关系是:
Rt+1=Gt−γGt+1Rt+1=Gt−γGt+1
或者更常见的是用 TD 错误的形式:
δt=Rt+1+γV(St+1)−V(St)δt=Rt+1+γV(St+1)−V(St)
如果你是在做价值迭代、策略评估,或者想实现 TD 学习,可以继续问我!我可以帮你推导完整的算法流程 😊
