灵犀互娱笔试

选择题

建立堆的算法？

建立堆（Heapify）是构建一个满足堆性质的数据结构的过程。堆通常是一个完全二叉树，分为最大堆（父节点 >= 子节点）和最小堆（父节点 <= 子节点）。最常用的建立堆的算法是 自底向上的“下沉”（Sift-Down）法。

算法：自底向上构建堆（Sift-Down Method）

核心思想
将给定的数组视为一个完全二叉树。
从最后一个非叶子节点开始，向前遍历到根节点。
对每个节点执行 “下沉”（Sift-Down） 操作，使其满足堆的性质。
为什么从最后一个非叶子节点开始？

叶子节点没有子节点，天然满足堆的性质，无需处理。
最后一个非叶子节点的索引是 n/2 - 1（n 为数组长度，索引从0开始）。

另一种方法：自顶向下（Insertion Method）

思路：逐个将元素插入堆中，每次插入后执行“上浮”（Sift-Up）操作。
时间复杂度：(O(n \log n))，比自底向上的方法慢。
适用场景：数据是动态流入的，需要边插入边建堆。

什么是LSD基数排序？

核心思想
LSD 基数排序是一种非比较型的整数排序算法。它不通过直接比较元素的大小来排序，而是：

按位处理 ：将每个待排序的数字看作是由多个“位”（digit）组成的序列。
从低位到高位：从最不重要的一位（个位）开始，依次向最重要的位（如百位、千位等）进行处理。
稳定排序： 在每一位上，使用一个稳定的排序算法（通常是计数排序）对该位上的数字进行排序。
关键点： 由于每一轮排序都是稳定的（即相等元素的相对位置在排序后不变），当处理到更高位时，之前低位的排序结果会被“保留”，从而最终得到一个完全有序的序列。

执行过程示例
对 [170, 45, 75, 90, 2, 802, 2, 66] 进行 LSD 基数排序：

按个位排序：
个位数字: [0, 5, 5, 0, 2, 2, 2, 6]
排序后: [170, 90, 45, 75, 2, 802, 2, 66]
按十位排序：
十位数字: [7, 9, 4, 7, 0, 0, 0, 6]
排序后: [2, 802, 2, 45, 66, 170, 75, 90]
按百位排序：
百位数字: [0, 8, 0, 0, 0, 1, 0, 0]
排序后: [2, 2, 45, 66, 75, 90, 170, 802]
注意：在十位和百位排序中，个位相同的数字（如 2, 802, 2）的相对顺序在稳定排序下得以保持。

稳定排序算法和非稳定排序算法

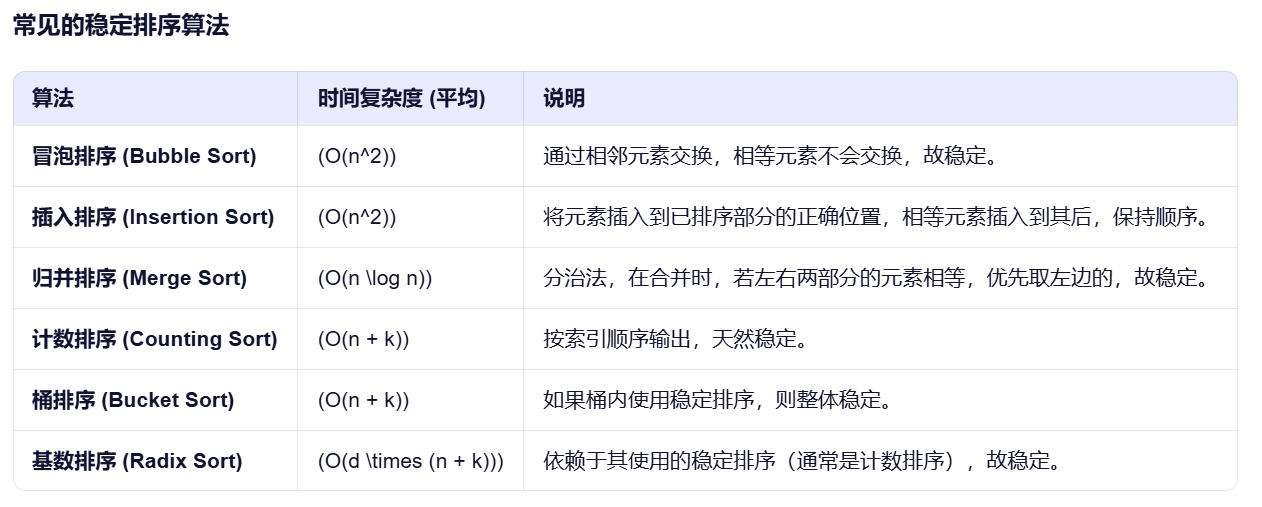
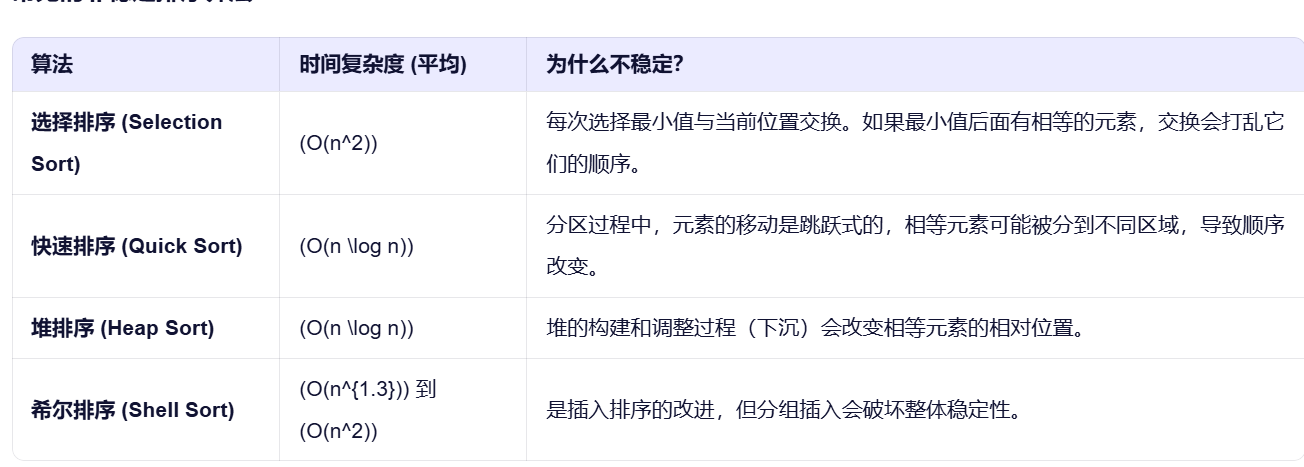
数据库的四大范式

数据库的“范式”（Normal Form）是关系数据库设计中的一系列规范，旨在减少数据冗余、提高数据一致性、避免数据更新异常。虽然常被提及的是前几范式，但严格来说，有五个主要范式（1NF 到 5NF），其中前四个（1NF, 2NF, 3NF, BCNF）最为常用和重要。

第一范式

原子性 (Atomicity)：表中的每个字段（列）都必须是不可再分的最小数据单元。

第二范式

消除部分函数依赖 (Partial Dependency)。
表中的所有非主属性（非主键字段）都必须完全函数依赖于整个主键，而不是只依赖于主键的一部分。

第三范式

消除传递函数依赖 (Transitive Dependency)。
表中的所有非主属性都必须直接函数依赖于主键，而不能通过其他非主属性间接依赖。

第四范式

更严格的函数依赖控制。
对于表中的每一个非平凡的函数依赖 X → Y，X 必须是超键 (Superkey)。
简单说：决定因素（X）必须是候选键。

常用的对称加密和非对称加密算法有哪些？

算法题

给定一个整数a,求最小的因式排列，使得其组成的数字最小，且各个位数的数字乘积为a

要找到一个整数 (a) 的最小因式排列（即组成的数字最小，且各个位数的数字乘积为 (a)），我们需要遵循以下步骤：

分解因子： 首先需要找出所有可能的单个数字（从2到9）作为 (a) 的因子。这是因为任何大于9的数字不能作为一个单独的位出现在最终结果中。
贪心算法： 从最大的可能因子开始（即9），尽可能多地使用这个因子去除 (a)。如果当前因子无法整除 (a)，则尝试下一个较小的因子，直到2为止。
检查余数： 如果在上述过程中，(a) 能够被完全分解为这些因子的乘积而没有余数，则收集这些因子作为结果的一部分。如果有余数且该余数大于1，则说明 (a) 无法仅通过2到9的数字相乘得到，因此在这种情况下问题无解。
排序与组合： 最后将收集到的因子按从小到大的顺序排列，并将它们组合成一个数字，这样就能保证组成的数字是最小的。

给定一个数组，问该数组是否严格递增，或者删除一个数之后能够严格递增？

这是一个经典的算法问题，可以在线性时间 (O(n)) 内解决。
关键因素：针对坏点，不能贪心的只删除前面的元素，否则针对示例 1 3 5 2 6 则不适用

解题思路
我们需要判断一个数组是否满足以下两个条件之一：

数组本身就是严格递增的。
数组中恰好存在一个元素，删除它之后，剩余的数组是严格递增的。
核心观察
如果数组不是严格递增的，那么必然存在至少一个位置 i，使得 nums[i] <= nums[i-1]。我们称这样的位置为“坏点”。
我们的目标是检查是否可以通过最多删除一个元素来消除所有的“坏点”。
关键策略
当发现一个“坏点”（即 nums[i] <= nums[i-1]）时，我们有两种选择来尝试修复：

删除 nums[i-1]：前提是 nums[i-2] < nums[i] （如果 i-2 >= 0），这样 nums[i] 才能接在 nums[i-2] 后面。
删除 nums[i]：前提是 nums[i-1] < nums[i+1] （如果 i+1 < n），这样 nums[i+1] 才能接在 nums[i-1] 后面。
算法步骤
遍历数组，寻找第一个“坏点” i（即 nums[i] <= nums[i-1]）。
如果没有找到“坏点”，说明数组已经是严格递增的，返回 True。
如果找到了“坏点” i，我们尝试两种删除方案：
方案一：删除 nums[i-1]。检查删除后是否能满足 nums[i-2] < nums[i]。
方案二：删除 nums[i]。检查删除后是否能满足 nums[i-1] < nums[i+1]。
只要其中一种方案可行，就继续检查剩余部分是否严格递增。如果都不可行，则返回 False。

使用栈实现

是的，可以使用栈来实现这个问题。虽然这个问题有更直接的双指针或一次遍历的解法，但使用栈是一个非常直观且可行的思路。

使用栈的思路
核心思想是：

模拟删除过程：我们尝试遍历数组，将元素尽可能地压入栈中，同时维护栈内元素的严格递增性质。
处理“坏点”：当遇到一个新元素 nums[i] 小于或等于栈顶元素时，说明出现了“坏点”。
决策删除哪个：此时，我们需要决定是删除栈顶元素（旧元素） 还是删除当前元素（新元素）。
最多删除一次：我们只允许进行一次删除操作。如果删除一次后仍然无法维持递增，或者需要第二次删除，则返回 False。

算法步骤

初始化一个空栈 stack 和一个计数器 deletions = 0 来记录已删除的元素个数。
遍历数组中的每个元素 num：
如果栈为空，或者 num > stack[-1]（栈顶），则直接将 num 压入栈。
否则（num <= stack[-1]），说明出现了“坏点”，需要删除一个元素：
检查是否已经删除过：如果 deletions >= 1，说明已经删过一次了，不能再删，直接返回 False。
决策删除哪个：
方案一： 删除栈顶元素。检查删除后，num 是否能接在新的栈顶之后。即，如果栈中只有一个元素（len(stack) == 1）或者 num > stack[-2]（倒数第二个元素），那么可以删除栈顶，然后将 num 压入。
方案二： 删除当前元素 num。如果方案一不可行，我们可以选择不压入 num（相当于删除它），并增加 deletions 计数。
如果两种方案都不可行，则返回 False。
遍历结束后，如果 deletions <= 1，返回 True。

java如何构建字典树？

在 Java 中构建字典树（Trie，又称前缀树）是一个常见的数据结构应用，常用于字符串的快速查找、前缀匹配、自动补全等场景。

public class Trie {// Trie 的内部节点类private static class TrieNode {// 存储子节点，假设只处理小写字母 a-zprivate TrieNode[] children;// 标记从根到当前节点的路径是否构成一个完整的单词private boolean isEndOfWord;public TrieNode() {children = new TrieNode[26]; // 26 个小写字母isEndOfWord = false;}}// Trie 的根节点private final TrieNode root;/*** 初始化 Trie 对象*/public Trie() {root = new TrieNode();}/*** 向 Trie 中插入一个单词* @param word 要插入的单词*/public void insert(String word) {TrieNode current = root;for (char ch : word.toCharArray()) {int index = ch - 'a'; // 将字符映射到 0-25if (current.children[index] == null) {current.children[index] = new TrieNode();}current = current.children[index];}// 标记单词结束current.isEndOfWord = true;}/*** 搜索 Trie 中是否存在完整的单词* @param word 要搜索的单词* @return 如果存在返回 true，否则返回 false*/public boolean search(String word) {TrieNode node = searchPrefix(word);return node != null && node.isEndOfWord;}/*** 判断 Trie 中是否有以给定前缀开头的单词* @param prefix 给定的前缀* @return 如果存在返回 true，否则返回 false*/public boolean startsWith(String prefix) {return searchPrefix(prefix) != null;}/*** 辅助方法：搜索前缀，返回最后一个节点* @param prefix 前缀* @return 最后一个节点，如果不存在则返回 null*/private TrieNode searchPrefix(String prefix) {TrieNode current = root;for (char ch : prefix.toCharArray()) {int index = ch - 'a';if (current.children[index] == null) {return null;}current = current.children[index];}return current;}// ==================== 额外功能：可选 ====================/*** 删除一个单词（递归实现）* @param word 要删除的单词* @return 如果删除成功返回 true*/public boolean delete(String word) {return delete(root, word, 0);}private boolean delete(TrieNode current, String word, int index) {if (index == word.length()) {// 到达单词末尾if (!current.isEndOfWord) {return false; // 单词不存在}current.isEndOfWord = false;// 如果该节点没有子节点，可以删除（向上回溯时处理）return current.children == null || noChildren(current);}char ch = word.charAt(index);int charIndex = ch - 'a';TrieNode childNode = current.children[charIndex];if (childNode == null) {return false; // 单词不存在}boolean shouldDeleteChild = delete(childNode, word, index + 1);if (shouldDeleteChild) {current.children[charIndex] = null; // 删除子节点// 返回当前节点是否也应该被删除return !current.isEndOfWord && noChildren(current);}return false;}/*** 检查节点是否有任何子节点*/private boolean noChildren(TrieNode node) {for (TrieNode child : node.children) {if (child != null) {return false;}}return true;}// ==================== 测试方法 ====================public static void main(String[] args) {Trie trie = new Trie();// 插入单词trie.insert("apple");trie.insert("app");trie.insert("application");trie.insert("apply");// 搜索完整单词System.out.println(trie.search("app"));        // trueSystem.out.println(trie.search("apple"));      // trueSystem.out.println(trie.search("appl"));       // false// 前缀查询System.out.println(trie.startsWith("app"));    // trueSystem.out.println(trie.startsWith("ban"));    // false// 删除单词trie.delete("app");System.out.println(trie.search("app"));        // falseSystem.out.println(trie.startsWith("app"));    // true (因为 apple 还在)trie.delete("apple");System.out.println(trie.startsWith("app"));    // true (application, apply 还在)}
}