【R语言验证统计量的渐进分布】

一、模拟常见分布（一个连续型随机变量和一个离散型随机变量）：

1. 产生随机数；

2. 绘制该分布的直方图、理论概率密度函数p.d.f、实际密度函数CDF和核估计；

3. 绘制经验分布函数ECDF(阶梯型曲线);

R语言代码如下：

# 连续型随机变量模拟（均匀分布）

set.seed(123)  # 设置随机种子

n <- 100 # 样本量

a <- 2 # 均匀分布下界

b <- 8 # 均匀分布上界

# 1. 生成均匀分布随机数

uniform_data <- runif(n, min = a, max = b)

uniform_data

# 2. 绘制直方图、理论密度函数、实际密度函数和核密度估计

dev.new()  # 新建绘图窗口

# 绘制密度直方图

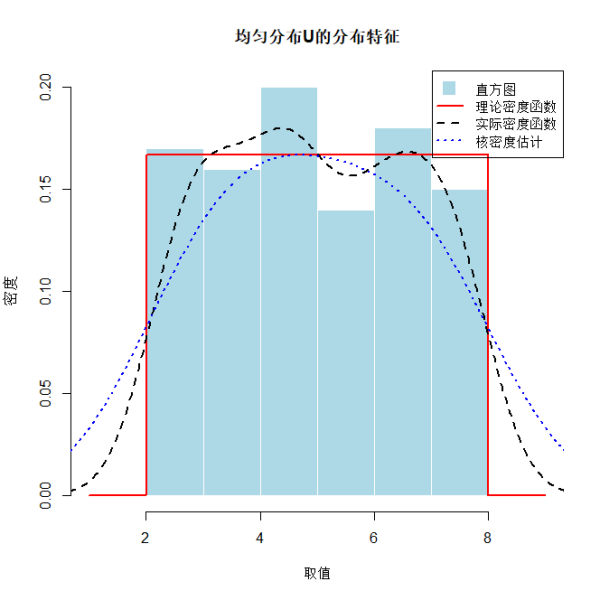
hist(uniform_data, freq = FALSE,

     main = paste0("均匀分布U的分布特征"),

     xlab = "取值", ylab = "密度", col = "lightblue", border = "white",

     xlim = c(a-1, b+1))  # 扩展x轴范围便于观察

# 添加理论概率密度函数

x <- seq(a-1, b+1, length.out = 1000)

# 构造均匀分布理论密度：区间外为0，区间内为1/(b-a)

theo_density <- ifelse(x >= a & x <= b, 1/(b - a), 0)

lines(x, theo_density, col = "red", lwd = 2, lty = 1)

# 添加实际密度函数（基于样本的密度估计）

lines(density(uniform_data, adjust = 1), col = "black", lwd = 2, lty = 2)

# 添加核密度估计（平滑后的密度估计）

lines(density(uniform_data, adjust = 2), col = "blue", lwd = 2, lty = 3)

# 添加图例

legend("topright",

       legend = c("直方图", "理论密度函数", "实际密度函数", "核密度估计"),

       col = c("lightblue", "red", "black", "blue"),

       lwd = c(NA, 2, 2, 2),

       lty = c(NA, 1, 2, 3),

       pch = c(15, NA, NA, NA),

       pt.cex = 2)

# 3. 绘制经验分布函数(阶梯型曲线)

dev.new()  # 新建绘图窗口

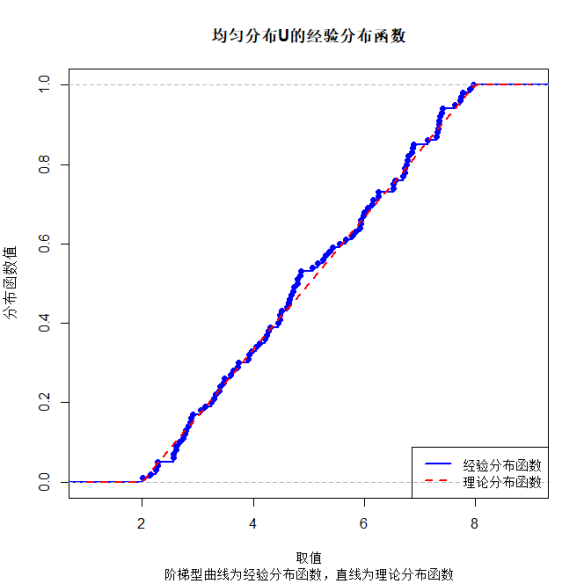
plot(ecdf(uniform_data), main = paste0("均匀分布U的经验分布函数"),

     xlab = "取值", ylab = "分布函数值", col = "blue", lwd = 2,

     xlim = c(a-1, b+1))  # 扩展x轴范围

# 添加理论分布函数（均匀分布的CDF为分段函数）

theo_ecdf <- function(x) {

  ifelse(x < a, 0,

         ifelse(x > b, 1, (x - a)/(b - a))

  )

}

curve(theo_ecdf(x), add = TRUE, col = "red", lwd = 2, lty = 2)

legend("bottomright", legend = c("经验分布函数", "理论分布函数"),

       col = c("blue", "red"), lwd = 2, lty = c(1, 2))

title(sub = "阶梯型曲线为经验分布函数，直线为理论分布函数")

# 离散型随机变量模拟（二项分布）

set.seed(123)

n <- 100  # 样本量

# 1. 生成随机数（二项分布，n=10，p=0.5）

discrete_data <- rbinom(n, size = 10, prob = 0.5)

# 2. 绘制直方图、理论概率、实际概率和核密度估计

dev.new()  # 新建绘图窗口

# 计算频率分布

counts <- table(discrete_data)

bar_heights <- counts / sum(counts)  # 转换为概率

# 绘制直方图

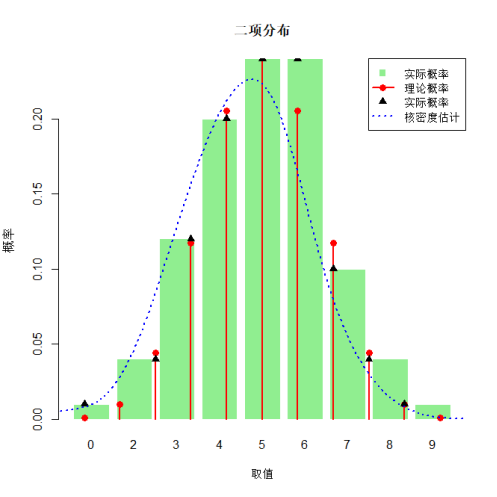
barplot(bar_heights, main = "二项分布",

        xlab = "取值", ylab = "概率", col = "lightgreen", border = "white",

        names.arg = names(counts))

# 添加理论概率函数

x <- 0:10

理论概率 <- dbinom(x, size = 10, prob = 0.5)

points(x + 0.5, 理论概率, col = "red", pch = 16, cex = 1.2)  # 调整位置使点与柱对齐

lines(x + 0.5, 理论概率, col = "red", lwd = 2, lty = 1, type = "h")

# 添加实际概率（用点表示）

points(as.numeric(names(counts)) + 0.5, bar_heights, col = "black", pch = 17, cex = 1.2)

# 添加核密度估计（离散数据的平滑估计）

lines(density(discrete_data, adjust = 1.5), col = "blue", lwd = 2, lty = 3)

# 添加图例

legend("topright",

       legend = c("实际概率", "理论概率", "实际概率", "核密度估计"),

       col = c("lightgreen", "red", "black", "blue"),

       pch = c(15, 16, 17, NA),

       lty = c(NA, 1, NA, 3),

       lwd = c(NA, 2, NA, 2),

       pt.cex = 1.2)

# 3. 绘制经验分布函数及阶梯型曲线

dev.new()  # 新建绘图窗口

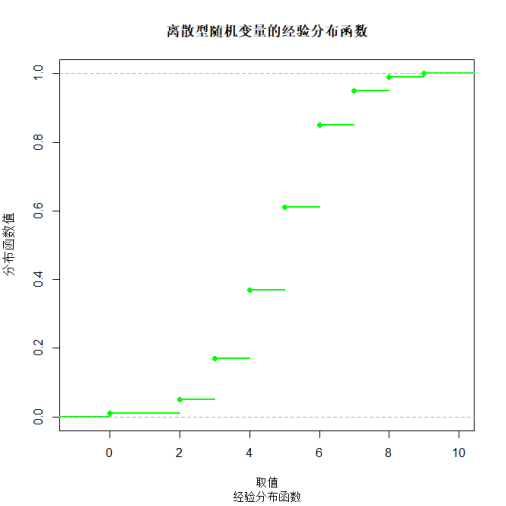
plot(ecdf(discrete_data), main = "离散型随机变量的经验分布函数",

     xlab = "取值", ylab = "分布函数值", col = "green", lwd = 2)

title(sub = "经验分布函数")

• 用R语言进行统计量的渐进分布验证：

1. 给定均匀分布，产生N维容量为n的随机数；

2. 计算样本均值、样本方差、样本标准差、t化统计量、中位数、Q1、Q3等统计量；

3. 检验上述统计量的分布是否为正态分布；

R语言代码如下：

# 设置随机数种子

set.seed(123)

# 参数设置

N <- 10000  # 重复试验次数

n <- 100  # 每个样本的容量

dist_params <- c(0, 1)  # 均匀分布参数：U(0,1)

# 1.生成N个容量为n的均匀分布随机样本

# 生成N×n的矩阵，每行是一个样本

samples <- matrix(runif(N * n, min = dist_params[1], max = dist_params[2]),

                  nrow = N, ncol = n)

# 2.计算各统计量（按行计算，每行对应一个样本的统计量）

# 样本均值

sample_mean <- rowMeans(samples)

# 样本方差（自由度为n-1）

sample_var <- apply(samples, 1, var)

# 样本标准差

sample_sd <- sqrt(sample_var)

# t化统计量=(均值 - 总体均值) / (标准差 / sqrt(n))

# 均匀分布U(0,1)的总体均值为0.5，总体方差为1/12

pop_mean <- mean(dist_params)  # U(a,b)均值为(a+b)/2

t_stat <- (sample_mean - pop_mean) / (sample_sd / sqrt(n))

# 中位数

sample_median <- apply(samples, 1, median)

# 第一四分位数(Q1)

sample_q1 <- apply(samples, 1, quantile, probs = 0.25)

# 第三四分位数(Q3)

sample_q3 <- apply(samples, 1, quantile, probs = 0.75)

# 3. 统计量正态性检验函数

test_normality <- function(stat, stat_name) {

  # K-S检验：p 值越大越支持正态分布假设

  ks_result <- ks.test(stat, "pnorm",

                       mean = mean(stat), # 使用样本均值作为正态分布均值

                       sd = sd(stat)) # 使用样本标准差作为正态分布标准差

  

  # QQ图：通过样本分位数与理论正态分位数的对比，若点近似落在直线上，说明越接近正态分布

  par(mfrow = c(1, 1))  # 单图模式

  qqnorm(stat, main = paste(stat_name, "的QQ图"))

  qqline(stat, col = "red", lwd = 2)

  

  # 输出K-S检验结果

  cat("\n---", stat_name, "的K-S检验结果---\n")

  print(ks_result)

  cat("--------------------------------------------------\n")

}

# 对各统计量进行正态性检验

test_normality(sample_mean, "样本均值")

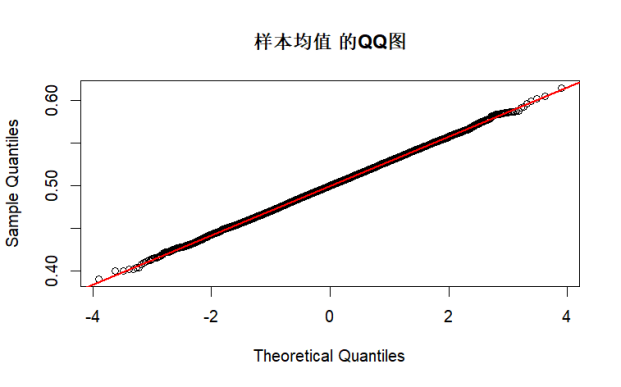
test_normality(sample_var, "样本方差")

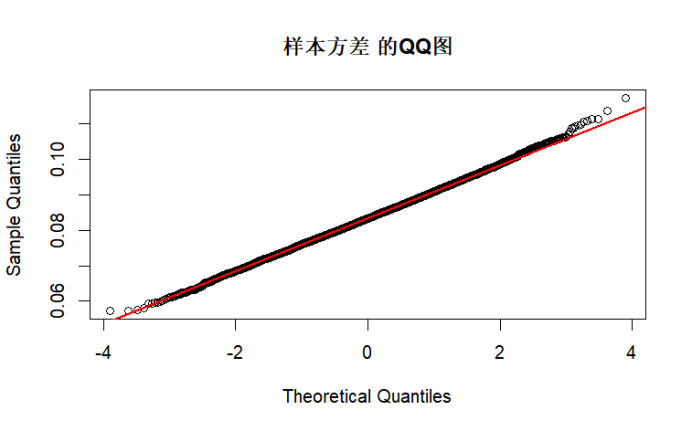
test_normality(sample_sd, "样本标准差")

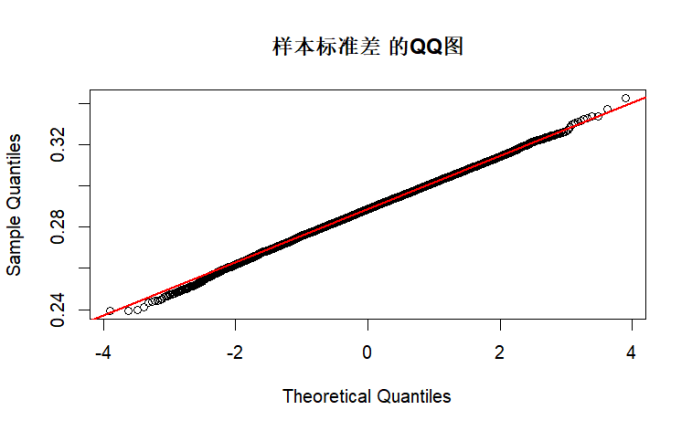
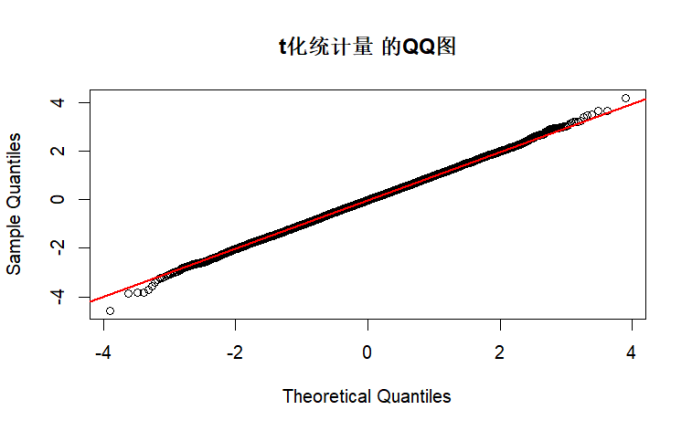
test_normality(t_stat, "t化统计量")

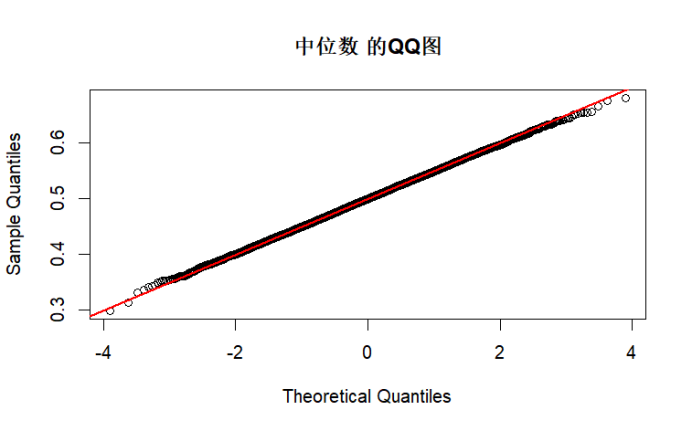
test_normality(sample_median, "中位数")

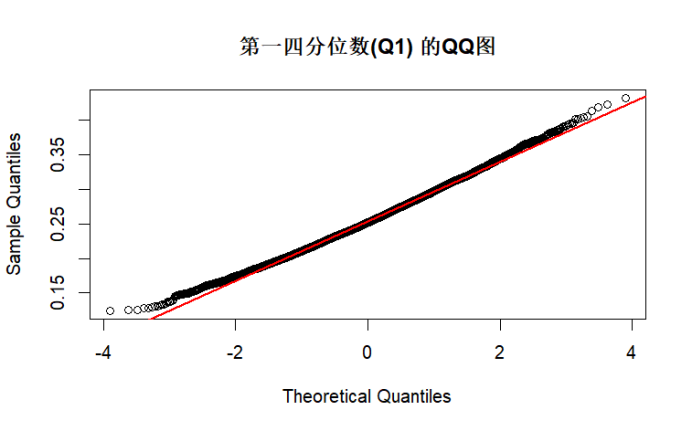
test_normality(sample_q1, "第一四分位数(Q1)")

test_normality(sample_q3, "第三四分位数(Q3)")

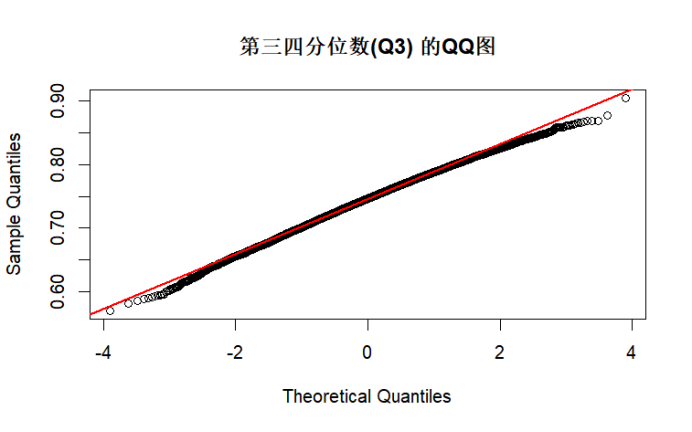
综上所述，由K-S检验和QQ图结果可知，当n足够大时，根据中心极限定理，各统计量的渐进分布接近正态分布，K-S 检验 p 值较高，QQ 图点会更贴近直线。