111.二叉树的最小深度(二叉树算法题)
111.二叉树的最小深度
力扣题目链接(opens new window)
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
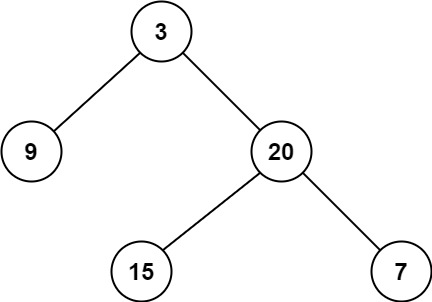
输入:root = [3,9,20,null,null,15,7] 输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
#思路
相对于 104.二叉树的最大深度 ,本题还也可以使用层序遍历的方式来解决,思路是一样的。
需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点。
/*** Definition for a binary tree node.* * public class TreeNode {* int val; // 节点的整数值* TreeNode left; // 指向左子节点的引用(指针),若无左子节点则为 null* TreeNode right; // 指向右子节点的引用(指针),若无右子节点则为 null* * // 默认构造函数:创建一个空节点(val 默认为 0)* TreeNode() {}* * // 构造函数:根据给定的值创建一个节点,左右子节点默认为 null* TreeNode(int val) { * this.val = val; * }* * // 构造函数:根据给定的值和左右子节点创建一个完整节点* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/class Solution {/*** 计算二叉树的最小深度。* * 二叉树的最小深度是从根节点到最近的叶子节点的最短路径上的节点数。* 叶子节点是指没有子节点的节点(即 left == null 且 right == null)。* * 算法使用层序遍历(广度优先搜索,BFS):* - 从根节点开始,逐层向下遍历。* - 一旦遇到第一个叶子节点,当前所在的层数就是最小深度。* - 因为 BFS 是按层进行的,所以第一个遇到的叶子节点一定是最浅的。* * 示例 1:* 输入:[3,9,20,null,null,15,7]* 3* / \* 9 20* / \* 15 7* 输出:2* 解释:从根节点 3 到叶子节点 9 的路径长度为 2,是最小深度。* * 示例 2:* 输入:[2,null,3,null,4,null,5,null,6]* 2* \* 3* \* 4* \* 5* \* 6* 输出:5* 解释:这是一条单边树,最小深度就是整条路径的长度。* * @param root 二叉树的根节点* @return 返回二叉树的最小深度(整数)*/public int minDepth(TreeNode root) {// 创建一个队列用于实现广度优先搜索(BFS)// 队列中存储待处理的树节点Queue<TreeNode> queue = new LinkedList<>();// 如果根节点为空,说明树为空,最小深度为 0if (root == null) return 0;// 将根节点加入队列,作为遍历的起点queue.offer(root);// 记录当前遍历的深度(层数),初始为 0int depth = 0;// 当队列不为空时,说明还有节点未处理(即还有层未遍历完)while (!queue.isEmpty()) {// 记录当前层的节点数量// 这个值决定了内层循环需要处理多少个节点int len = queue.size();// 每进入一层,深度加一depth++;// 遍历当前层的所有节点(共 len 个)for (int i = 0; i < len; i++) {// 从队列头部取出一个节点进行处理TreeNode temp = queue.poll();// 关键判断:如果当前节点是叶子节点(没有左右子节点)// 说明我们找到了从根到叶子的最短路径,直接返回当前深度if (temp.left == null && temp.right == null) {return depth;}// 如果当前节点有左子节点,则将其加入队列,供下一层处理if (temp.left != null) {queue.offer(temp.left);}// 如果当前节点有右子节点,则将其加入队列,供下一层处理if (temp.right != null) {queue.offer(temp.right);}}// 当前层的所有节点处理完毕// 队列中现在存储的是下一层的所有节点(如果有)}// 理论上不会执行到这里,因为只要有节点,最终一定会遇到叶子节点// 但为了语法完整,返回 depth(处理极端情况)return depth;}
}