强化学习（4）策略梯度与TD Learning

这里我们会聊一下策略梯度与TD Learning的关系

---

策略梯度与 TD Learning 的关系：Actor-Critic 架构

策略梯度和 TD Learning 并不是互相排斥的，它们的关系是互补的，并且它们最常在 Actor-Critic（演员-评论家） 架构中被同时使用。

简单来说：

1. 策略梯度（Policy Gradient） 负责 行动（Actor）：它直接学习 做什么动作 ($\pi$)。
2. TD Learning 负责 评估（Critic）：它学习 动作有多好 ($V$ 或 $Q$)。

1. 为什么需要结合？（TD Learning 解决策略梯度的问题）

单独使用策略梯度方法（如 REINFORCE）有一个致命的弱点：方差（Variance）太大。

策略梯度的更新公式通常需要使用完整的回报 $G_t$（即从当前时间步到回合结束的所有奖励的折扣总和）来衡量当前动作的好坏。

$$\text{梯度}\propto \mathbb{E}[{\nabla }_{\theta }\log \pi (A_t|S_t)\cdot G_t]$$

由于 $G_t$ 是一个随机变量（取决于后续所有状态和动作），它的波动性很大，这使得梯度估计很不稳定，导致训练收敛慢，甚至可能发散。

TD Learning 如何解决？

TD Learning 通过估计 价值函数 $V(s)$ 或 $Q(s,a)$，为策略梯度提供一个低方差的基准（Baseline）或优势估计（Advantage Estimate）。

$$\text{优势函数}A(s,a)=Q(s,a)-V(s)$$

在 Actor-Critic 架构中，策略梯度的更新公式变为：

$$\text{梯度}\propto \mathbb{E}[{\nabla }_{\theta }\log \pi (A_t|S_t)\cdot A_t]$$

这里的 $A_t$ (优势函数)就是通过 TD Learning 实时计算和更新的。

• 价值函数 $V(s)$（由 Critic 学习）充当了期望基准：它告诉 Actor 在状态 $s$ 下平均能获得多少回报。
• 优势函数 $A(s,a)$：它告诉 Actor 采取动作 $a$ 比平均预期好多少。

将 $G_t$ 替换为 $A_t$，可以大幅减少梯度的方差，因为 TD 估计比完整的蒙特卡洛回报 $G_t$ 稳定得多，从而使训练更稳定、更快速。

2. Actor-Critic 架构的工作流

现代高效的 RL 算法（如 A2C, A3C, PPO）都是基于这个思想：

暂时没有了解到GRPO等更先进的算法，以后补充

角色	学习对象	学习方法	TD Learning 的作用
Actor (演员)	策略 $\pi (a|s)$：决定如何行动。	策略梯度	利用 Critic 提供的 优势函数，指导策略朝更有利的动作方向更新。
Critic (评论家)	价值函数 $V(s)$：评估当前状态有多好。	TD Learning	使用 TD 误差来更新 $V(s)$ 的估计，确保对优势函数的评估是准确的。

所以Critic（TD Learning）通过不断学习和提供准确的价值评估，来指导 **Actor（策略梯度）**进行高效且稳定的策略改进。

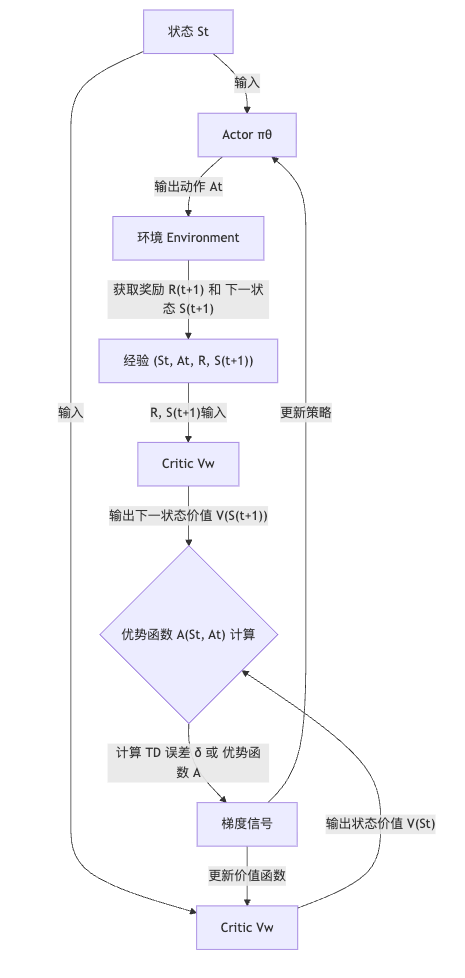
整个学习过程在一个连续的循环中进行：

步骤	角色	行动	关系与 TD Learning
1. 观测与输入	环境 & Actor/Critic	智能体观测到当前状态 St，并将 St 输入给 Actor ($\pi$) 和 Critic (V) 两个网络。	起始
2. 决策 (Actor)	Actor (${\pi }_{\theta }$)	根据策略 $\pi$ 输出动作 At。	策略梯度的实现。
3. 评估 (Critic)	Critic ($V_w$)	根据当前状态 St 输出状态价值的估计 V(St)。	TD 学习的估计值。
4. 交互与反馈	环境	执行动作 At，环境返回即时奖励 Rt+1 和下一状态 St+1。	经验数据的获取。
5. 计算 TD 目标	Critic (再次)	将 $S_{t+1}$ 输入 Critic，得到 $V(S_{t+1})$ 的估计。	准备计算 TD 目标。
6. 计算误差信号	TD Learning	计算 TD 误差 (δt)，这也是 Critic 的损失函数：	$\delta t=R_{t+1}+\gamma \cdot V(S_{t+1})-V(S_t)$	TD 学习的核心。
7. 策略更新	Actor (${\pi }_{\theta }$)	Actor 使用 TD 误差 δt（通常作为优势函数 At 的近似）来更新其策略参数 θ。$$\nabla \theta \propto {\delta }_t\cdot \nabla \log \pi (A_t|S_t)$$
8. 价值更新	Critic ($V_w$)	Critic 使用 TD 误差 ${\delta }_t$ 来更新其价值网络 V 的参数 w，使其对 $V(S_t)$ 的估计更准确。	TD 学习的更新，确保 Critic 评价更精确。

核心理解：双向反馈

1. Critic 驱动 Actor： Critic 的输出 δt 直接告诉 Actor：“你这次的动作 At 比预期的好/坏了 δt 这么多！” Actor 根据这个准确的反馈调整策略，而不是依靠波动性大的完整回报 Gt。
2. Actor 驱动 Critic： Actor 的探索会产生新的经验，Critic 利用这些新经验不断修正其 V(s) 估计，从而使自己成为一个更准确的“评论家”，为 Actor 提供更好的指导。

这就是 Actor-Critic 架构高效且稳定的原因：策略梯度负责探索，TD 学习负责稳定评估。