Python 数学公式构建海洋不明生物（好像是水母）动画 - 傅里叶合成模拟复杂波形

Python 数学公式构建海洋不明生物（好像是水母）动画 - 傅里叶合成模拟复杂波形

flyfish

Python 数学公式构建海洋不明生物（好像是水母）动画 - 简谐振动
效果展示与源码

可以先欣赏下海洋不明生物（好像是水母）的动画

代码绘制效果如下图

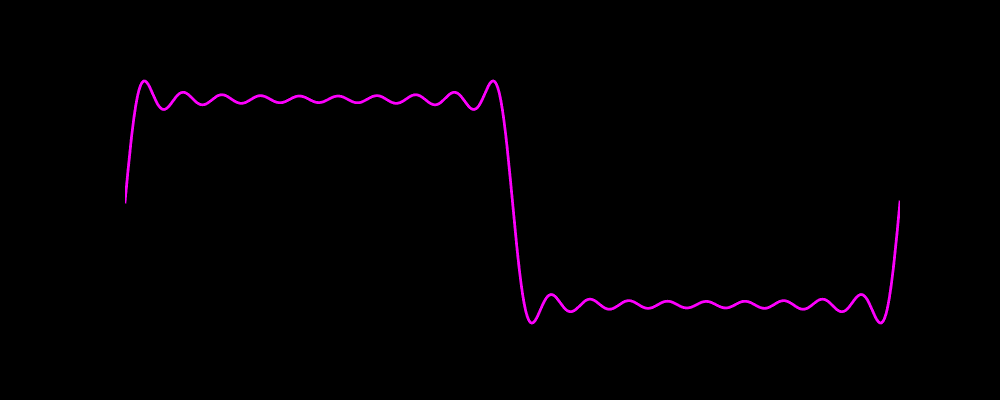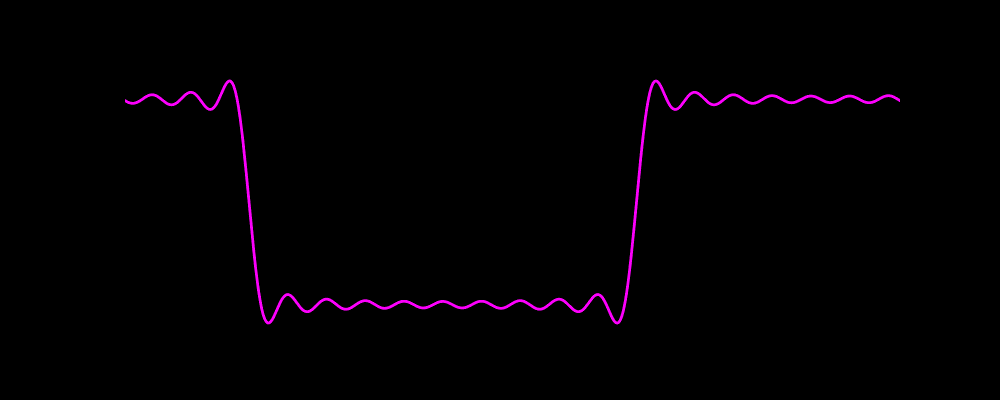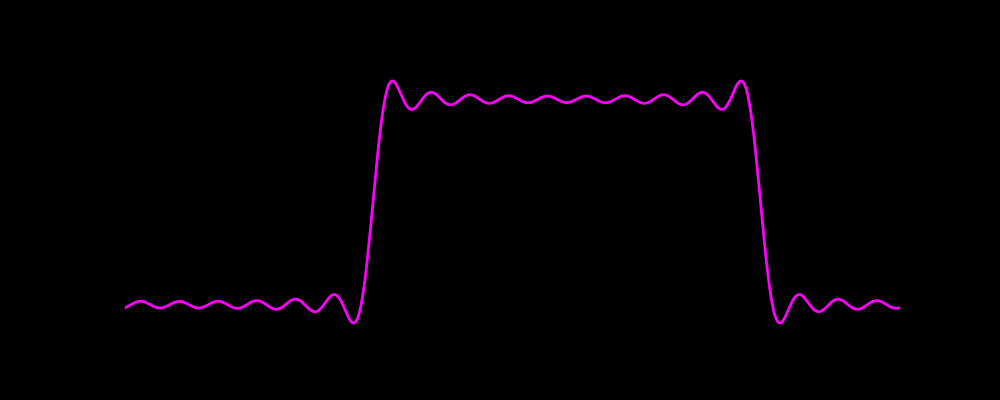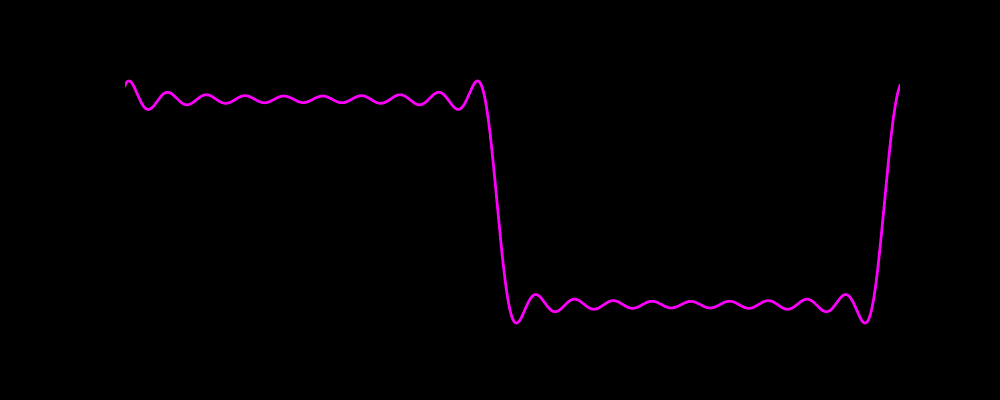
一、傅里叶的发现：所有周期波，都是简谐波的“拼图”

1807年，法国数学家傅里叶在研究热传导问题时，提出了一个颠覆认知的观点（后来发展为傅里叶定理）：
任何满足一定条件的周期函数（比如方波、三角波、锯齿波，甚至自然界的海浪、声波），都可以分解为无限多个不同频率、不同振幅的正弦波（或余弦波）的叠加。

这句话里藏着两个关键方向，也是傅里叶分析的两大核心：

• 傅里叶分解（Fourier Decomposition）：把复杂的周期波“拆碎”成一个个简单的正弦波（叫“谐波”）。
• 傅里叶合成（Fourier Synthesis）：把拆出来的谐波“拼回去”，重新组成原来的复杂波形（代码里做的就是这个）。

打个比方：如果把复杂波形比作“一道宫保鸡丁”，那么傅里叶分解就是“分析这道菜里有鸡丁、花生、辣椒、糖、盐等食材”；傅里叶合成就是“用这些食材按比例混合，重新做出宫保鸡丁”。而这里的“食材”，就是我们之前反复聊过的简谐波。

二、傅里叶合成的基础：3个核心概念

在讲“怎么合成”之前，得先明确3个关键术语——它们是“拼波形”的“食材说明书”，也是代码逻辑的核心。

1. 周期函数：“重复出现”是前提

傅里叶合成只针对周期函数（波形在时间或空间上重复出现），比如代码里的“方波”：它的形状是“水平→垂直跳变→水平→垂直跳变”，每隔固定距离（叫“周期$\lambda$”）就重复一次。

自然界的海浪、声波、交流电波形，本质都是周期函数（或近似周期函数），所以都能用傅里叶合成模拟。

2. 基波与谐波：“基础食材”和“调味食材”

分解复杂波形时，会得到一组“有规律的正弦波”，按频率分为两类：

• 基波（Fundamental Wave）：频率最低的那个正弦波，它的频率叫“基频（$f_0$）”，周期和原复杂波形的周期完全一致。它是构成复杂波形的“骨架”。
• 谐波（Harmonics）：频率是基频整数倍的正弦波（频率=$2f_0$、$3f_0$、$4f_0$…），分别叫“2次谐波、3次谐波、4次谐波…”。它们是给“骨架”添细节的“调味剂”。

举个例子：代码里模拟的“方波”，其基频是$f_0$（对应谐波阶数$n=1$），而参与合成的只有奇数谐波（$n=1$、$3$、$5$…）——这是方波的傅里叶级数特性（偶数谐波的振幅为0，所以不用加）。

3. 振幅谱：“食材的用量比例”

不同谐波的“重要性”不一样，用“振幅”来衡量——振幅越大，这个谐波对最终波形的影响越明显。把“谐波阶数”和“对应振幅”列出来，就是“振幅谱”，它相当于“菜谱里的食材用量表”。

以代码里的方波为例，其振幅谱有明确的数学规律：
第$n$次谐波的振幅 $A_n=\frac{4}{\pi }\times \frac{1}{n}\times A_{\text{base}}$
（$n$只能是奇数，比如$n=1$时$A_1=\frac{4}{\pi }\times A_{\text{base}}$；$n=3$时$A_3=\frac{4}{\pi }\times \frac{1}{3}\times A_{\text{base}}$，以此类推）

这个规律的特点是：谐波阶数越高（$n$越大），振幅越小——意味着“高次谐波”只影响波形的细节（比如方波的“棱角”），而“低次谐波”决定波形的整体轮廓。

三、傅里叶合成的原理：手把手教你“拼出方波”

傅里叶合成的逻辑很简单：按振幅谱的比例，把基波和所有谐波“叠加”起来。下面结合代码，一步步看“如何从正弦波拼出方波”。

1. 第一步：确定“合成公式”（方波的傅里叶级数）

根据傅里叶定理，方波的“合成公式”（傅里叶级数）是：
$$y(x,t)=\frac{4}{\pi }\sum _{n=1,3,5,...}^{\infty }\frac{1}{n}{A}_{\text{base}}\sin \left(n(kx-\omega t)\right)$$

公式里的每个部分，都对应代码的逻辑：

• $\frac{4}{\pi }$：方波傅里叶级数的“固定系数”（由数学推导得出，确保合成波形的振幅符合预期）；
• $n$：谐波阶数（代码里用i表示，只取奇数：range(1, num_harmonics*2, 2)）；
• $\frac{1}{n}$：高次谐波的振幅衰减因子（$n$越大，振幅越小）；
• $A_{\text{base}}$：基础振幅（代码里的amplitude_base，控制整体波形的高度）；
• $\sin (n(kx-\omega t))$：第$n$次谐波的“简谐波行波”（$kx-\omega t$是行波的标准形式，-wave_speed*t对应代码里的传播项，让波形向右移动）。

2. 第二步：从“1个谐波”到“多个谐波”的叠加过程

傅里叶合成的精髓在于“叠加越多，越接近理想波形”，我们用代码里的参数（num_harmonics=10，即取前10个奇数谐波：$n=1$、$3$、…、$19$）来拆解这个过程：

（1）只加基波（$n=1$）：就是一条普通正弦波

当num_harmonics=1时，合成公式简化为：
$$y(x,t)=\frac{4}{\pi }{A}_{\text{base}}\sin (kx-\omega t)$$
此时波形就是一条光滑的正弦曲线，和方波完全不像——这说明“只靠骨架（基波），做不出复杂波形”。

（2）加基波+3次谐波（$n=1+3$）：波形开始“变方”

叠加$n=1$和$n=3$的谐波后：
$$y(x,t)=\frac{4}{\pi }{A}_{\text{base}}\left[\sin (kx-\omega t)+\frac{1}{3}\sin (3(kx-\omega t))\right]$$
此时正弦波的“波峰”和“波谷”开始变平，因为3次谐波的“小波动”填补了基波的平滑部分，轮廓开始向方波靠拢。

（3）加更多高次谐波（$n=1+3+5+\dots +19$）：逼近理想方波

随着谐波数量增加（比如代码里的10个奇数谐波），高次谐波的“高频小波动”会不断修正波形：波峰/波谷越来越平，边缘的“跳变”越来越陡，最终形成非常接近理想方波的形状。

但这里有个有趣的现象——吉布斯现象（Gibbs Phenomenon）：即使加了很多谐波，波形的“跳变边缘”还是会有微小的“过冲”（比理想方波的峰值略高一点，再快速回落），这是有限谐波叠加的必然结果（无限谐波叠加才能完全消除）。

3. 第三步：让合成波“动起来”（行波传播）

代码里的波形不是静止的，而是向右传播的——这是因为在每个谐波的正弦函数里加了“传播项”：n*(x - wave_speed*t)。

这个传播项的逻辑和我们之前讲的“行波公式”一致：

• 当时间$t$增加时，x - wave_speed*t的值需要更大的$x$才能保持不变（比如$t=0$时，某点在$x=0$处；$t=1$时，该点移动到KaTeX parse error: Expected 'EOF', got '_' at position 13: x=\text{wave_̲speed}处），所以整个波形会沿$x$轴正方向移动，速度就是wave_speed。

每个谐波都以相同的速度传播（因为wave_speed是统一的），所以叠加后的整体波形也会同步传播，不会因为谐波不同而“散架”。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter# 参数设置（可调整）
amplitude_base = 1.0    # 基础振幅（用于所有谐波）
wave_speed = 2.0        # 整体波速（传播速度）
num_harmonics = 10      # 谐波数量（越多越接近复杂波形，如方波；建议5-20）
num_points = 500        # x轴点数（分辨率，提高以获得更平滑曲线）
animation_frames = 100  # 动画帧数
interval = 150           # 每帧间隔（ms）# 创建图形
fig, ax = plt.subplots(figsize=(10, 4), facecolor='black')
ax.set_facecolor('black')
ax.set_xlim(0, 2 * np.pi)
ax.set_ylim(-amplitude_base * 1.5, amplitude_base * 1.5)  # 调整范围以容纳叠加波
ax.axis('off')  # 隐藏轴线，纯视觉效果# x 数据（固定）
x = np.linspace(0, 2 * np.pi, num_points)# 初始波形数据（开始时全零或初始叠加）
line, = ax.plot(x, np.zeros_like(x), color='magenta', lw=2)  # 使用品红色以突出复杂性# 傅里叶合成函数：模拟方波（square wave）的傅里叶级数
# 方波的傅里叶级数：y = (4/π) * sum_{n=1,3,5,...} (1/n) * sin(n * (kx - ωt))
# 这里 n 为奇数谐波 (1,3,5,...), k=1 (基础波数)
def fourier_square_wave(x, t, num_harmonics):y = np.zeros_like(x)for i in range(1, num_harmonics * 2, 2):  # 只取奇数谐波：1,3,5,...freq = i  # 频率倍数amp = (4 / np.pi) * (1 / i) * amplitude_base  # 振幅衰减y += amp * np.sin(freq * (x - wave_speed * t))  # 叠加行波形式return y# 更新函数：每帧计算新波形（傅里叶叠加的行波）
def update(frame):t = frame * (2 * np.pi / animation_frames)  # 时间累积（无speed缩放，因为已在sin中）y = fourier_square_wave(x, t, num_harmonics)line.set_ydata(y)return line,# 创建动画
ani = FuncAnimation(fig, update, frames=animation_frames, interval=interval, blit=True)# 保存为 GIF（使用 PillowWriter）
writer = PillowWriter(fps=1000 / interval)
ani.save('fourier_wave_animation.gif', writer=writer, dpi=100)print("傅里叶合成波浪动画已保存为 fourier_wave_animation.gif")
plt.close(fig)  # 关闭图形，释放资源