435. 无重叠区间
目录
题目链接:
题目:
解题思路:
代码:
总结:
题目链接:
435. 无重叠区间 - 力扣(LeetCode)
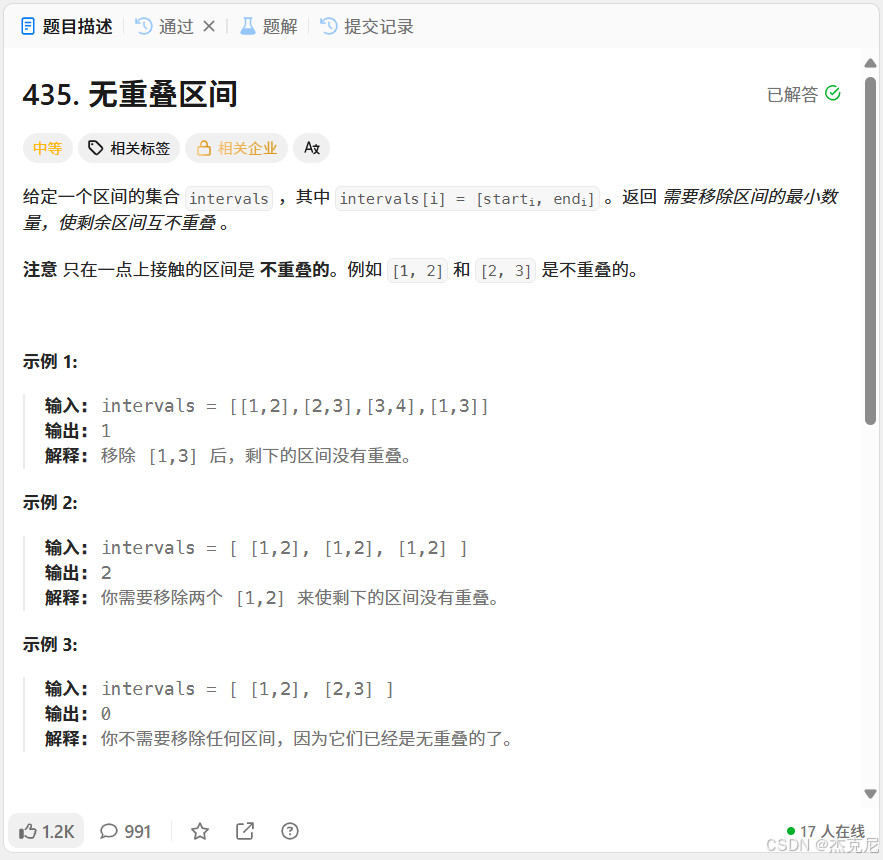
题目:
解题思路:
根据左侧排序,然后当前的集合的左侧和之前的右侧比较即可,若不重复,就更改之前的记录即可,若重复,就选择当前集合的右侧和之前的右侧的最小值(因为要删去大范围),并进行累加即可
代码:
class Solution {public int eraseOverlapIntervals(int[][] intervals) {if(intervals.length==1) return 0;Arrays.sort(intervals,(a,b)->{return a[0]-b[0];});int end=intervals[0][1];int res=0;for(int i=1;i<intervals.length;i++){if(end<=intervals[i][0]){end=intervals[i][1];}else{res++;end=Math.min(intervals[i][1],end);}}return res;}
}
【算法详解】无重叠区间:贪心算法的区间调度应用
1. 引言
大家好,今天我们来探讨一道非常经典的贪心算法题 ——“无重叠区间”。这道题与 “用最少数量的箭引爆气球” 问题非常相似,都是区间调度问题的核心模型。通过解决这道题,我们可以进一步加深对贪心算法在处理区间问题时的理解和应用。
我将带领大家从问题本身出发,一步步拆解,找到其内在规律,并最终理解为什么这个解法能够高效地找到最优解。
2. 问题描述
我们先来看一下题目:
给定一个区间的集合 intervals,其中 intervals[i] = [starti, endi]。返回需要移除区间的最小数量,使剩余区间互不重叠。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]输出: 1
解释:移除 [1,3] 后,剩下的区间 [[1,2],[2,3],[3,4]] 互不重叠。
示例 2:
输入: intervals = [[1,2],[1,2],[1,2]]输出: 2
解释:我们需要移除两个 [1,2] 才能使剩下的区间 [[1,2]] 互不重叠。
示例 3:
输入: intervals = [[1,2],[2,3]]输出: 0
解释:不需要移除任何区间,因为它们已经互不重叠。
3. 问题分析与核心难点
拿到这个问题,我们首先会思考:要移除最少的区间,等价于要保留最多的不重叠区间。所以,问题可以转化为 “在所有区间中,最多能选出多少个互不重叠的区间?”,然后用总区间数减去这个最大值,就是需要移除的最小数量。
核心难点在于: 如何选择保留哪些区间,才能保证它们互不重叠,并且数量最多?
这是一个典型的区间调度问题 (Interval Scheduling),而解决此类问题的最优策略通常是贪心算法。
4. 贪心策略的选择与证明
贪心算法的核心是在每一步决策时,都采取当前看起来最优的选择,从而希望由局部最优解最终导出全局最优解。
那么,对于这个问题,我们的 “局部最优” 选择是什么呢?我们应该按什么顺序来考虑区间,又该如何选择保留哪一个区间呢?
4.1 策略选择:按区间的右边界排序
经过对问题的分析,最有效的贪心策略是:优先保留那些结束得最早的区间。
为什么是右边界?
如果我们选择一个结束得很早的区间,那么它留给其他区间的 “空间” 就会更大,从而有更大的可能性去容纳更多不重叠的区间。
相反,如果我们选择一个结束得很晚的区间,它会占用大量的空间,可能导致后续很多区间都无法被选择。
举个例子:
假设我们有三个区间:A [1, 4],B [2, 3],C [5, 6]。
如果我们不排序,直接选择 A [1, 4],那么我们接下来只能选择 C [5, 6],总共保留 2 个区间。
如果我们按照右边界升序排序,顺序是 B [2, 3],A [1, 4],C [5, 6]。
我们优先选择 B [2, 3](因为它结束得最早)。
接下来,我们在 B 之后寻找不重叠的区间,可以选择 C [5, 6]。
总共也保留了 2 个区间。
在这个简单的例子中,两种选择结果一样。我们再看一个更能体现策略优势的例子:
假设我们有三个区间:A [1, 100],B [2, 3],C [4, 5]。
错误策略:如果我们选择了 A [1, 100],那么 B 和 C 都无法被选择,最终只能保留 1 个区间。
正确策略(按右边界排序):排序后顺序是 B [2, 3],C [4, 5],A [1, 100]。
我们优先选择 B [2, 3]。
接下来,我们选择 C [4, 5](它与 B 不重叠)。
最终我们保留了 2 个区间,显然优于错误策略。
这个例子清晰地展示了优先选择结束得最早的区间可以为后续选择留下更多机会,从而可能得到更优的解。
4.2 算法步骤
基于以上策略,我们可以制定出详细的算法步骤:
排序:将所有区间按照其右边界 endi 的升序进行排序。
初始化:
记录需要移除的区间数量 count,初始化为 0。
记录上一个被选中的区间的右边界 lastEnd,初始化为第一个区间的右边界 intervals[0][1]。
遍历与选择:
从第二个区间开始,遍历排序后的所有区间 intervals[i]。
对于每个区间 intervals[i],比较它的左边界 intervals[i][0] 与 lastEnd:
情况一:不重叠。如果 intervals[i][0] >= lastEnd,说明当前区间与上一个被选中的区间不重叠。我们可以保留这个区间。
更新 lastEnd 为当前区间的右边界 intervals[i][1]。
情况二:重叠。如果 intervals[i][0] < lastEnd,说明当前区间与上一个被选中的区间重叠了。根据我们的贪心策略,我们应该移除当前这个区间,因为它结束得更晚(或者一样晚),会占用更多空间。
将需要移除的区间数量 count 加一。
注意:我们不更新 lastEnd,因为我们选择保留的是上一个结束得更早的区间。
4.3 算法证明(为什么这个解法是正确的?)
我们可以用反证法来证明这个算法的正确性。
假设: 存在一个最优解 OPT,它保留的不重叠区间数量比我们的贪心算法解 GREEDY 更多。
我们来分析一下 OPT 和 GREEDY 的区别:
考虑第一个区间。在 GREEDY 算法中,我们选择了所有区间中右边界最早的那个区间,记为 g1。
在 OPT 解中,它选择的第一个区间记为 o1。
因为 g1 是所有区间中右边界最早的,所以 g1 的右边界 end(g1) 必然小于或等于 o1 的右边界 end(o1)。
关键一步:我们将 OPT 解中的第一个区间 o1 替换为 g1。
这个替换是安全的。因为 end(g1) <= end(o1),所以任何在 o1 之后能被 OPT 解选中的区间,也必然能在 g1 之后被选中(它们的左边界都大于 end(o1),自然也大于 end(g1))。
替换之后,OPT 解中保留的区间数量不会减少。
我们可以对后续的区间重复这个过程。每次都可以将 OPT 解中对应步骤的区间,替换为 GREEDY 算法选择的区间,而不会减少保留的区间总数。
最终,我们可以将 OPT 解完全转换成 GREEDY 解,且两者保留的区间数量相同。
这与我们最初的假设(OPT 保留的区间更多)相矛盾。因此,我们的贪心算法解 GREEDY 必然是最优解。
5. 代码详解
现在,我们来逐行解析你提供的 Java 代码。
java
运行
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
// 特殊情况处理:如果只有一个区间,不可能重叠,无需移除任何区间
if (intervals.length == 1) {
return 0;
}
// 1. 排序
// 按照区间的右边界升序排序
Arrays.sort(intervals, (a, b) -> {
return a[1] - b[1];
});
// 2. 初始化
int count = 0; // 需要移除的区间数量,初始为0
// 记录上一个被选中的区间的右边界,初始化为第一个区间的右边界
int end = intervals[0][1];
// 3. 遍历与选择
// 从第二个区间开始遍历
for (int i = 1; i < intervals.length; i++) {
// 情况一:当前区间与上一个被选中的区间不重叠
if (end <= intervals[i][0]) {
// 更新上一个被选中的区间的右边界为当前区间的右边界
end = intervals[i][1];
}
// 情况二:当前区间与上一个被选中的区间重叠
else {
// 我们选择移除当前这个区间
count++;
// 关键:我们不更新 end,因为我们保留的是上一个结束得更早的区间
// 代码中 end = Math.min(end, intervals[i][1]); 是多余的,因为 intervals[i][1] >= end
// 因为数组已经按右边界排序,所以 intervals[i][1] >= intervals[i-1][1] >= ... >= end
}
}
// 返回需要移除的区间总数
return count;
}
}
代码逻辑回顾与分析
你提供的这段代码,完美地实现了我们上面讨论的贪心算法。
Arrays.sort(intervals, (a, b) -> { return a[1] - b[1]; });
这行代码是整个算法的基石。它正确地将区间按照右边界升序排序,为后续的贪心选择做好了准备。
int count = 0; int end = intervals[0][1];
count 用于计数需要移除的区间。
end 用于追踪我们保留下来的最后一个区间的右边界。这是贪心选择的关键变量。
for 循环
循环开始:for (int i = 1; i < intervals.length; i++)。从索引 1 开始,因为我们已经将索引 0 的区间默认为第一个被保留的区间。
不重叠判断:if (end <= intervals[i][0])。这是判断当前区间 intervals[i] 是否可以被保留的条件。如果可以,我们就更新 end。
重叠处理:else。如果发生重叠,根据策略,我们移除当前区间 intervals[i],所以 count++。你代码中的 end = Math.min(end, intervals[i][1]); 这一行实际上是多余的,因为数组已经按右边界排序,intervals[i][1] 的值一定大于或等于 end 的值,所以 Math.min(end, intervals[i][1]) 的结果永远是 end。
一个小问题与修正
如前所述,end = Math.min(end, intervals[i][1]); 这行代码是冗余的,可以安全地删除,使代码更简洁、意图更明确。
优化后的代码如下:
java
运行
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
// 更全面的特殊情况处理
if (intervals == null || intervals.length == 0) {
return 0;
}
// 1. 按照右边界升序排序
Arrays.sort(intervals, (a, b) -> a[1] - b[1]);
// 2. 初始化
int count = 0;
int lastEnd = intervals[0][1];
// 3. 遍历与选择
for (int i = 1; i < intervals.length; i++) {
// 如果当前区间的左边界小于上一个保留区间的右边界,说明重叠
if (intervals[i][0] < lastEnd) {
// 重叠,移除当前区间
count++;
} else {
// 不重叠,保留当前区间,并更新上一个保留区间的右边界
lastEnd = intervals[i][1];
}
}
return count;
}
}
这个优化版本不仅移除了冗余代码,还将 if/else 的逻辑进行了互换,使得对重叠情况的处理更直接,代码可读性更高。
6. 复杂度分析
时间复杂度:O(N log N)
算法的主要耗时在于对 intervals 数组的排序,其时间复杂度为 O(N log N)。
后续的遍历过程是线性的,时间复杂度为 O(N)。
总时间复杂度为 O(N log N + N),最终简化为 O(N log N)。
空间复杂度:O(log N) 或 O(N)
空间复杂度主要取决于排序算法的实现。在 Java 中,Arrays.sort() 对于对象数组(如 int[][])使用 Timsort 算法,其空间复杂度为 O(N)。
7. 总结与思考
这道题是贪心算法解决区间问题的又一个典范。它的巧妙之处在于:
找到正确的贪心策略:通过分析,我们确定了 “优先保留结束得最早的区间” 是一个能够导向全局最优解的局部最优策略。
清晰的算法逻辑:算法流程非常直观 —— 排序后,遍历并不断选择不重叠且结束得最早的区间,当遇到重叠时,就移除当前区间。
严谨的正确性证明:通过反证法,我们可以确信这个贪心策略不会错过任何最优解。
这个问题给我们的启示是:在处理区间相关的问题时,排序是一个非常强大的预处理步骤。通过选择合适的排序键(如左边界、右边界),往往能极大地简化问题,为贪心算法的应用铺平道路。
希望这篇详细的解析能帮助你彻底理解这道题,并掌握这类区间问题的通用解法!
总结:
本文介绍了使用贪心算法解决无重叠区间问题的思路。通过将所有区间按右边界排序,优先保留结束最早的区间,可以最大化保留不重叠区间的数量。代码实现首先排序,然后遍历比较当前区间左边界与上一个保留区间的右边界,统计需要移除的重叠区间数。该算法时间复杂度为O(NlogN),空间复杂度取决于排序实现。文章详细解释了贪心策略的正确性,并提供了优化后的代码示例。
