DDPM原理解析

1. DDPM原理

• 论文：DDPM: Denoising Diffusion Probabilistic Models

1.1 概述

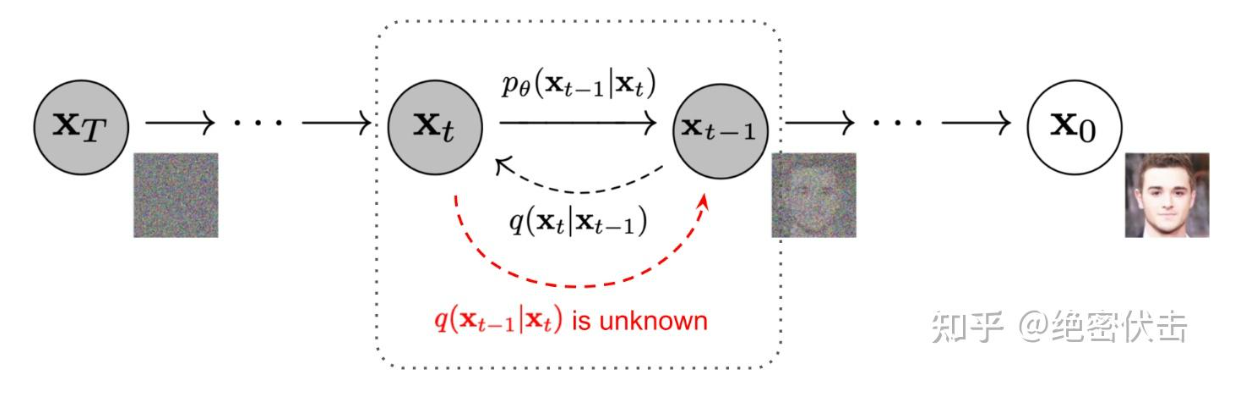
DDPM包括两个过程：前向过程（forward process）和反向过程（reverse process），其中前向过程又称为扩散过程（diffusion process），如下图所示。无论是前向过程还是反向过程都是一个参数化的马尔可夫链（Markov chain），其中反向过程可以用来生成图片。下图中，由高斯随机噪声$X_T$生成原始图片$X_0$为反向过程，反之为前向过程。

1.2 Forward(扩散过程)

一句话概括，前向过程就是对原始图片$X_0$不断加高斯噪声最后生成随机噪声$X_T$的过程，如下图所示。

由$X_{t-1}$到$X_t$表示为：
$${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}\text{\hspace{1em}(1)}$$

# 生成[b, 1, 1, 1]的tensor, 完成“信号衰减 + 噪声注入”
def extract(a, t, x_shape):b, *_ = t.shapeout = a.gather(-1, t)return out.reshape(b, *((1,) * (len(x_shape) - 1)))def perturb_x(self, x, t, noise):# DDPM 前向加噪的公式# self.sqrt_alphas_cumprod = np.sqrt(alphas_cumprod)# self.sqrt_one_minus_alphas_cumprod = np.sqrt(1 - alphas_cumprod)return (extract(self.sqrt_alphas_cumprod, t,  x.shape) * x +extract(self.sqrt_one_minus_alphas_cumprod, t, x.shape) * noise)

其中${\alpha }_t$是一个很小值的超参数， ${\mathbf{ϵ}}_{\mathbf{t}-1}\sim \mathbf{N}\left(0,1\right)$是高斯噪声。由公式（1）推导，最终可以得到$X_0$到$X_t$​的公式，表示如下：
$${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ}\text{\hspace{1em}(2)}$$
其中$\begin{array}{l}{\bar{\mathbf{\alpha }}}_{\mathbf{t}}={\prod }_{\mathbf{i}=1}^{\mathbf{t}}{\mathbf{\alpha }}_{\mathbf{i}},\mathbf{ϵ}\sim \mathbf{N}\left(0,1\right)\end{array}$也是一个高斯噪声。有了公式（2），便可以由输入图片直接生成随机噪声$X_t$。

1.3 Backward(去噪过程)

前向过程是将原始图片变成随机噪声，而反向过程就是通过预测噪声$ϵ$，将随机噪声$X_T$逐步还原为原始图片$X_0$​，如下图所示。

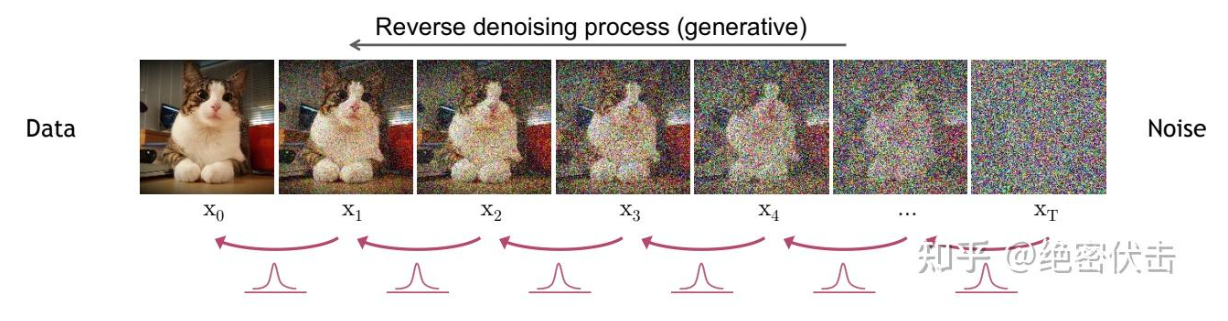
反向过程公式表示如下：
$${\mathbf{x}}_{t\text{–}1}=\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right))+{\sigma }_t\mathbf{z}\text{\hspace{1em}(3)}$$
其中${ϵ}_{\theta }$是噪声估计函数，用于估计真实噪声$ϵ$，$\theta$是模型训练的参数，$\mathbf{z}\sim N\left(0,1\right)$，${\sigma }_t\mathbf{z}$表示的是预测噪声和真实噪声的误差。DDPM的关键就是训练噪声估计模型${\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)$，用于估计真实的噪声$ϵ$​。

estimated_noise = self.model(perturbed_x, t, y)

def remove_noise(self, x, t, y, use_ema=True):# self.remove_noise_coeff = betas / np.sqrt(1 - alphas_cumprod))if use_ema:return ((x - extract(self.remove_noise_coeff, t, x.shape) * self.ema_model(x, t, y)) *extract(self.reciprocal_sqrt_alphas, t, x.shape))else:return ((x - extract(self.remove_noise_coeff, t, x.shape) * self.model(x, t, y)) *extract(self.reciprocal_sqrt_alphas, t, x.shape))
# 去噪
def sample(self, batch_size, device, y=None, use_ema=True):if y is not None and batch_size != len(y):raise ValueError("sample batch size different from length of given y")# 生成一个随机的噪声图像 shape为(batch_size, img_channels, img_size[0], img_size[1])x = torch.randn(batch_size, self.img_channels, *self.img_size, device=device)for t in range(self.num_timesteps - 1, -1, -1):# 生成一个形状为(batch_size,)的tensor, 每个元素都是tt_batch = torch.tensor([t], device=device).repeat(batch_size)x = self.remove_noise(x, t_batch, y, use_ema)if t > 0:x += extract(self.sigma, t_batch, x.shape) * torch.randn_like(x) # 预测噪声和真实噪声的误差return x.cpu().detach()

1.4 Training

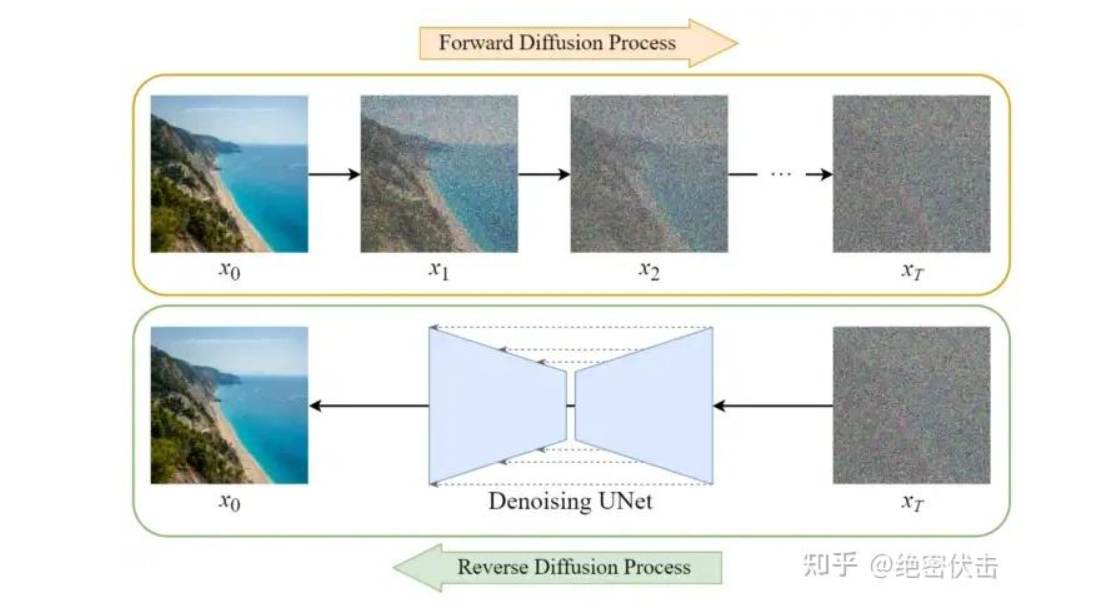
Diffusion模型的训练可以分为两个部分：

1. 前向扩散过程（Forward Diffusion Process）→ 图片中添加噪声
2. 反向扩散过程（Reverse Diffusion Process） → 去除图片中的噪声

前面提到DDPM的关键是训练噪声估计模型${\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)$，用于估计$ϵ$​，那么损失函数可以使用MSE误差，表示如下：
$$Loss={\Vert ϵ-{ϵ}_{\theta }\left({\mathbf{x}}_t,t\right)\Vert }^2={\Vert ϵ-{ϵ}_{\theta }\left({\sqrt{\bar{\alpha }}}_t{\mathbf{x}}_{t-1}+\sqrt{1-{\bar{\alpha }}_t}ϵ,t\right)\Vert }^2\text{\hspace{1em}(4)}$$
整个训练过程可以表示如下：

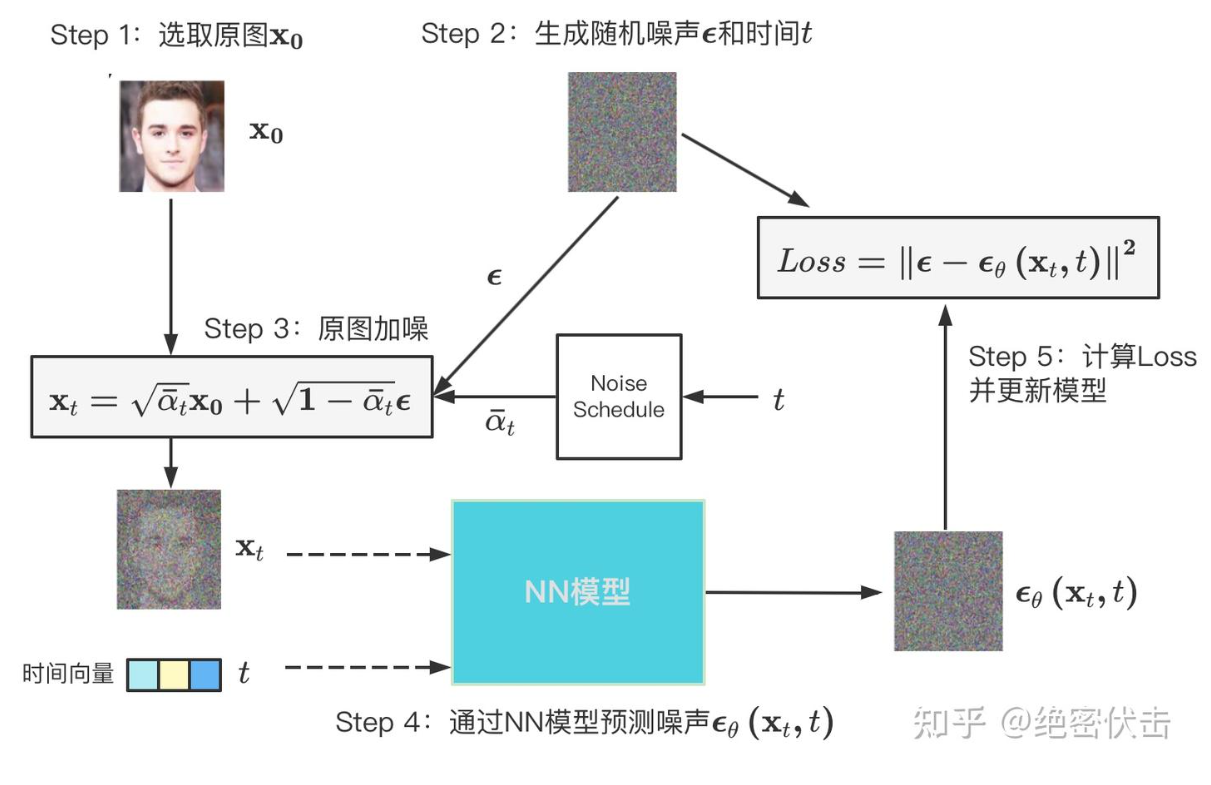
在每一轮的训练过程中，包含以下内容：

1. 每一个训练样本选择一个随机时间步长t
2. 将time step t对应的高斯噪声应用到图片中
3. 将time step转化为对应embedding

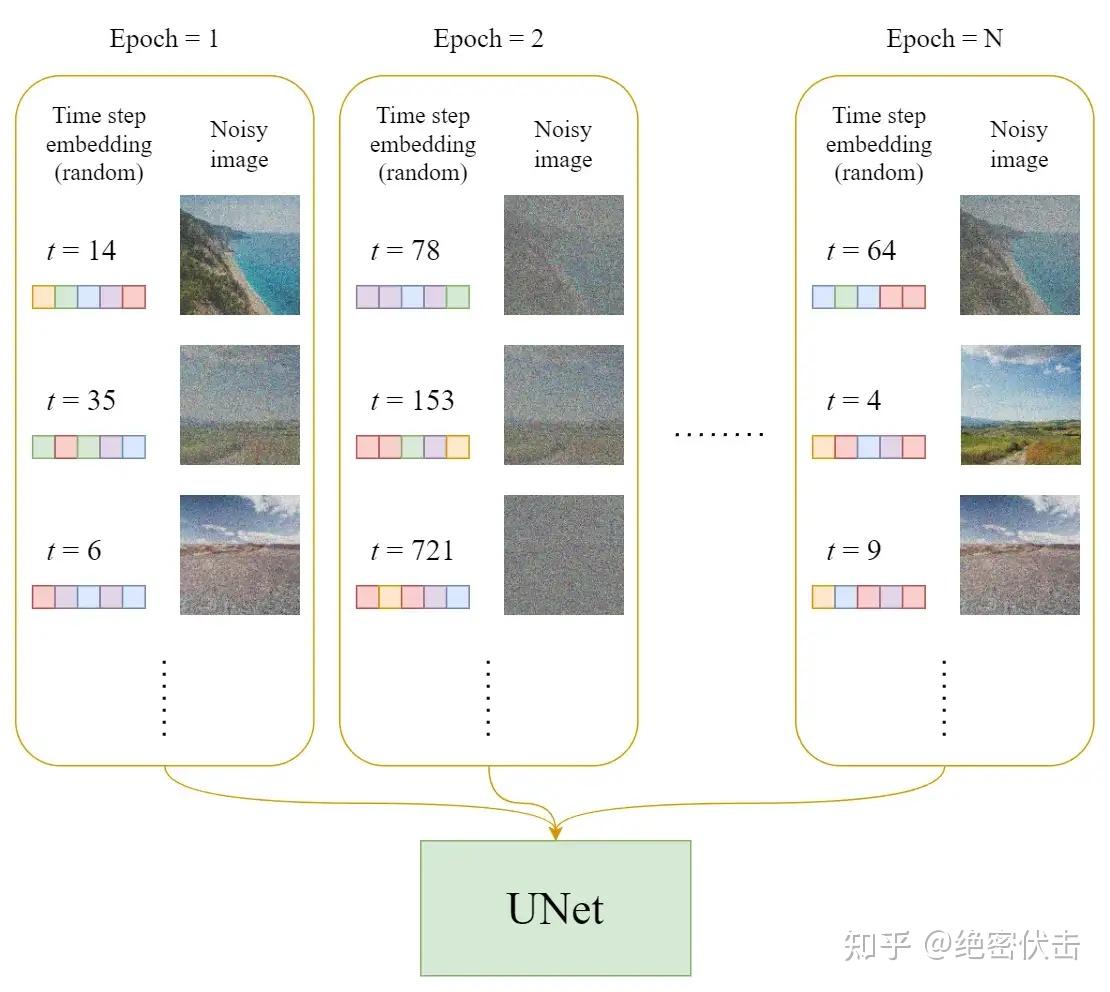
下面是每一轮详细的训练过程：

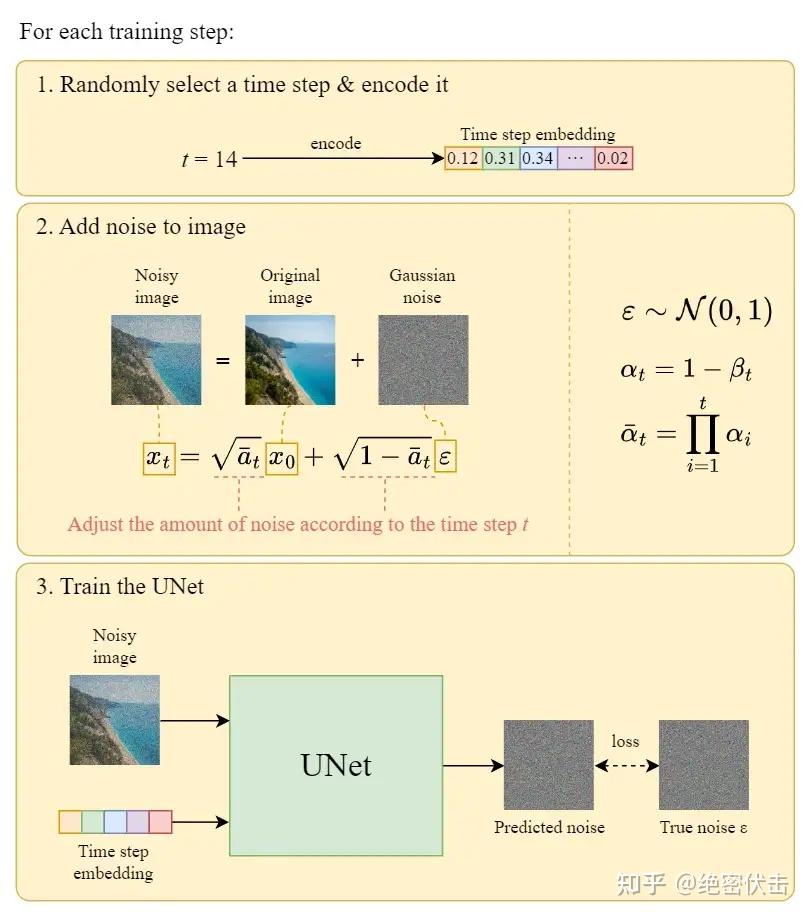
# 对时间轴输入的全连接层
self.time_mlp = nn.Sequential(PositionalEmbedding(base_channels, time_emb_scale),nn.Linear(base_channels, time_emb_dim),SiLU(),nn.Linear(time_emb_dim, time_emb_dim),
) if time_emb_dim is not None else None
# 对时间time_emb做一个全连接，施加在通道上
if self.time_bias is not None:if time_emb is None:raise ValueError("time conditioning was specified but time_emb is not passed")out += self.time_bias(self.activation(time_emb))[:, :, None, None]

1.5 Generation

在得到预估噪声${\mathbf{ϵ}}_{\theta }\left({\mathbf{x}}_t,t\right)$后，就可以按公式（3）逐步得到最终的图片$X_0$​，整个过程表示如下：

下图的Sample a Gaussian表示生成随机高斯噪声，Iteratively denoise the image表示反向扩散过程，如何一步步从高斯噪声变成输出图片。可以看到最终生成的Denoised image非常清晰。

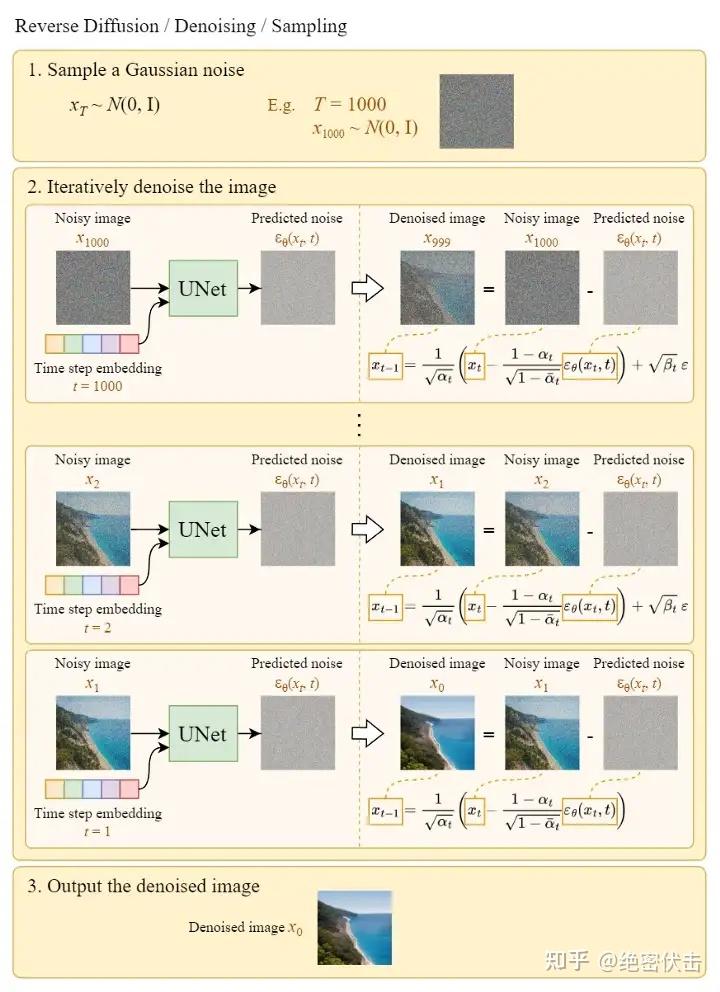
1.6 Problems

• UNet引入时间t，t是增长的还是随机的？

  • 引入时间步长t是为了模拟一个随时间逐渐增强的扰动过程。每个时间步长t代表一个扰动过程，从初始状态开始，通过多次应用噪声来逐渐改变图像的分布。因此，较小的t代表较弱的噪声扰动，而较大的t代表更强的噪声扰动。
  • DDPM 中的 UNet 都是共享参数的，那如何根据不同的输入生成不同的输出，最后从一个完全的一个随机噪声变成一个有意义的图片，这还是一个非常难的问题。我们希望这个 UNet 模型在刚开始的反向过程之中，它可以先生成一些物体的大体轮廓，随着扩散模型一点一点往前走，然后到最后快生成逼真图像的时候，这时候希望它学习到高频的一些特征信息。由于 UNet 都是共享参数，这时候就需要 time embedding 去提醒这个模型，我们现在走到哪一步了，现在输出是想要粗糙一点的，还是细致一点的。
  • t在训练过程是随机的每次训练中会从T∈[0, 1000]中均匀采样，在生成的时候在从1000逐渐降低到0，来模拟去噪过程。

• 时间t是如何编码的？

  #------------------------------------------#
  #   计算时间步长的位置嵌入。
  #   一半为sin，一半为cos。
  #------------------------------------------#
  class PositionalEmbedding(nn.Module):def __init__(self, dim, scale=1.0):super().__init__()assert dim % 2 == 0self.dim = dimself.scale = scaledef forward(self, x):device      = x.devicehalf_dim    = self.dim // 2emb = math.log(10000) / half_dimemb = torch.exp(torch.arange(half_dim, device=device) * -emb)# x * self.scale和emb外积emb = torch.outer(x * self.scale, emb)emb = torch.cat((emb.sin(), emb.cos()), dim=-1)return emb
  

1.7 Reference

• AIGC爆火的背后——扩散模型DDPM浅析
• 十分钟读懂Diffusion：图解Diffusion扩散模型
• 代码