奇妙数字(GESP五级202412T1)C++题解
题目传送门
B4070 [GESP202412 五级] 奇妙数字
题目描述
小杨认为一个数字 xxx 是奇妙数字当且仅当 x=pax=p^ax=pa,其中 ppp 为任意质数且 aaa 为正整数。例如,8=238=2^38=23,所以 888 是奇妙的,而 666 不是。
对于一个正整数 nnn,小杨想要构建一个包含 mmm 个奇妙数字的集合 {x1,x2,⋯,xm}\{x_1,x_2,\cdots,x_m\}{x1,x2,⋯,xm},使其满足以下条件:
- 集合中不包含相同的数字。
- x1×x2×⋯×xmx_1\times x_2\times \cdots\times x_mx1×x2×⋯×xm 是 nnn 的因子(即 x1,x2,⋯,xmx_1,x_2,\cdots,x_mx1,x2,⋯,xm 这 mmm 个数字的乘积是 nnn 的因子)。
小杨希望集合包含的奇妙数字尽可能多,请你帮他计算出满足条件的集合最多包含多少个奇妙数字。
输入格式
第一行包含一个正整数 nnn,含义如题面所示。
输出格式
输出一个正整数,代表满足条件的集合最多包含的奇妙数字个数。
输入输出样例 #1
输入 #1
128
输出 #1
3
说明/提示
样例解释
关于本样例,符合题意的一个包含 333 个奇妙数字的集合是 {2,4,8}\{2,4,8\}{2,4,8}。首先,因为 2=212=2^12=21,4=224=2^24=22,8=238=2^38=23,所以 2,4,82,4,82,4,8 均为奇妙数字。同时,2×4×8=642\times 4\times 8=642×4×8=64 是 128128128 的的因子。
由于无法找到符合题意且同时包含 444 个奇妙数字的集合,因此本样例的答案为 333。
数据范围
对于 100%100\%100% 的数据,保证 2≤n≤10122\le n\le 10^{12}2≤n≤1012。
| 子任务编号 | 得分占比 | nnn |
|---|---|---|
| 111 | 20%20\%20% | ≤10\le 10≤10 |
| 222 | 20%20\%20% | ≤1000\le 1\,000≤1000 |
| 333 | 60%60\%60% | ≤1012\le 10^{12}≤1012 |
题目大意
给定一个正整数nnn,求他的质因子个数进行某种操作后的和。
题目分析
因为x1×x2×⋯×xmx_1\times x_2\times\cdots\times x_mx1×x2×⋯×xm是nnn的因数,所以xxx中的每一项都是nnn的因数。
对于一个奇妙数字a=pba=p^ba=pb,他的所有因数都应该能写成pcp^cpc的形式且1≤b≤c1\le b\le c1≤b≤c。
因此任何奇妙数字的非111因数都是奇妙数字。
现在要构造集合xxx,我们尽可能让nnn的质因数分解式中同一个底数的指数能拆出多点的不同正整数之和。
等差数列求和
一个指数aaa(底数为ppp)要拆成尽可能小的不同正整数,那么我们先从p1p^1p1、p2p^2p2开始,如果指数之和不超过aaa,就可以继续添加元素。
那么快速求分解成多少个数的方法是什么呢?可以用等差数列求和公式。
指数aaa,枚举iii从111到无穷大,循环退出条件是i×(i+1)>ai\times(i+1)>ai×(i+1)>a,这期间最大的合法进入循环体内的iii就是以ppp为底,集合xxx中的数的数量就是iii的最大值。
举个栗子
就看样例128128128。
首先对样例进行因数分解,得272^727。
对于底数222,他的指数777中最多加出来1+2+3=61+2+3=61+2+3=6,而1+2+3+4=101+2+3+4=101+2+3+4=10超过777不合法。
1∼31\sim31∼3一共是333个数,那么222为底的集合中元素为333。
128128128没有其他的质因子,因此输出333,样例成功跟着我们的思想走了。
求指数分成多少个数的c++代码
如果穷举变量i在for外声明,可以减少一个cnt的空间。
for里面可以什么也不干,如果想劳动可以用二分
int getnum(int point) //普通版
{int i=1;for(;i*(i+1)/2<=point;i++); //for循环里啥也不用干return i-1; //i是不合法的,i-1才合法
}
int binaryGetnum(int point) //二分版
{int l=1,r=point;while(l<r){int mid=(l+r+1)/2; //防止TLEif(mid*(mid+1)/2<=point)l=mid; //合法不能+1else r=mid-1; //不合法必须-1}return l;
}
如果是普通版,时间为O(point)O(\sqrt{point})O(point);
如果是二分版,时间为O(logpoint)O(\log point)O(logpoint)。
温馨提示,log\loglog要比\sqrt{}快得多。
当然怕小伙伴们看不懂二分,我在完整代码里就用上面的函数。
没什么问题了吧?讲的很详细了吧?看代码吧!
AC完整代码
二分被注释掉了
#include<bits/stdc++.h>
using namespace std;
int getnum(int point) //普通版
{int i=1;for(;i*(i+1)/2<=point;i++); //for循环里啥也不用干return i-1; //i是不合法的,i-1才合法
}
/*
int binaryGetnum(int point) //二分版
{int l=1,r=point;while(l<r){int mid=(l+r+1)/2; //防止TLEif(mid*(mid+1)/2<=point)l=mid; //合法不能+1else r=mid-1; //不合法必须-1}return l;
}
*/
int main()
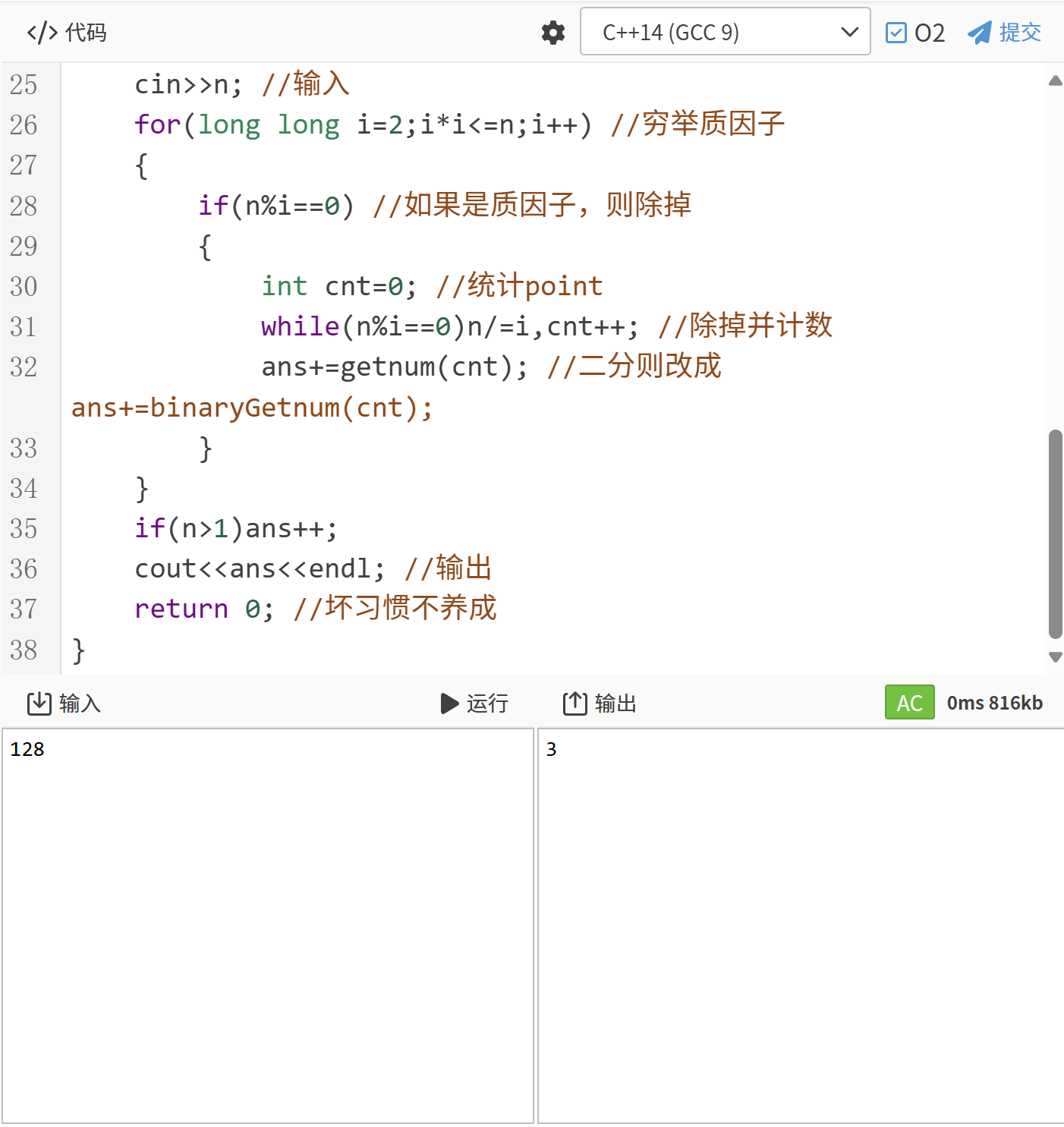
{long long n,ans=0;cin>>n; //输入for(long long i=2;i*i<=n;i++) //穷举质因子{if(n%i==0) //如果是质因子,则除掉{int cnt=0; //统计pointwhile(n%i==0)n/=i,cnt++; //除掉并计数ans+=getnum(cnt); //二分则改成ans+=binaryGetnum(cnt);}}if(n>1)ans++; //很多人不注意的地方cout<<ans<<endl; //输出return 0; //坏习惯不养成
}
当然用二分也行。
#include<bits/stdc++.h>
using namespace std;
/*
int getnum(int point) //普通版
{int i=1;for(;i*(i+1)/2<=point;i++); //for循环里啥也不用干return i-1;
}
*/
int binaryGetnum(int point) //二分版
{int l=1,r=point;while(l<r){int mid=(l+r+1)/2; //防止TLEif(mid*(mid+1)/2<=point)l=mid; //合法不能+1else r=mid-1; //不合法必须-1}return l;
}
int main()
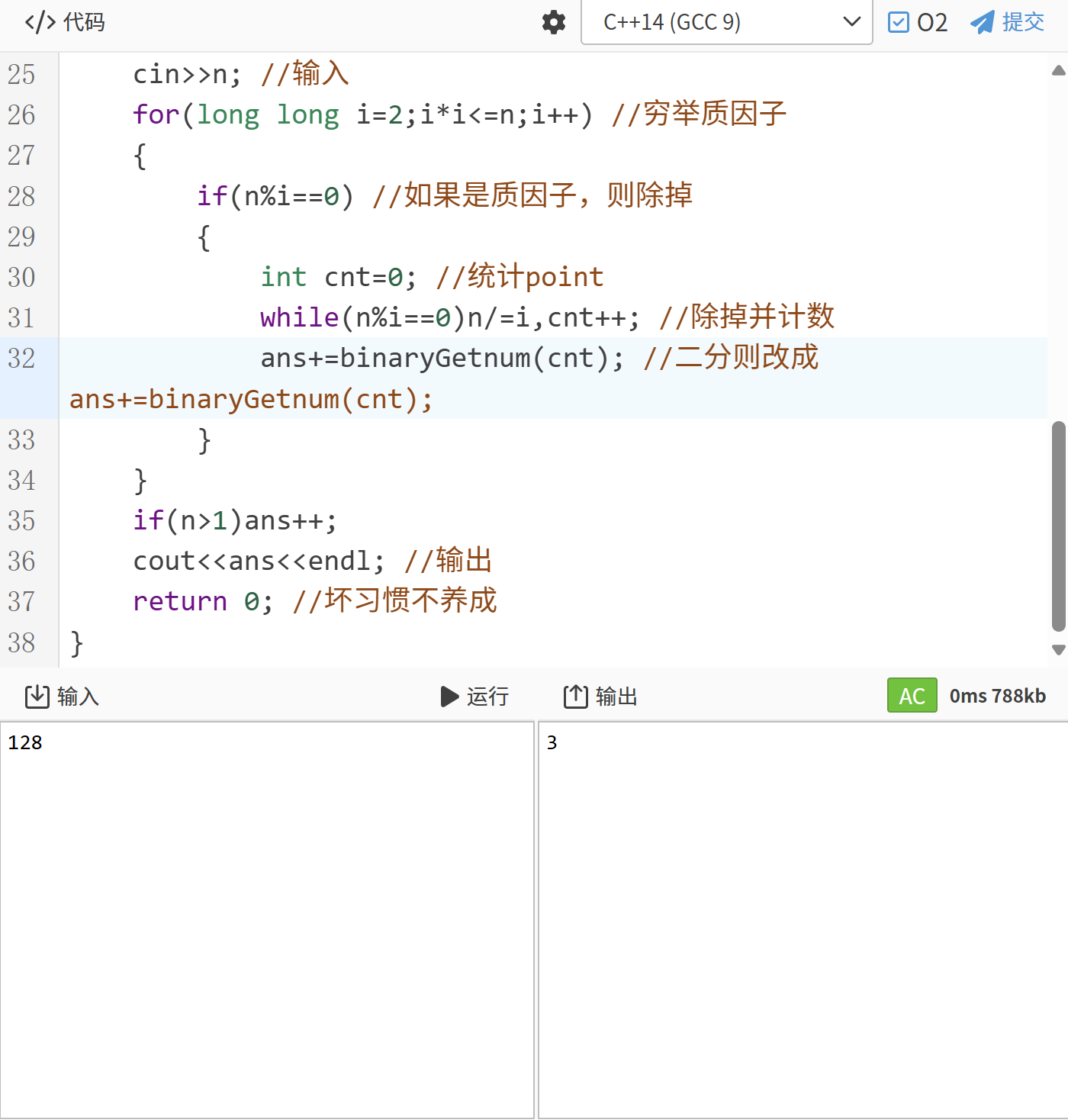
{long long n,ans=0;cin>>n; //输入for(long long i=2;i*i<=n;i++) //穷举质因子{if(n%i==0) //如果是质因子,则除掉{int cnt=0; //统计pointwhile(n%i==0)n/=i,cnt++; //除掉并计数ans+=binaryGetnum(cnt); //二分则改成ans+=binaryGetnum(cnt);}}if(n>1)ans++;cout<<ans<<endl; //输出return 0; //坏习惯不养成
}
(这是作者第一次二分一把成,点个赞吧)
复杂度分析
空间复杂度不用说了,指定O(1)O(1)O(1)。
时间复杂度
外重循环:O(n)O(\sqrt n)O(n)
内重循环1 除掉并计数:O(logn)O(\log n)O(logn)
内重循环2 getnum普通版:O(logn)O(\sqrt{\log n})O(logn)
getnum二分版:O(loglogn)O(\log\log n)O(loglogn)
可以看到内重循环2不超过内重循环1,可以不看。
总时间复杂度:O(nlogn)O(\sqrt n\log n)O(nlogn)
总结
此题不难,只要理解题意,进行简单的分析就能AC。
