吴恩达d1

无监督分类：聚类、异常检测、降维

线性回归模型：将数字拟合到一条直线上

如：单变量线性回归，只有一个特征输入

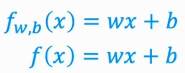输入特征x，f来预测预测值y-hat，真实值用y表示 w，b是参数

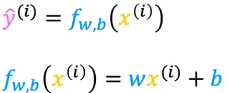i表示第几个样本

实现线性回归：

1.为了拟合，先定义成本函数，最常用平方误差成本函数，我们希望得到使成本函数最小的w，b的值。即通过J找到最优参数，J用来衡量误差。

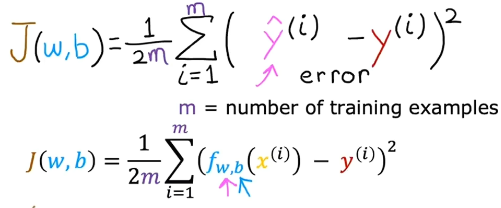
对预测与真实值的差（误差）平方求和，÷m是为了让函数值不会随着样本数增加而增加，÷2仅是为了让结果更美观没有也一样。所以J到底在做什么？

2.先简化J，令b=0，成本函数与拟合函数的关系:

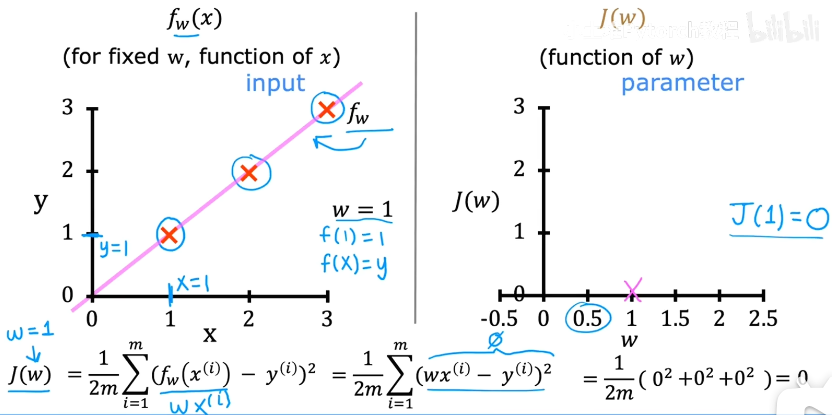
当w=1时，拟合函数f（x）=y，把3个样本点代入成本函数J，J=0

当w=0.5时，J（0.5）=0.58

当w=0时，J=2.3

最后把不同w下的J都算出来，得到完整成本函数

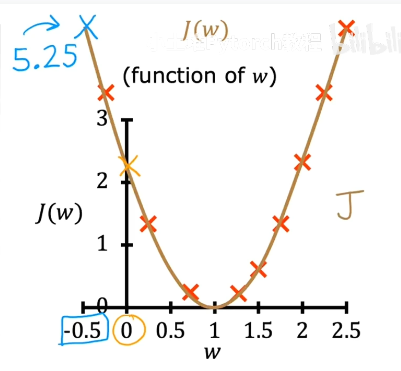由此可知w=1时J最小，即拟合最优

3.b！=0更复杂，成本函数的图像还会变成3维