当前位置：首页 > news >正文

沙姆定律原理/公式推导

news 2025/9/26 10:44:50

定律是摄影、工业视觉等领域中解决倾斜物体全平面清晰成像的核心光学原理，其核心逻辑为：当被拍摄的倾斜主体平面、镜头的等效光学平面、相机传感器所在的成像平面这三个平面调整至相交于同一条直线（沙姆线）时，原本因倾斜导致“不同区域到镜头距离不同”的主体平面，所有景物经镜头折射后均可精准汇聚到成像平面上，从而实现倾斜主体全平面无失焦的清晰成像，打破了传统对焦仅能让与镜头平行的单一焦平面清晰的局限。

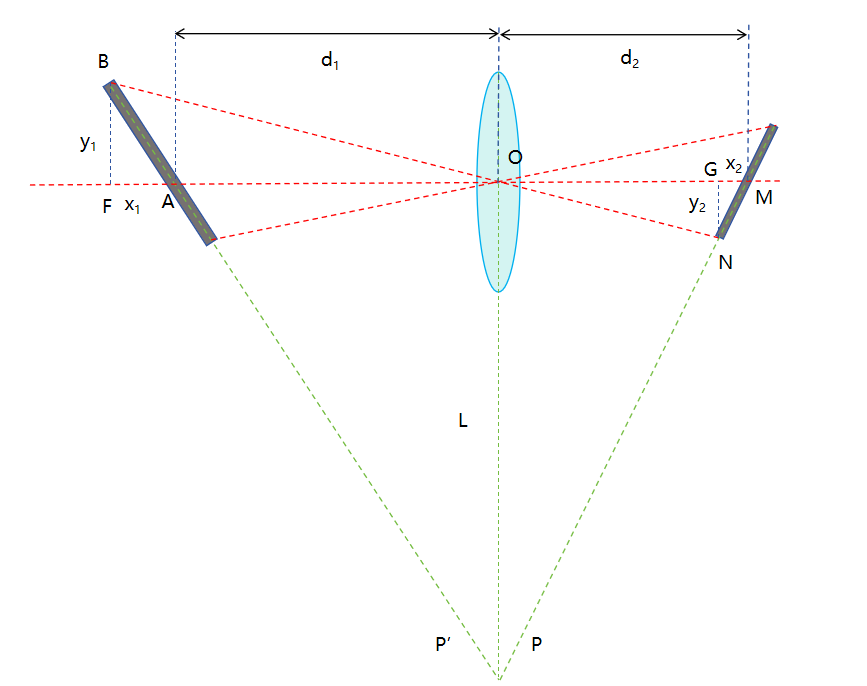
OP为镜头平面，AB为被摄主体平面在主光轴的上半部分，AB的延长线交镜头平面为P’；MN 为上半部分的成像平面，MN的延长线交镜头平面为P；A的像点为M，B的像点为N，f为焦距。图中d1=AO，d2=OM，x1=FA，x2=GM，y1=BF，y2=NG。要证明B点也能在N点清晰成像，需要证明 $1d1+x1+1d2−x2=1f\frac{1}{\mathrm{d}_1+\mathrm{x}_1}+\frac{1}{\mathrm{d}_2-\mathrm{x}_2}=\frac{1}{f}$ 如果在这个条件下P’与P 共点则说明N点可以清晰成像。
在这里插入图片描述
由物体成像公式可得：
$①:1d1+1d2=1f①:\frac{1}{d_ {1}}+\frac {1}{d_ {2}}=\frac {1}{f}$

由假设的物体成像公式可得：
$②：1d1+x1+1d2−x2=1f②：\frac {1}{d_1+x_1} +\frac {1}{d_2-x_2} =\frac {1}{f}$
由▲OBF和▲ONG 相似有：
$y1d1+x1=y2d2−x2\frac{y_1}{d_1+x_1}= \frac{y_2}{d_2-x_2}$
即：
$③：y1(d1+x1)y2=1d2−x2③：\frac{y_1}{(d_1+x_1)y_2}= \frac{1}{d_2-x_2}$
将③代入②中得：
$1d1+x1+y1(d1+x1)y2=1f\frac{1}{d_1+x_1}+ \frac{y_1}{(d_1+x_1)y_2}= \frac{1}{f}$
$1d1+x1(1+y1y2)=1f\frac{1}{d_1+x_1} \left( 1+ \frac{y_1}{y_2} \right)= \frac{1}{f}$
$d1+x1=(1+y1y2)fd_1+x_1= \left(1+ \frac{y_1}{y_2} \right) f$
可解得：
$④：x1=(1+y1y2)f−d1④：x_1= \left( 1+ \frac{y_1}{y_2} \right) f-d_1$
同样，也可解得：
$⑤：x2=d2−(1+y2y1)f⑤：x_2=d_2- \left( 1+ \frac{y_2}{y_1} \right) f$
在▲OBF和▲MNG中有:
$⑥：y1=x1⋅tan⁡a⑥：y_1=x_1 \cdot \tan a$
$⑦：y2=x2⋅tan⁡B⑦：y_2=x_2 \cdot \tan B$
由公式⑥和⑦得：
$y1y2=x1x2⋅tan⁡αtan⁡β\frac{y_1}{y_2}= \frac{x_1}{x_2} \cdot \frac{ \tan \alpha}{ \tan \beta}$
将④和⑤代入公式得：
$⑧：y1y2=(1+y1y2)f−d1d2−(1+y2y1)f⋅tan⁡αtan⁡β⑧：\frac{y_{1}}{y_{2}}= \frac{ \left( 1+ \frac{y_{1}}{y_{2}} \right) f-d_{1}}{d_{2}- \left( 1+ \frac{y_{2}}{y_{1}} \right) f} \cdot \frac{ \tan \alpha}{ \tan \beta}$
将①代入⑧得：
$y1y2=(1+y1y2)d1d2d1+d2−d1d2−(1+y2y1)d1d2d1+d2⋅tan⁡αtan⁡β\frac{y_1}{y_2}= \frac{ \left( 1+ \frac{y_1}{y_2} \right) \frac{d_1d_2}{d_1+d_2}-d_1}{d_2- \left( 1+ \frac{y_2}{y_1} \right) \frac{d_1d_2}{d_1+d_2}} \cdot \frac{ \tan \alpha}{ \tan \beta}$

$\frac{\frac{-d^2}{d_1+ d_2}+\frac{d_1d_2}{ d_1+d_2}\times\frac{y_1}{ y_2}}{\frac{{d_2}^2}{d_1+d_2}-\frac{{d}_1d_2}{{d}_1+d_2}\times\frac{y_2}{y_1}}\cdot\frac{\tan\alpha}{\tan\beta}=\frac{{d}_1\left(\frac{y_1}{y_2}d _2-{d}_1\right)}{d_2\left( d_2-\frac{y_2}{y_1} {d}_1\right)}\cdot\frac{\tan\alpha}{\tan\beta}$

$=d1d2⋅y1y2⋅tan⁡αtan⁡β=\frac{d_1}{d_2} \cdot \frac{y_1}{y_2} \cdot \frac{ \tan \alpha}{ \tan \beta}$
即：
$y1y2=d1d2⋅y1y2⋅tan⁡αtan⁡β\frac{y_1}{y_2}= \frac{d_1}{d_2} \cdot \frac{y_1}{y_2} \cdot \frac{ \tan \alpha}{ \tan \beta}$
最终得：
$d1⋅tan⁡a=d2⋅tan⁡βd_{1} \cdot \tan a=d_{2} \cdot \tan \beta$
所以，在被拍摄的倾斜主体平面、镜头的等效光学平面、相机传感器所在的成像平面这三个平面调整至相交于同一条直线时，物体可以在传感器上清晰成像。