当前位置：首页 > news >正文

Qt容器QList、QLinkedList、QVector特性浅谈

news 2025/9/26 10:41:48

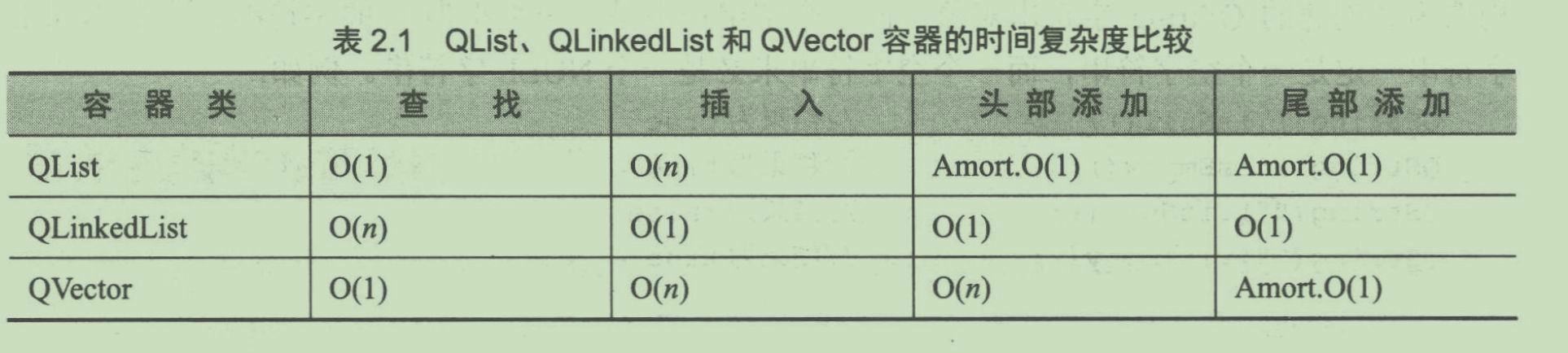
要理解这张表，需结合时间复杂度的概念和 Qt 容器的特性，分“表格结构”“时间复杂度基础”“各容器操作解析”“容器选择逻辑”四部分拆解：

表头是4种操作：查找、插入、头部添加、尾部添加；

行是3个 Qt 容器类：QList、QLinkedList、QVector；

单元格内容是该操作在对应容器下的时间复杂度（衡量算法效率的核心指标，反映操作耗时随数据规模增长的趋势）。

时间复杂度用「大O符号」（如 O(1)、O(n)）描述算法执行时间随数据规模 n（容器元素个数）增长的变化趋势：

O(1)：常数时间。操作耗时与 n无关，无论数据多少，耗时基本固定（如数组“随机访问”）。
O(n)：线性时间。操作耗时与 n成正比，数据越多，耗时越长（如链表“遍历查找”）。
Amort.O(1)：均摊常数时间。单次操作可能偶尔耗时 O(n)（如数组扩容时复制元素），但多次操作的平均耗时仍为 O(1)（动态数组的典型特性）。

QList 基于动态数组+链表节点预留实现，核心优势是“随机访问快 + 头部/尾部操作高效”。

操作	时间复杂度	解析
查找	O(1)	支持索引直接访问（类似数组），无需遍历，耗时与数据量 n无关。
插入	O(n)	非尾部插入需移动后续所有元素（如第 k位插入，后 n−k个元素后移），耗时随 n线性增长。
头部添加	Amort.O(1)	理论上需移动所有元素（O(n)），但内部预留空间，多数情况无需全移；少数扩容场景耗时 O(n)，但多次操作平均后为常数时间。
尾部添加	Amort.O(1)	同动态数组逻辑：预留空间则直接插入（O(1)），空间不足时扩容（O(n)），长期平均为常数时间。

QLinkedList 是双向链表，核心优势是“插入/删除本身高效（指针操作），头部/尾部操作极快”，但随机访问极慢（需遍历）。

操作	时间复杂度	解析
查找	O(n)	链表无随机访问能力，需从头部/尾部逐个遍历节点，耗时与 n成正比。
插入	O(1)	链表“插入动作本身”（修改前后节点的指针）是常数时间，但前提是已定位到插入位置（若包含“定位”，总时间为 O(n)；表格默认指“定位后仅执行插入”的耗时）。
头部添加	O(1)	新建节点，修改其 `next`（指向原头节点）和原头节点的 `prev`（指向新节点），再更新头指针，仅需指针操作，耗时与 n无关。
尾部添加	O(1)	双向链表尾部逻辑同头部：新建节点，修改 `prev`（原尾节点）和 `next`（新节点），更新尾指针，指针操作耗时固定。

QVector 基于连续动态数组实现，核心优势是“随机访问极快 + 尾部操作高效”，但头部/中间插入极慢（需移动元素）。

操作	时间复杂度	解析
查找	O(1)	索引直接访问内存元素（数组特性），耗时与 n无关。
插入	O(n)	非尾部插入需移动后续所有元素（如第 k位插入，后 n−k个元素后移），耗时随 n线性增长。
头部添加	O(n)	连续存储特性导致：头部添加需将所有 n个元素后移一位，耗时与 n成正比。
尾部添加	Amort.O(1)	同动态数组逻辑：预留空间则直接插入（O(1)），空间不足时扩容（O(n)），多次操作平均后为常数时间。

表格的本质是为“操作场景”匹配最优容器，核心思路是：

核心需求	推荐容器	原因
频繁随机访问 + 少量头尾操作	QList / QVector	两者查找均为 O(1)；QList 对非尾部插入更友好，QVector 内存更紧凑。
频繁任意位置插入/删除	QLinkedList	插入/删除本身是 O(1)（仅需改指针），但需先“定位”（若定位耗时高则需权衡）。
极致头尾操作 + 随机访问	QList	头尾添加均摊 O(1)，查找 O(1)，平衡头尾与随机访问需求。
内存紧凑 + 大规模数据 + 随机访问	QVector	连续存储对 CPU 缓存友好，适合性能敏感的大数据场景。