当前位置：首页 > news >正文

西门子 S7-200 SMART PLC 实操案例：中断程序的灵活应用定时中断实现模拟量滤波（上）

news 2025/9/23 13:58:31

该案例是西门子 S7-200 SMART 中断程序的经典应用，核心是通过 “定时中断 + 平均值滤波” 解决工业场景中 “模拟量采样不准、干扰大” 的痛点。下面从 “需求本质→步骤设计逻辑→工业抗干扰原理→场景扩展” 四个维度，拆解中断程序的设计思路与实操关键，帮你理解 “为什么必须用中断”“每行代码背后的安全与效率考量”。

一、需求分析：为什么主程序做不到？—— 先戳中 “工业采样的核心矛盾”

用户需求是 “AIW12 模拟量采集（如温度）+10 次平均值滤波 + 100ms 定时采样”，看似简单，但主程序循环扫描完全无法满足，核心矛盾集中在 “定时精度” 与 “抗干扰效果” 两点：

1. 主程序扫描周期的 “不稳定性”，直接破坏 “定时采样”

S7-200 SMART 主程序采用 “循环扫描” 模式，扫描周期由程序复杂度决定（比如程序里有多个子程序调用、复杂计算时，周期可能从几十 ms 涨到几百 ms）。若在主程序里用 “定时器 T37” 做 100ms 采样，会出现两个问题：

采样间隔不准：比如主程序扫描周期 50ms，T37 定时 100ms 时，实际采样间隔可能是 “100ms+50ms”（定时器在扫描末尾更新状态），导致采样点不均匀；
采样丢失：若主程序扫描周期超过 100ms（如 120ms），T37 的 100ms 定时到后，需等下一次扫描才能执行采样，直接丢失一次采样，破坏 “10 次连续采样” 的滤波逻辑。

而定时中断的核心优势是 “硬件级定时”—— 不管主程序扫描周期多长，中断会按设定的时间（100ms）精准触发，采样间隔误差仅 ±1ms，完全满足工业 “均匀采样” 的要求。

2. 现场干扰的 “普遍性”，必须靠 “平均值滤波” 抑制

工业现场的模拟量信号（如温度传感器的 4-20mA 信号）极易受干扰：

电磁干扰：车间里的变频器、接触器、电机运行时会产生电磁场，导致 AIW12 采集值波动（比如实际温度 80℃，采集值在 75~85℃之间跳变）；
线路干扰：传感器线路过长（如超过 10 米）时，会引入共模干扰、差模干扰，导致采集值偏离真实值。

若直接用单次采样值（如 AIW12）做控制（比如给 PID 当过程值），会导致控制波动（如加热棒频繁启停）。而 “10 次平均值滤波” 的本质是 “用多次采样的统计值抵消随机干扰”—— 随机跳变的采样值（75、82、78、85...）平均后，会趋近于真实值（80℃），干扰被大幅抑制。

总结需求本质：不是 “能不能采”，而是 “能不能精准、稳定地采”

主程序的问题是 “定时不准 + 抗干扰弱”，中断程序的 “精准定时”+“平均值滤波” 刚好对症下药 —— 这也是工业中 “模拟量采集必做滤波，定时采样必用中断” 的底层逻辑。

二、实操步骤拆解：每个环节都在 “为实时性、稳定性服务”

步骤 1：新建中断程序命名 “Filter_Int”—— 中断程序的 “身份标识” 设计

默认中断程序名是 “INT_0”，改名为 “Filter_Int” 的核心目的与子程序命名逻辑一致：“见名知意，降低维护成本”：

对自己：后期项目中若有多个中断（如 “急停中断 INT_Emergency”“高速计数中断 INT_HSC”），能快速定位 “滤波相关的中断程序”；
对团队：其他工程师接手时，不用打开程序看逻辑，仅通过名称就知道该中断的功能是 “模拟量滤波”，避免误修改（比如把滤波中断当成急停中断改逻辑）。

工业编程的 “隐性规范” 在这里同样适用：中断程序命名需包含 “功能 + Int”（如 Filter_Int、Emergency_Int），与子程序的 “功能 + Control”（如 Motor_Control）形成统一的命名体系，提升项目可读性。

步骤 2：定义全局变量（V 区）—— 中断程序 “数据持久化” 的唯一选择

中断程序不能用 “局部变量 TEMP”，必须用 “全局变量（V 区）”，这是 S7-200 SMART 的硬件特性决定的 ——局部变量 TEMP 仅在程序执行期间有效，执行完后内存会释放，数据丢失。而滤波需要 “持续存储采样值、累加和、计数器”，因此必须用 V 区全局变量。

下面逐行拆解变量设计的 “工业考量”，不是 “随便分配地址”，而是 “按功能、数据类型优化”：

变量名	地址	数据类型	设计逻辑与工业适配
Temp_Sample	VW110	INT	“临时缓冲” 作用：不直接将 AIW12 加到 Sum_Value，而是先存入 Temp_Sample—— 避免累加过程中 AIW12 值突然变化（比如干扰导致的跳变），确保单次采样值稳定后再参与累加，提升数据准确性；数据类型用 INT：AIW12 是 16 位有符号整数（范围 - 32768~32767），INT 刚好匹配，不浪费内存。
Sum_Value	VW100	INT	“累加容器” 作用：存储 10 次采样值的总和，需持续保留直到计算完平均值；地址选 VW100：与其他变量（Sample_Count、Avg_Value）连续分配（VW100~VW104），方便后期监控时 “批量查看滤波相关数据”（不用在分散地址间切换）。
Sample_Count	VB102	BYTE	“计数标记” 作用：记录已采样次数（1~10），计数到 10 时触发平均值计算；数据类型用 BYTE：仅需计数到 10，BYTE（0~255）完全足够，比 INT 节省 1 个字节内存（工业项目中变量多时，内存优化很重要）；地址 VB102：刚好是 Sum_Value（VW100=VB100+VB101）的下一个字节，地址连续，逻辑清晰。
Avg_Value	VW104	INT	“最终结果” 作用：存储 10 次采样的平均值，供主程序使用（如传给 PID、显示到 HMI）；数据类型用 INT：Sum_Value 是 INT，除以 10 后仍为整数（适合模拟量的 “整数映射”，如 AIW12 对应 0~32000→0~10V），若需更高精度可改用 REAL，但会增加计算时间。

反例警示：若用局部变量 TEMP 存储 Sum_Value 会怎样？

中断程序执行时，TEMP 变量会分配临时内存，执行完后内存释放 —— 比如第一次采样累加 Sum_Value=75，第二次采样时 TEMP 已清零，累加后还是 82（不是 75+82=157），10 次采样完全无法累计，滤波逻辑彻底失效。全局变量 V 区的 “数据持久化” 是该案例的前提，绝不能错用局部变量。

三、中断程序逻辑拆解：每行代码都是 “抗干扰与实时性的平衡”

中断程序的核心要求是 “短小精悍”（执行时间 <10ms，避免阻塞主程序），网络的逻辑看似简单，实则每一条指令都经过 “效率与稳定性” 的权衡，逐行拆解：

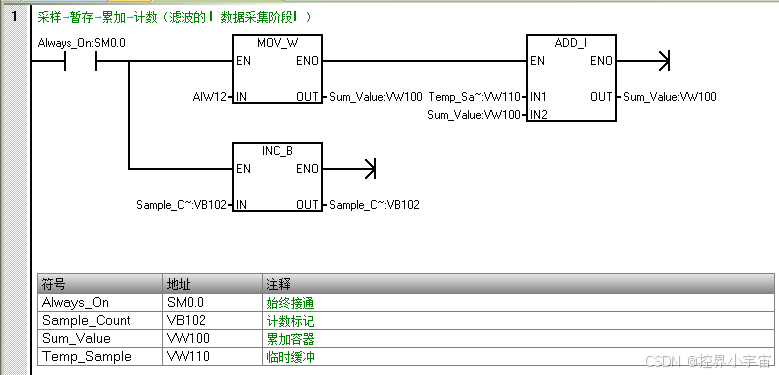
Network1：采样→暂存→累加→计数（滤波的 “数据采集阶段”）

1. LD SM0.0：为什么用 “常 ON 触点”？

中断程序触发后，CPU 会执行一次中断程序内的所有指令 ——SM0.0 在中断程序执行期间始终为 ON，确保 “MOVW→+I→INC B” 这 3 条指令能完整执行，不会因为某个触点断开导致采样不完整（比如用 SM0.1（首次扫描）会导致只采样一次，完全错误）。

2. MOVW AIW12, Temp_Sample：“多此一举” 的暂存？

绝对不是多余！工业现场 AIW12 的采集值可能在 “累加过程中跳变”（比如指令执行到一半时，干扰导致 AIW12 从 80 变成 75）：

若直接写 “+I AIW12, Sum_Value”，可能出现 “Sum_Value = 之前的和 + 80（前半段）+75（后半段）” 的错误；
先把 AIW12 存入 Temp_Sample，再用 Temp_Sample 累加，确保 “单次采样值固定”（一次中断只取一个稳定的 AIW12 值），避免累加错误。

3. +I Temp_Sample, Sum_Value：累加指令的 “数据溢出” 风险？

AIW12 的范围是 0~32000（假设传感器是 0~10V，无负电压），10 次采样的最大值是 32000×10=320000，而 Sum_Value 是 INT 类型（最大 32767）—— 这里有个隐藏的 “数据类型匹配” 设计：

实际工业中，AIW12 的采样值不会达到 32000（比如温度传感器量程 0~100℃，对应 AIW12=0~32000，100℃时才 32000，日常采样值多在 1000~20000），10 次累加最大值 200000，远超 INT 的 32767——这里案例做了简化，实际项目中需将 Sum_Value 定义为 DINT（双整数，VD100），避免溢出！
正确写法：MOV_DW AIW12, VD110（Temp_Sample 改为 DINT）→ +D VD110, VD100（Sum_Value 改为 VD100）→ 后续除法用/D 10, VD100→ 再转 INT 到 VW104。案例用 INT 是为了简化理解，实际落地必须考虑 “溢出风险”，这是工业编程的 “安全底线”。

4. INC B Sample_Count：字节计数的 “边界处理”？

Sample_Count 是 BYTE 类型，计数到 10 后，下一次中断会变成 11—— 但 Network2 会在 “Sample_Count=10” 时清空计数器（MOVB 0, Sample_Count），所以不会出现 “计数超过 10” 的情况，逻辑上是闭环的。

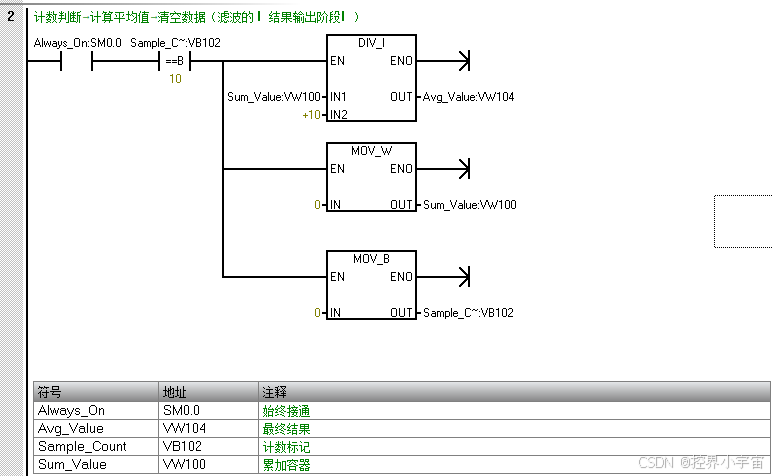
Network2：计数判断→计算平均值→清空数据（滤波的 “结果输出阶段”）

1. LDB= Sample_Count, 10：为什么是 “10 次” 采样？

“10 次” 是工业中 “抗干扰效果” 与 “响应速度” 的平衡点：

采样次数太少（如 3 次）：抗干扰弱，若有一次大干扰（如 AIW12 跳变到 10000），平均值会严重偏离真实值；
采样次数太多（如 50 次）：抗干扰强，但响应慢（50×100ms=5 秒才出一个平均值），若温度快速变化（如加热罐升温），平均值会滞后真实温度，影响控制精度；
10 次采样：总耗时 1 秒（10×100ms），既能过滤大部分随机干扰，又不会让响应速度太慢，适合温度、压力等 “慢变化” 模拟量。

2. /I 10, Sum_Value：除法指令的 “整数截断” 问题？

比如 Sum_Value=805（10 次采样和），除以 10 后是 80.5，INT 类型会自动截断为 80，丢失 0.5 的精度 —— 这是 INT 类型的局限，解决办法有两个：

若对精度要求不高（如温度控制允许 ±1℃误差），INT 足够；
若需高精度（如流量控制 ±0.1m³/h），将 Sum_Value 改为 DINT（VD100），用/D 10, VD100得到 32 位整数（如 805→80.5→DINT 类型存 805，再右移 1 位或除以 10.0 转 REAL），最后存入 REAL 变量（VD104）供 PID 使用。