当前位置： 首页 > news >正文

【 C/C++ 算法】入门动态规划-----路径问题（以练代学式）

news 2025/9/23 12:14:19

在这里插入图片描述>每日激励：“不设限和自我肯定的心态：I can do all things。 — Stephen Curry”

绪论​：
本章是动态规划的第二篇，本章将开始二维的动态规划，在二维中的动态规划本质和一维的分析来说差不太多，只不过状态表示从一维变成了二维，而在二维上所能管理的状态就从一维的两个变成了二维的三个，也就是x轴，y轴，数组中的值。若没看了解过动规算法，我强烈建议先看第一篇blog，因为当你看完第一篇你就对动规基本认识了，其中也就能认识到它的五步骤分析法，这里也就不扩充说明而是直接使用了
————————
早关注不迷路，话不多说安全带系好，发车啦（建议电脑观看）。

路径问题🛣️

本章主要还是在二维数组中的进行的动态规划：
同样还是五步走：状态表示、状态方程、初始化、移动方向、返回结果

  1. 其中在二维中状态表示就会和一位略有不同，不同本质一样：
    从以 i 结尾.，… ==》 从左上角到达 i j 位置，…
    1. 当然在最后一题中发现上面这种常规方法实现不通，因为状态方程会受后面状态影响
    2. 所以换种思路：以 i j 位置开头到结尾，…
  2. 状态方程和初始化则要考虑到题目，在二维数组中进行推算状态方程和需要初始的值
    1. 初始化中一定要分析清楚开始的状态，保证开始的状态中获取的值不错且保证后续正常进行
    2. 状态方程则是在状态表示之后根据题目来进行分析，一般来说通过使用前面的状态来计算（当前状态会收到前后影响而出不来结果时就需要考虑状态表示是否正确）

光说较为抽象，建议看完下述五道题后再回顾上述总结🍔🍔

5. 不同路径🙃

题目🗒️：

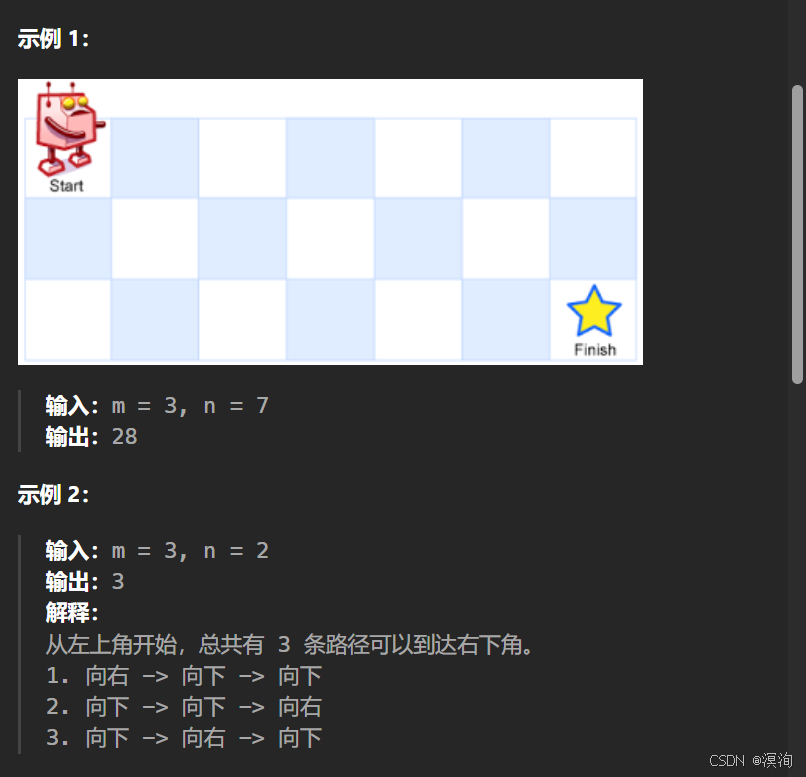
在这里插入图片描述
在这里插入图片描述

分析题目并提出，解决方法🎈：

在 3 * 2 的网格中的走法：
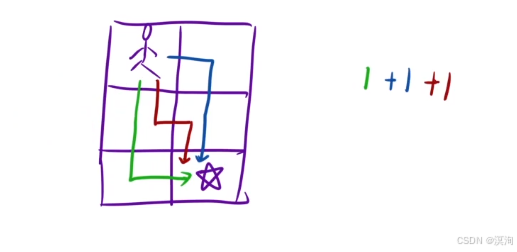
在这里插入图片描述

  1. 状态表示：dp[i][j]，走到[ i ][ j ]位置的时候，一共有多少中方式
    1. 经验 + 题目要去
    2. 以 [i,j] 为结尾，题目要求
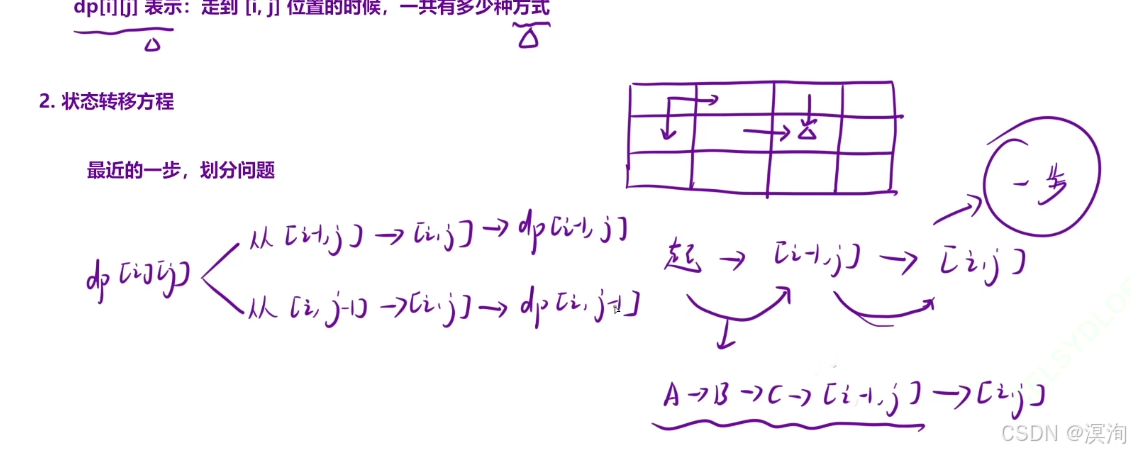
  2. 状态转移方程
    1. 最近一步，划分问题：
    2. 注意的是，此处求的是到达[ i, j ] 位置的方法，而不是步数
    3. 所以直接等于（ dp [ i - 1，j ] + dp [ i ，j - 1 ]）都不需要+1
      在这里插入图片描述
  3. 初始化
    1. 目的：填表的时候不越界，并且根据题意填写
    2. 对于二维的来说：通常多加一行和一列的方式来进行防止越界
    3. 注意下标映射和虚拟节点里面的值是正确的
    4. 让边缘格子的初始化方法为1（对于第一个位置来说，他肯定能有一种方法到达，而转移方程是从左和上获取值，那么选择其中一个位置填充1即可），这里将 dp[ 0 ][ 1 ] 位置为 1 即可，这样边缘的位置通过状态转移方程都能变成1：
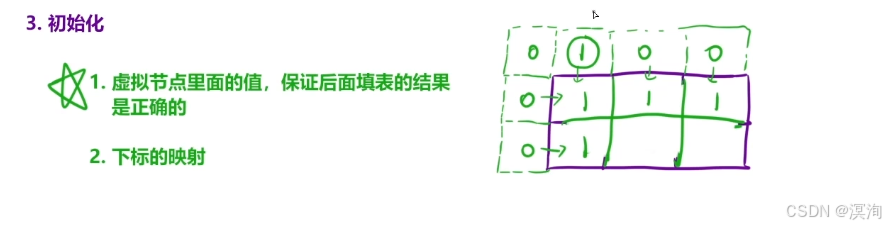
      在这里插入图片描述
  4. 填表顺序：从上往下填写每一行，每一行从左往右
  5. 返回值dp[m][n]

题解核心逻辑⭐：

class Solution {
public:int uniquePaths(int n, int m) {vector<vector<int>> dp(n+1,vector<int>(m + 1));dp[0][1] = 1;for(int i = 1 ; i <= n ;i++){for(int j = 1; j <= m;j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[n][m];}
};

6. 不同路径 II🛣️🛣️

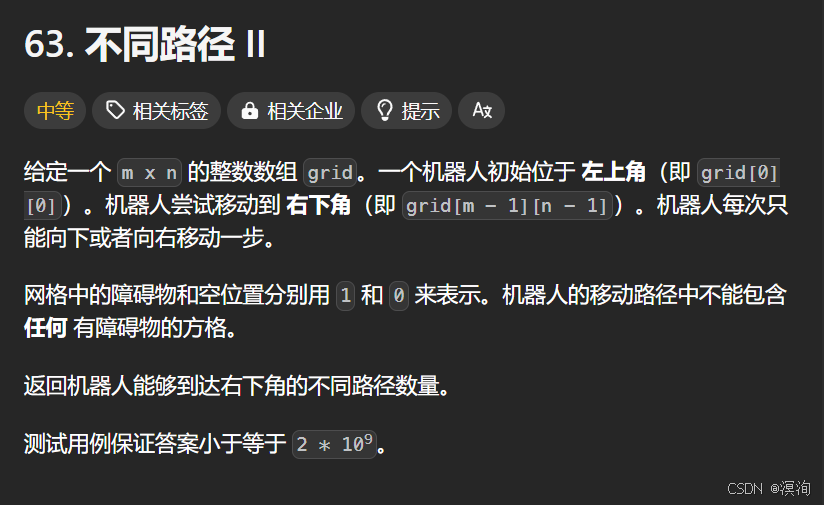
题目🗒️：

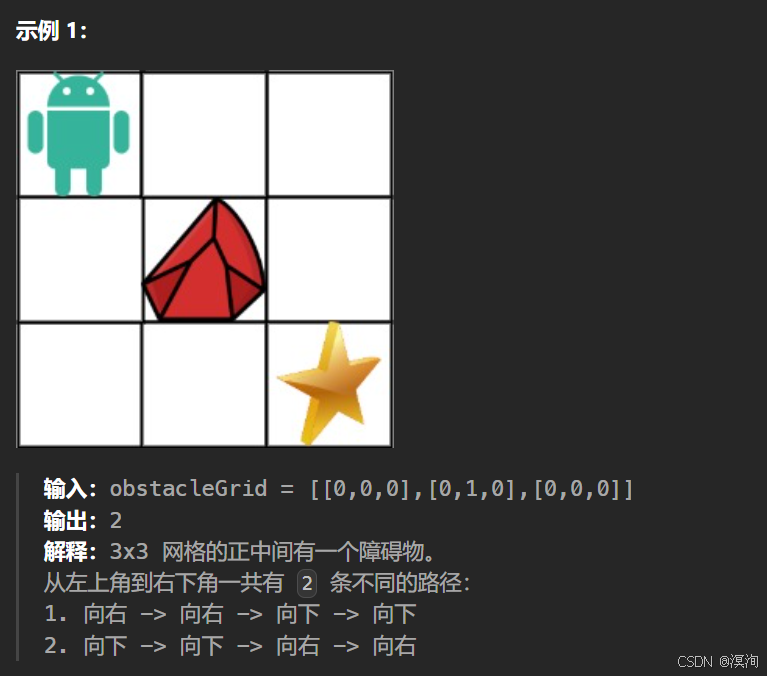
在这里插入图片描述

在这里插入图片描述

题解核心逻辑😗：

本题和上题一样，只不过加了一个障碍物，而对于这个障碍物的话，当我们遇到这一点时不进入即可，这样它的dp[i][j] = 0，也代表0种方法，也就不影响下面的转移方程，本质也就是一个判断

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {//使用动态规划：因为可以将结果存放到一个容器中，并且结果也能通过这个容器来获取//dp[i][j]：到达i j位置是，不同路径的数量//dp[i][j] = dp[i-1][j] + dp[i][j-1] ：当前 i j 位置到达的个数，等于左边 上边的和//其中注意的是，若左或上为obstacle则不进行计算，填为0即可int n = obstacleGrid.size(),m = obstacleGrid[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1,0));dp[0][1] = 1;//默认填充一个方法，可以理解为 1 1 大小时for(int i = 1; i <= n;i++){for(int j = 1; j <= m;j++){if(obstacleGrid[i-1][j-1] == 1) continue;dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[n][m];}
};

7. 珠宝的最高价值💸

题目🗒️：

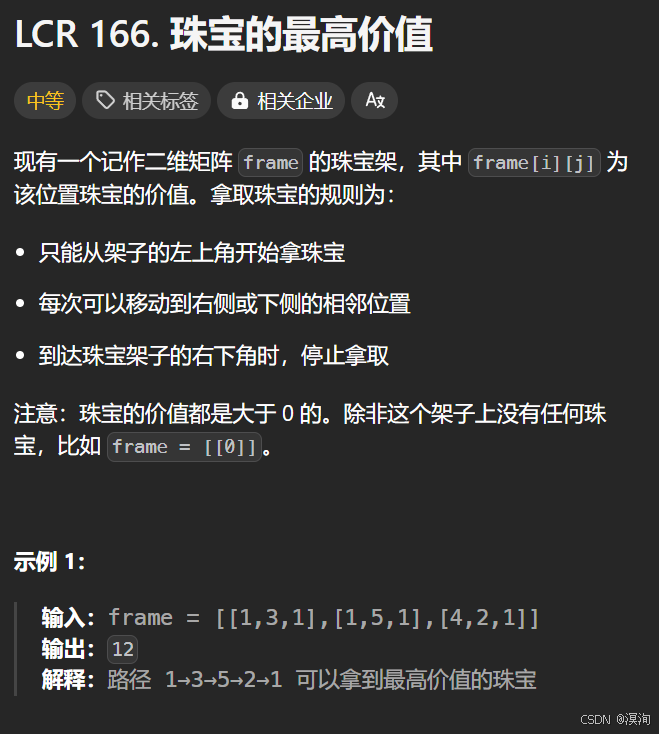
在这里插入图片描述

分析题目并提出，解决方法🎈：

  1. 状态表示：dp[ i ][ j ]：到达[ i , j ]位置的时候，此时的最大价值
    1. 经验 + 题目要求
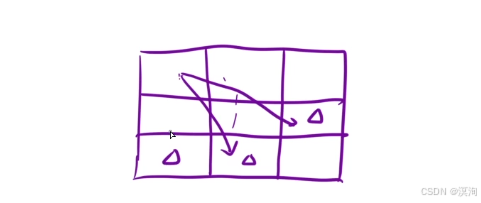
      在这里插入图片描述
  2. 状态转移方程
    1. 最近的状态，也就是从上面，要么从左边走过来
    2. 并且要的是最大值，所以取最大值
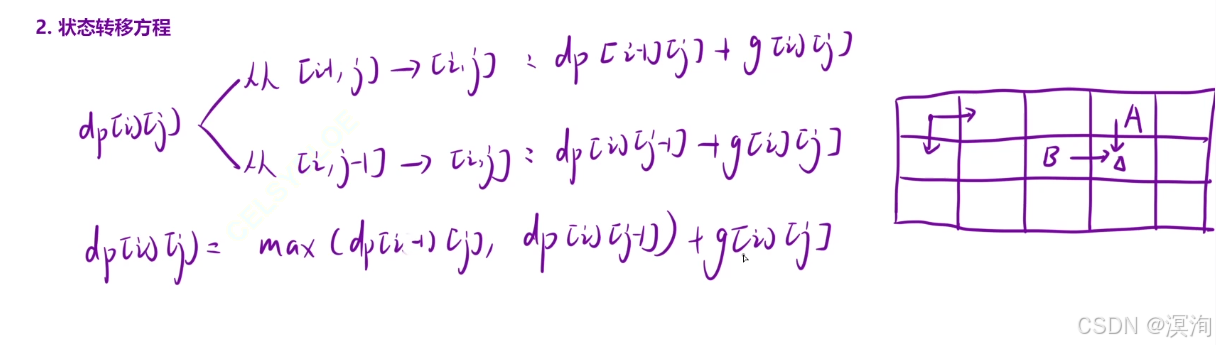
      在这里插入图片描述
  3. 初始化
    1. 里面的值，要保证后面填表是正确的：本题填0即可，因为对于边缘从上或者左边位置到达自身都是可以不用看的（最大价值为0）
    2. 下标的映射（多加了一个行，对于取值的矩形来说 n-1 m-1）
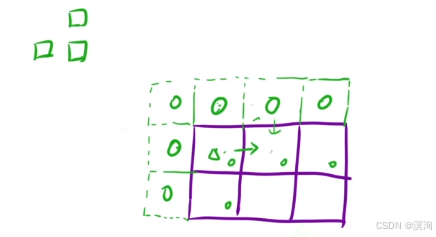
      在这里插入图片描述
  4. 填表顺序：从上到下，从左到右

题解核心逻辑：

此处就不用初始化了，因为多加的行列价值为0
这里总结下，对于分析初始化：

  1. 第一个方向：通过状态表示进行分析，通过状态表示确定要初始化地方的值（但这个有点局限）
  2. 第二个方向：主要是通过第一个位置来分析，分析第一个位置需要那些值来进行初始化，并根据题目确定第一个位置的值最终为多少，为多少就取决于状态方程和初始化的值得到 ！！

那本题分析：第一个位置是 1 1，进行计算时的状态方程为max(dp[i - 1][j],dp[i][j-1]) + frame[i-1][j-1]。那么就要考虑：dp[i - 1][j]和dp[i][j-1]，而分析题意可以知道第一个位置肯定是不用加上之前的价值的，所以这两个地方填0即可，或者说直接不动使用默认的0即可

class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {//思想和上一题以及第一题基本一样，只不过，状态表示以及转移方程不一样   //dp[i][j]；到达 i j 位置时，能获取的最大价值//dp[i][j] = max(dp[i - 1][j],dp[i][j-1]) + frame[i-1][j-1] //其中的frame[i-1][j-1]本质就是frame[i][j]，这不过在循环中因为dp多加一行一列int n = frame.size(),m = frame[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1,0));for(int i = 1; i <= n;i++){for(int j = 1; j <= m;j++){dp[i][j] = max(dp[i - 1][j],dp[i][j-1]) + frame[i-1][j-1];}}return dp[n][m];}
};

8. 下降路径最小和🦈

题目🗒️：

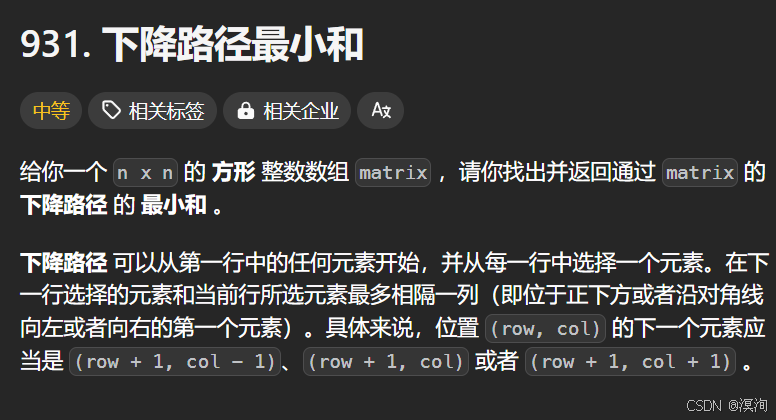
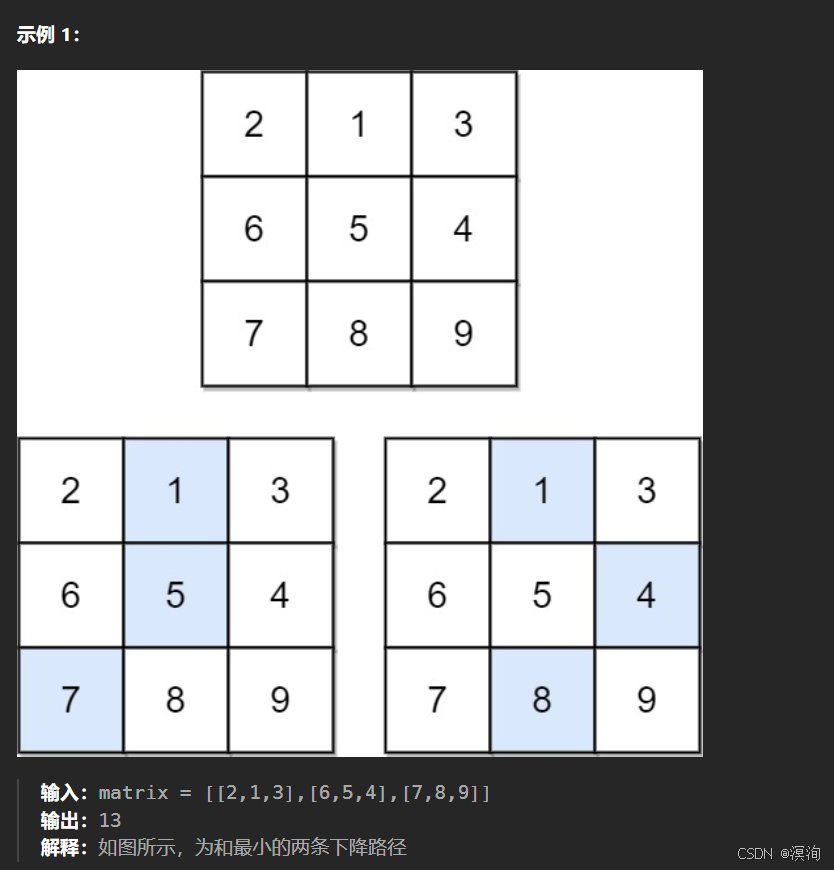
在这里插入图片描述
在这里插入图片描述

分析题目并提出，解决方法🤔：

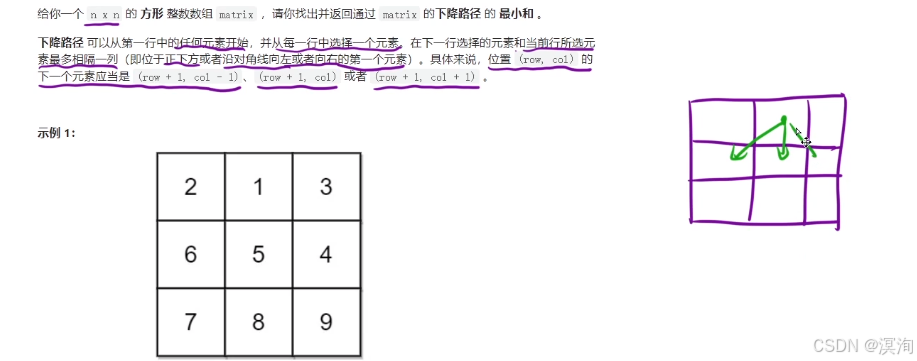
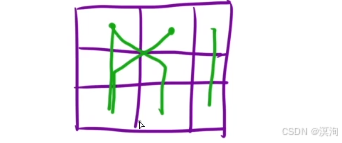
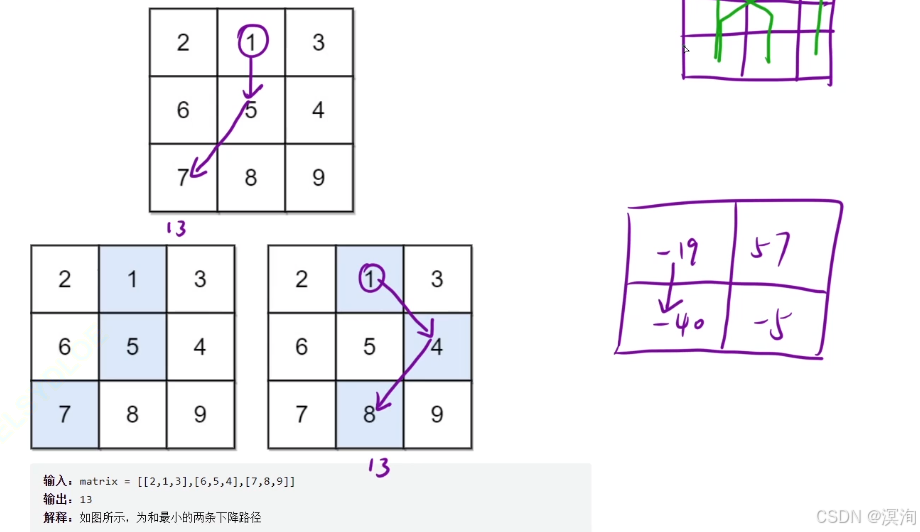
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

题解核心逻辑🚑：

  1. 状态表示：dp[ i ][ j ]：到达 [ i , j ] 位置时，最小的下降路径
    1. 经验 + 题目要求：
  2. 状态转移方程：
    1. 从三个方向的最小下降路径 + 当前位置的值
      在这里插入图片描述
  3. 初始化：
    1. 此处需要注意的是越界问题
    2. 因为要用到左边和右边以及上面三个方向的值所以就需要防止越界，那么最右和左上角的看，就需要多增一行两列
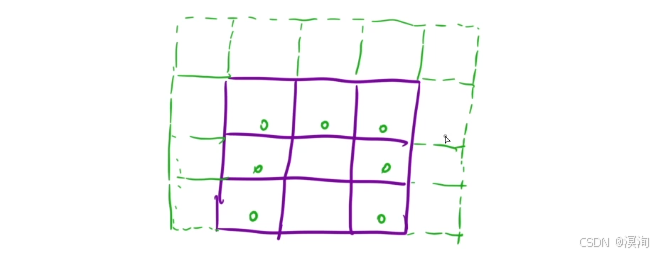
      在这里插入图片描述
    3. 需要再注意的是：保证里面的值是正确的，以及下标的映射
    4. 其中对于左右两列不能初始化为0，因为本题要求的是最小值，如果直接填0，就很有可能会取到，所以应该填正无穷大（直接全部先全部正无穷大，然后再初始化第一行为0，或者直接全部初始化为最大值，在代码内部进行特殊处理）
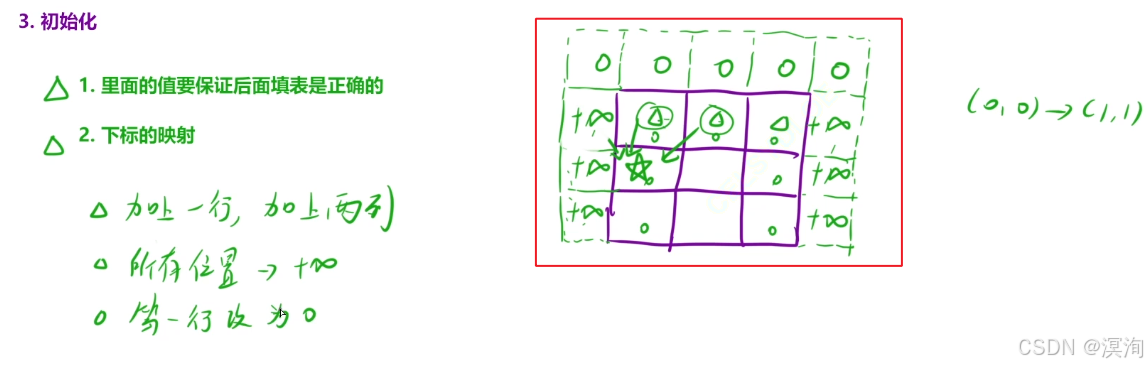
      在这里插入图片描述
  4. 填表顺序：整体：从上往下（同一行顺序随便是不影响的）
  5. 返回值：最后一行的最小值

源码

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {//1. dp表int n = matrix.size();vector<vector<int>> dp(n+1,vector<int>(n+2,INT_MAX));//注意本题需要多开 1行 2列，并且全部先初始化为无穷大for(int i = 0; i < n + 2;i++) dp[0][i] = 0;//再将第一行初始化为0for(int i = 1;i <= n;i++){for(int j = 1; j <= n;j++){int m = min(dp[i-1][j-1],dp[i-1][j]);dp[i][j] = min(m,dp[i-1][j+1]) + matrix[i-1][j-1];//取处三个方向的最小值 + 当前位置的值}}int retmin = INT_MAX;for(int i = 1;i <= n;i++){retmin = min(retmin,dp[n][i]);}return retmin;}
};//解法二：基本思想保持一致，只不过初始化方法不同导致内部判断会不同一点
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {//dp[i][j]：到达 i j 时，下降路径的最小和//dp[i][j] = min(dp[i-1][0],dp[i-1][1],...,dp[i-1][m-1]) + matrix[i-1][j-1]//同样的多开一行两列//其中初始化就要注意了，因为min函数取较小值的原因所以不能初始化为0，那么就可以初始化为最大值int n = matrix.size(),m = matrix[0].size();vector<vector<int>> dp(n+1,vector<int>(m+2,INT_MAX));//多开一行两列for(int i = 1; i <= n;i++){for(int j = 1; j <= m;j++){int minval = min(min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1]);if(minval == INT_MAX) minval = 0; //单独处理下第一行dp[i][j] = minval + matrix[i-1][j-1];}}int ret = dp[n][0];for(int index = 0; index <= m;index++) ret = min(ret,dp[n][index]);return ret;}
};

9. 最小路径和😗

题目🎈：

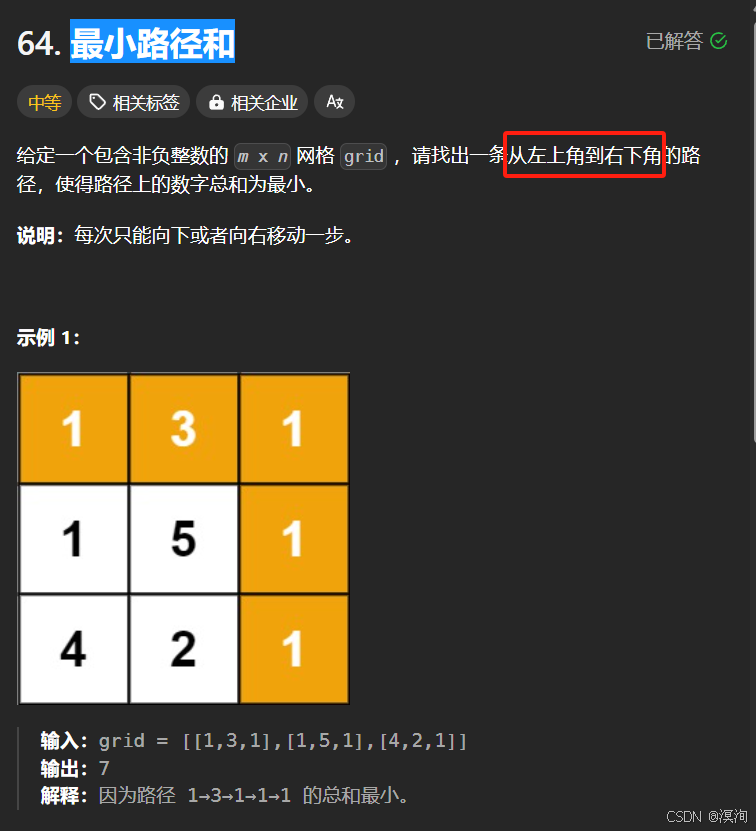
在这里插入图片描述

题解核心逻辑🛴：

  1. 通过分析得出：
  2. 状态表示：dp[i][j]表示以 i j 位置结尾，路径上总和的最小值
  3. 状态转移方程：dp[i][j] = min(dp[i-1][j],dp[i][j]) + grid[i][j]
  4. 初始化：根据题意！因为要求最小值，并且有需要最开始的值正常走，那么将第一行 0 1 和第一列 1 0 置为0,其他置为无穷大（建议画图理解）
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int n = grid.size(),m = grid[0].size();//注意本题初始化是：将第一行 0 1 和第一列 1 0 置为0,其他置为无穷大vector<vector<int>> dp(n+1,vector<int>(m+1,INT_MAX));//多创建一行一列，并初始化为INT_MAX，这样就不要遍历第一行，第一列初始化了！//再将 0 1 和 1 0 位置置为0 dp[0][1] = dp[1][0] = 0;for(int i = 1; i <= n;i++){for(int j = 1 ; j <= m;j++){dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i-1][j-1];}}return dp[n][m];}
};class Solution {
public:int minPathSum(vector<vector<int>>& grid) {//思想和 珠宝的最高价值 基本一样，只不过，状态表示以及转移方程不一样//dp[i][j]；到达 i j 位置时，能获取的最小路径和//dp[i][j] = min(dp[i - 1][j],dp[i][j-1]) + frame[i-1][j-1] //其中的frame[i-1][j-1]本质就是frame[i][j]，这不过在循环中因为dp多加一行一列int n = grid.size(),m = grid[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1,INT_MAX));dp[0][1] = 0;//这里不能剩，因为对于第一个元素来说初始化来说，要使用到0，而非INT_MAXfor(int i = 1; i <= n;i++){for(int j = 1; j <= m;j++){dp[i][j] = min(dp[i - 1][j],dp[i][j-1]) + grid[i-1][j-1];}}return dp[n][m];}
};

地下城游戏♟️

题目⭐：

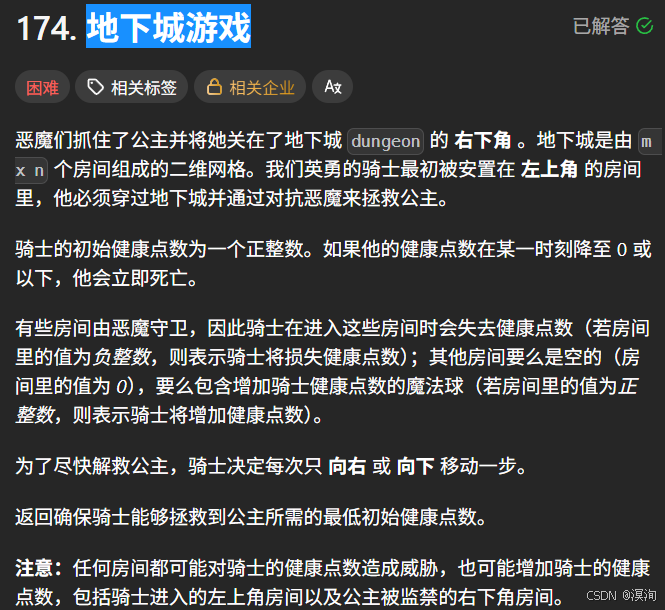
在这里插入图片描述

分析题目并提出，解决方法🛹：

在这里插入图片描述
通过下图来进行分析题目：
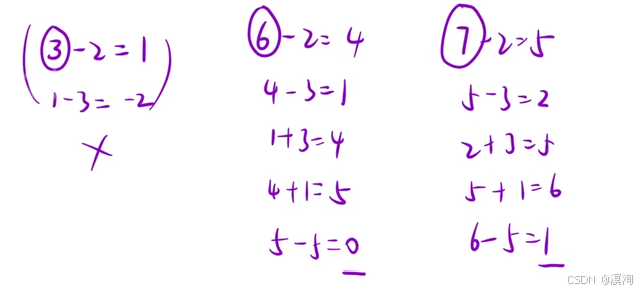
在这里插入图片描述

题解核心逻辑🫏：

  1. 状态表示：经验 + 题目要求
    1. 以某个位置为结尾，。。。不能使用因为从上图三个例子来看到达 i j 位不仅仅只受之前的状态影响，还受后续状态的影响，也就是在第一个位置只用3就能到达，而到了下一个位置这个3就不够了，需要6了，所以这就代表了它不仅仅受前面的影响还受后续的影响，所以这样的状态表示就无法推导状态方程（无后效性）！！！！
      在这里插入图片描述
    2. 以某个位置开始，。。。
      1. dp[ i ][ j ]从 i j 位置出发，到达终点所需的最低初始健康点数
      2. 这题也是遇到的第一个 以某个位置起始 的状态表示，所以有些时候进行分析题目后发现无法快速的退出答案不妨换个思路。
  2. 状态转移方程
    1. 现在知道了状态表示：以 i j 位置开始，到达终点所需的最低健康点数，那么分析题目推导状态方程式：
    2. dp[ i ][ j ] = min(dp右边位置的最低，dp下边位置的最低) - 当前位置的值
    3. 细节的问题：如果当前的值过大，导致dp值变成负数，也就是负的最小健康点数，这是存在问题的，分析题目可知若出现这种情况就将当前值填充为1即可，因为不可能为负数，而1刚好是最小的健康点数
    4. 此处就进行和1进行取较大值，就能快速的填充1（就不需要进行比较了）
  3. 初始化
    1. 填写1的原因是：为了保证第一个位置的值时正确的，填充1代表最小健康点值为1
      在这里插入图片描述
  4. 填表顺序：从下往上，从右往左，因为状态转移方程需要
  5. 返回值 0 0（也就是开始初始化到达终点的最小健康点数）
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int n = dungeon.size(),m = dungeon[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1,INT_MAX));dp[n-1][m] = 1;dp[n][m-1] = 1;for(int i = n - 1;i >= 0;i--){for(int j = m - 1; j >=0 ;j--){dp[i][j] = min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j];dp[i][j] = max(dp[i][j],1);//通过与1进行求最大值，保证健康值最低为1,不为负数}}return dp[0][0];}
};

本题注意点：通过一个max函数来快速的进行比较并赋值、并且不同于之前的本题是以 i j 为开始，而非结束

http://www.dtcms.com/a/395818.html

相关文章：

  • 三.上网行为安全
  • k个一组翻转链表
  • Super分区和动态分区
  • 2026华清远见新品发布会：聚焦人工智能嵌入式物联网，打造“虚实融合•软硬协同“智能化教育新生态！
  • 09 - spring security加载流程
  • 【大前端】Android：读取剪切板与禁用剪切板复制功能（完整指南）
  • 第18讲 机器学习与深度学习
  • 数据结构 05（线性：栈和队列）
  • RAG系统嵌入模型怎么选？选型策略和踩坑指南
  • 机器学习 vs. 动力学模型，Ai2 最新研究：仅需 2 分钟，ACE2 可完成一次 4 个月季节预报
  • RNN循环神经网络详解
  • 【Nginx开荒攻略】深入解析Nginx进程管理与信号控制：从原理到实战
  • MySQL与Redis面试问题详解
  • 鸿蒙Next IPC Kit详解：构建高效进程间通信的完整指南
  • 【开题答辩全过程】以 基于springboot的高校疫情防控系统为例，包含答辩的问题和答案
  • Centos7 命令行使用nmcli重置网络配置
  • 如何计算sequence粒度的负载均衡损失
  • 学财税大数据应用，需要考CPA/税务师吗？
  • RAG全栈技术——文档加载器
  • 如何理解Service Mesh(服务网格)
  • android9适配camera gc02m1
  • 【十天成长计划】BoostKit初级班 开班啦！——陪伴式学习，阶梯式成长
  • 【图文详解】强化学习核心框架、数学基础、分类、应用场景
  • Rust简介
  • golang和rust内存分配策略
  • 简历项目之无人机图像目标识别
  • pantherx2 armbian librga-rockchip librga.so 编译安装方法
  • 【精品资料鉴赏】189页工程车辆集团数字化转型SAP解决方案
  • 算法 --- 多源 BFS
  • 15.Linux 硬盘分区管理