CCF-CSP-S 2021 初赛解析

注：完善程序的公式还没有转换完成，后续会陆续更新

（一）单项选择题

第一题

答案：Ｂ

解析：

ls：list列表，用于列出目录下文件和子目录。

cp：copy复制。
cd：change directory，切换目录。
all：linux中无此命令。

第二题

答案：B

解析：

二进制运算，逢二进一。

第三题

答案：Ａ

解析：

调用栈描述的是函数之间的调用关系。它由多个栈帧（stack frame）组成，每个栈帧对应着一个未运行完的函数，栈帧中保存了该函数的返回地址和局部变量，因而不仅能在执行完毕后找到正确的返回地址，还保证了不同函数间的局部变量互不相干，因为不同函数对应着不同的栈帧。

第四题

答案：C

解析：

稳定性：

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

简单来说，一个无序序列8 2 4 7 2 9 5 8 5排成单调递增序列相同的元素排序后先后位置不变即为有序，例如当前两个8的下标为0和7，如果排序后下标为0的8的下标还比下标为8的下标小，那么即为稳定，但须把所有相同元素全部遍历后，才可证明其稳定。

第五题

答案：C

解析：

前两个数比较，大的最大，小的最小。剩下的2n-2个每两个比较，大的与最大的比较，小的与最小的比较。合计:1+(2n-2)/2*3=3*n-2

第六题

答案：C

解析：

h(0)=0%11=0

h(1)=1%11=1

h(2)=4%11=4

h(3)=9%11=9

h(4)=16%11=5

h(5)=25%11=3

h(6)=36%11=3，地址3、4、5被占，存在6

h(7)=49%11=5，地址5、6被占，存在7

第七题

答案：C

解析：

简单无向图：没有自环和重边，可以有环。N个点的边数是n*(n-1)/2，所以9个点是36条边，要求非连通，还需要一个不连通的点，所以一共10个点。

第八题

答案：B

解析：

高度	结点总数
1	1 = -1
2	3 =
3	7 =
n

所以高度10的结点数为1023，11为2047，所以2021在前10层满，11层不满的状态，所以至少高度为11。

第九题

答案：D

解析：

前序遍历：根（左）右

中序遍历：（左）根右

所以应去掉左子树。

A：题干说有且仅为，A是D的一种特殊情况，所以不完全

B：根节点没有左子树不代表它的子节点没有左子树

C：直接排除

第十题

答案：Ａ

解析：

考了逆序对的概念，什么叫做逆序对呢？给定一个序列a1，a2，a3，a4，a5，．．．，an 如果存在i<j并且 ，那么我们称之为逆序对。

DACFEB一共7个逆序对。一次交换改变一个逆序对。所以改7回。

也可以看成排序，冒泡排序，最少次数。

第十一题

答案：A

解析：

观察程序可以发现，每次递归都提了个5拿出来乘，排除t=1时做的初始化，一共是22个5相乘，也就是 。

快速幂：

则s(23)=5*s(22)%23=5*5*s(21)%23%23= %23=1

定理：(x*y)%c=((x%c)*(y%c))%c

%23=2

这里就是可以把 %23拆成 %23

%23=4

%23=16

%23=3

%23=( * * )%23=3*4*2%23=1

第十二题

答案：C

解析：

理解为一个二叉树，第n层有2*n个节点，前n层节点总数为:1+2+4+……+ =

计算时间复杂度的规则：不看常数，只看最高次项。

因此：O（F（n）） = O（ ）

第十三题

答案：C

解析：

用动态规划的思想做此题

设f[i]为前i个苹果，必选第i个苹果，且第i个苹果是选择的最后一个苹果，且不选相邻苹果的方案数

f[1] = 1

f[2] = 1

f[3] = f[1]+1 = 2

f[4] = f[1]+f[2]+1 = 3

f[5] = f[1]+f[2]+f[3]+1 = 5

f[6] = f[1]+f[2]+f[3]+f[4]+1 = 8

f[7] = f[1]+f[2]+f[3]+f[4]+f[5]+1 = 13

f[8] = f[1]+f[2]+f[3]+f[4]+f[5]+f[6]+1=21

答案=f[1]+f[2]+f[3]+f[4]+f[5]+f[6]+F[7]+F[8] = 54

第十四题

答案：C

解析：

先考虑等边三角形情况

则a=b=c=1,2,3,4,5,6,7,8,9,此时有9个

再考虑等腰三角形情况，若a,b是腰，则a=b

当a=b=1时，c<a+b=2，则c=1，与等边三角形情况重复；

当a=b=2时，c<4，则c=1,3（c=2的情况等边三角形已经讨论了），此时有2个；

当a=b=3时，c<6，则c=1,2,4,5，此时有4个；

当a=b=4时，c<8，则c=1,2,3,5,6,7，有6个;

当a=b=5时，c<10，则c=1,2,3,4,6,7,8,9，有8个；……

由加法原理知共计有2+4+6+8+8+8+8+8=52个

同理，若a,c是腰时，c也有52个，b，c是腰时也有52个

所以n共有9+3*52=165个。

第十五题

答案：B

解析：

这里可以使用迪杰斯特拉，路径为A-C-E-H-J。     

单源最短路径：Dijkstra算法，把节点分成两个集合，已确定最短路的S集合和未确定最短路的U集合，每次按最短路径长度的递增次序依次把U集合的节点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。

(二）阅读程序

（1）

前导知识：

球冠：球面被平面所截得的一部分叫做球冠，截得的圆得的圆叫做球，垂直于截面的直径被截得的一段叫做球冠的高，如图球冠。

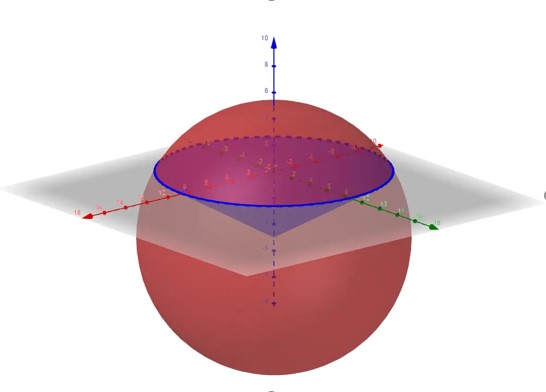
体积V=

r为球的半径，a为拱底圆半径，h为拱高

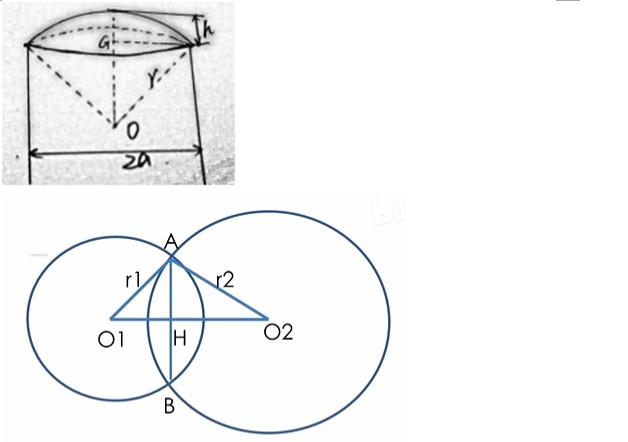
H是线段AB与线段O1O2的交点，设线段O1O2的长度为d，设线段O1H的长度为x，则有：

推出：

球O1部分的球冠高度h=r1-x

注：x表示的是O1H这条线段

球冠就是O1这个球H以上的部分

接下来我们试着推一下球冠体积之和：

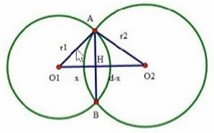
由图可以求得球O1的球冠参数为r= ,

球O2的球冠的参数为r= ,

h=

带入上述的球冠体积公式得：

V=

=

  +  

分析程序主要内容：

求两个球体相交的体积：两个球体的球心距离是dis

1. dis大于两个球体半径和，不想交
2. dis小于等于两个球体的半径差，打球包含小球，相交体积是小球体积
3. 否则相交，计算两个球冠和

主体程序如下：

#include <iostream>#include <cmath>using namespace std;const double r = acos(0.5);//r是PI/3，是60度，反余弦函数，博客自己查int a1, b1, c1, d1;int a2, b2, c2, d2;inline int sq(const int x) { return x * x; }inline int cu(const int x) { return x * x * x; }int main(){cout.flags(ios::fixed);cout.precision(4);//精度：四位小数cin >> a1 >> b1 >> c1 >> d1;//球心位置，半径cin >> a2 >> b2 >> c2 >> d2;//球心位置，半径int t = sq(a1 - a2) + sq(b1 - b2) + sq(c1 - c2);//两个球球心距离(d)的平方if (t <= sq(d2 - d1)) cout << cu(min(d1, d2)) * r * 4;//情况1:大球包含小球else if (t >= sq(d2 + d1)) cout << 0;//情况2:两球不相交else {//情况三:相交double x = d1 - (sq(d1) - sq(d2) + t) / sqrt(t) / 2;//球冠高，h1double y = d2 - (sq(d2) - sq(d1) + t) / sqrt(t) / 2;//球冠高，h2cout << (x * x * (3 * d1 - x) + y * y * (3 * d2 - y)) * r;//相交体积}cout << endl;return 0;}

开始答题：

16．✔

解析：

输入的球的位置都是int，int平方后还是int，int转化成double，4个字节变8个字节，值不变。

17.❌

解析：

前面计算都是int类型，sqrt是double类型，先计算sqrt再/2可以避免c++中的整除，调换后会有误差。

18.❌

解析：

sq函数接收时是int，而x，y都是double类型，这样会导致把浮点数转化成整数，导致计算错误。

19.✔

解析：

这组测试数据是第三种情况，观察程序，进行模拟即可。

PI=3.1415926

r=1.04719753

d1 = 1 , d2 = 1 , t = 1

x = d1-(sq(d1)-sq(d2)+t)/sqrt(t)/2

y = d2-(sq(d2)-sq(d1)+t)/sqrt(t)/2

x=0.5 , y=0.5

输出(x*x*(3*d1-x)+y*y*(3*d2-y))*r

       =((0.5*0.5*(3*1-0.5)+0.5*0.5*(3*1-0.5))*1.0471953=1.30899692

20.D

解析：

还是模拟程序，很简单：

PI=3.1415926

r=1.04719753

d1 = 1

d2 = 2

t = 0//两个球心重合

小球被大球包含

if(t<=sq(d2-d1)) cout<<cu(min(d1,d2))*r*4

输出 1*r*4 = 4.18879013

注意程序使用了cout.setpricision(4)，所以需保留前4位，输出4.1888

21.C

解析：

没有啥说的了，就是求相交部分。

两个球的体积并=两个球的总体积-两个球的体积交（重复部分）

（2）

程序主要内容：

分治法求最大子段和。区间[l,r]，中点mid=(l+r)/2的最大子段和有三种可能性。子段在[l,mid]，在[mid+1,r]，或者子段包含中点mid。前两种情况可递归求解，第三种情况，是[l,mid]最大的后缀和加上[mid+1,r]最大的前缀和。

solve1函数（+号重载）返回的结构体的4个参数，分别是当前区间的：

h:最大前缀和（若小于0则为0）

j:最大子段和（若小于0则为0）

m:最大后缀和（若小于0则为0）

w:区间和

solve2函数计算经过中点的最大子段和（左区间最大后缀和加上右区间最大前缀和），再与左区间和右区间的最大子段和作比较，求出当前区间最大子段和。

代码（注释）：

#include <algorithm>#include <iostream>using namespace std;int n , a[1005];struct Node{//h:最大前缀和（若小于0则为0），j：最大子段和（若小于0则为0）int h , j , m , w;//m:最大后缀和（若小于0则为0），w：区间和Node(const int _h,const int _j,const int _m,const int _w):h(_h),j(_j),m(_m),w(_w){}Node operator+(const Node &o) const{//+号重载return Node(max(h,w+o.h),//求区间最大前缀和（若小于0则为0），w：区间和max(max(j,o.j),m+o.h),//左区间最大子段和，右区间最大子段和，左区间最大后缀和+右区间最大前缀和max(m+o.w,o.m),//区间最大后缀和w+o.w);//求和}                                               };Node solve1(int h , int m){//参数是区间左端点和右端点if(h>m)return Node(-1,-1,-1,-1);if(h==m)//如果区间只有1个元素return Node(max(a[h],0),max(a[h],0) ,max(a[h],0),a[h]);int j = (h+m)>>1;//分治点return solve1(h,j) +solve1(j+1,m);}int solve2(int h , int m)//参数：区间左边界和有边界{if(h>m)     return -1;//区间不存在if(h==m)  return max(a[h],0);//区间只有1个元素，递归返回点int j = (h+m) >>1;//中点int wh = 0 , wm = 0;//最大后缀和，最大前缀和int wht = 0 , wmt = 0;//累计后缀和，累计前缀和for(int i = j ; i>=h ; i--){//计算左区间[h,j]的最大后缀和wht += a[i];//累计后缀和wh = max(wh,wht);//滚动比较，最小是0}return max(max(solve2(h,j),solve2(j+1,m)),wh+wm);//三种情况比较出最大值} //左区间最大子段和，右区间最大子段和，左区间最大后缀和+右区间最大前缀和int main(){cin>>n;for(int i = 1 ; i<=n ; i++) cin>>a[i];cout<<solve1(1,n).j<<endl;cout<<solve2(1,n)<<endl;return 0;}

22.✔

解析：

两个函数的功能相同，通过模拟与代码分析可知

23.❌

解析：

区间不存在最多一次，后面就结束运算了

24.❌

解析：

程序分析可知，最大子段和不是7。

25.B

解析：

以n=256举例，第1层1次，第2层2次，第3层4次，一直加到深度log256=8。

1+2+4+16+32+64+128的约为256，与O（n）相当。

26.C

解析：

每一层都要遍历n个数字，有log n层。

27.B

解析：

从下标0开始，1-9是最大子段和，所以选择B。

（3）

先分析一下程序：

详细注释版程序：

#include <iostream>#include <string>using namespace std;// Base64编码表（64个字符）char base[64];// Base64解码表（256个ASCII字符的映射）char table[256]; /*** 初始化Base64编码表和解码表*/void init(){// 1. 构建Base64编码表// 前26个大写字母 A-Zfor(int i = 0; i < 26; i++) base[i] = 'A' + i; // 接着26个小写字母 a-zfor(int i = 0; i < 26; i++) base[26+i] = 'a' + i; // 然后10个数字 0-9for(int i = 0; i < 10; i++) base[52+i] = '0' + i; // 最后两个特殊字符 + 和 /base[62] = '+', base[63] = '/'; // 2. 构建Base64解码表（逆向映射）// 初始化为全0xff表示无效字符for(int i = 0; i < 256; i++) table[i] = 0xff; // 填充有效字符的映射for(int i = 0; i < 64; i++) table[base[i]] = i; // '=' 填充符映射为0table['='] = 0; }/*** Base64编码函数* @param str 原始字符串* @return Base64编码后的字符串*/string encode(string str) {string ret; // 存储编码结果// 处理每3个字节为一组int i;for(i = 0; i+3 <= str.size(); i += 3) {// 第一个Base64字符：取第1个字节的高6位ret += base[str[i] >> 2]; // 第二个Base64字符：第1个字节低2位 + 第2个字节高4位ret += base[(str[i] & 0x03) << 4 | str[i+1] >> 4]; // 第三个Base64字符：第2个字节低4位 + 第3个字节高2位ret += base[(str[i+1] & 0x0f) << 2 | str[i+2] >> 6]; // 第四个Base64字符：第3个字节低6位ret += base[str[i+2] & 0x3f]; }// 处理剩余不足3个字节的情况if(i < str.size()) {// 第一个Base64字符：剩余第1个字节的高6位ret += base[str[i] >> 2]; if(i+1 == str.size()) { // 只剩1个字节// 第二个Base64字符：剩余字节低2位 + 4个0位ret += base[(str[i] & 0x03) << 4]; // 填充两个'='ret += "=="; } else { // 剩2个字节// 第二个Base64字符：第1个字节低2位 + 第2个字节高4位ret += base[(str[i] & 0x03) << 4 | str[i+1] >> 4]; // 第三个Base64字符：第2个字节低4位 + 2个0位ret += base[(str[i+1] & 0x0f) << 2]; // 填充一个'='ret += "="; }}return ret;}/*** Base64解码函数* @param str Base64编码字符串* @return 解码后的原始字符串*/string decode(string str) {string ret; // 存储解码结果// 处理每4个Base64字符为一组int i;for(i = 0; i < str.size(); i += 4) {// 第一个原始字节：第1个Base64字符全部6位 + 第2个Base64字符高2位ret += table[str[i]] << 2 | table[str[i+1]] >> 4; if(str[i+2] != '=') {// 第二个原始字节：第2个Base64字符低4位 + 第3个Base64字符高4位ret += (table[str[i+1]] & 0x0f) << 4 | table[str[i+2]] >> 2; }if(str[i+3] != '=') {// 第三个原始字节：第3个Base64字符低2位 + 第4个Base64字符全部6位ret += table[str[i+2]] << 6 | table[str[i+3]]; }}return ret;}int main(){init(); // 初始化编码/解码表int opt; // 操作选项：0编码，1解码string str; // 输入字符串cin >> opt >> str;// 根据选择执行编码或解码cout << (opt ? decode(str) : encode(str)) << endl;return 0;}

程序作用：

这个程序实现了 Base64 编码和解码功能。Base64 是一种用64个可打印字符来表示二进制数据的方法，常用于在HTTP、电子邮件等文本协议中传输二进制数据。

模拟init初始化：

初始化部分 (init 函数):

创建 Base64 编码表 base[64]，包含大写字母A-Z、小写字母a-z、数字0-9，以及'+'和'/'

创建解码表 table[256]，用于快速查找字符对应的6位值

base char类型数组0-25存的是大写英文字母，26-51是小写，52-61是阿拉伯数字0-9，62，63分别是’+’,’/’。

table char类型数组0-255存的是255=0xff。

table下标‘A’-‘Z’存的是0-25，’a’-‘z’存的是26-51，‘0’-‘9’存的是52-61，‘+’存的是62，‘/’存的是63，’=’存的是0。

也就是说table与base一一对应。

encode（编码函数）：

每3个字节的原始数据转换为4个Base64字符

处理不足3字节的尾部数据，用'='填充

具体步骤:

第一个字符的高6位作为第一个Base64字符

第一个字符的低2位和第二个字符的高4位组合为第二个Base64字符

第二个字符的低4位和第三个字符的高2位组合为第三个Base64字符

第三个字符的低6位作为第四个Base64字符

作用：输入3个字符，编码成4个字节。

for(i = 0; i+3 <= str.size(); i += 3) {

        // 第一个Base64字符：取第1个字节的高6位

        ret += base[str[i] >> 2]; 

        // 第二个Base64字符：第1个字节低2位 + 第2个字节高4位

        ret += base[(str[i] & 0x03) << 4 | str[i+1] >> 4]; 

        // 第三个Base64字符：第2个字节低4位 + 第3个字节高2位

        ret += base[(str[i+1] & 0x0f) << 2 | str[i+2] >> 6]; 

        // 第四个Base64字符：第3个字节低6位

        ret += base[str[i+2] & 0x3f]; 

    }

注：前导零会自动补齐

我们先看这段代码，为什么str在处理第二个字符是要&0x03呢？因为0x03相当于十进制的3，二进制的0011，这要在取后两位时可以通过这个技巧巧妙地完成。&和|是位运算，相当于*与+，举个例子：

1|1=1，1|0=1，0|0=0

1&1=1，1&0=0，0&0=0

decode（解码函数）：

跟上面差不多，只不过是从4个字节编成3个字节，给出另一版的注释，自行理解：

string ret;

       int i;

       for(i = 0 ; i<str.size() ; i+=4){//每4个字符操作1轮

              ret += table[str[i]]<<2|table[str[i+1]]>>4;//第1个字符

              if(str[i+2]!='=')//如不是=号， 生成第2个字符

                     ret += (table[str[i+1]]&0x0f)<<4|table[str[i+2]]>>2;

              if(str[i+3]!='=')//如不是=号，生成第3个字符

                     ret += (table[str[i+2]]<<6|table[str[i+3]]);

       }

       return ret;

总结：

这两个程序就是输出编码或解码，很简单。

开始做题：

28.❌

解析：

有反例：对“QQpc”进行解密，其结果是“A\nB”，\n表示换行符，解密成两行输出。

29.✔

解析：

编码与解码一一对应。

30.❌

解析：

应是小写w

31.B

解析：

因为encode函数每个输入字符访问1次，所以复杂度是O(n)。

32.D

解析：

table[0] = 0xff

table[]的类型是char，即signed char，1个字节，int，即signed int，4个字节

signed char强制类型转化成int，则在前面的三个字节补符号位

补上0xffffff（char的首位为1）

或0x000000（char的首位为0）

unsigned char转化为int，则前面补上0x000000

所以转化后的数值是0xffffffff

是-1的补码

33.D

解析：

输入0是编码，CSP2021csp共10个字符，10%3=1，所以最后输出2个等号，答案应是B或D。B和D只有1个字符不同，是4个字符中的第2个。

所以可以发现不同处是编码1cs时产生的。

输入字符1和c：字符1的后两位+字符c的高四位

      字符1，ASCLL码十进制49，二进制00110001

      第一个str[i]字符1二进制ASCLL码

      &0x03

      结果

      <<4：左移4位，右侧0补齐

      字符c，ASCLL码十进制99，二进制01100011

      第2个str[i+1]字符c二进制ASCLL码

      >>4：右移4位，左侧0补齐

      |：按位或

      结果

      对应十进制22，base[22]是字符W

（三）完善程序

（1）

程序主干内容：

贪心，思维方式类似Dijkstra最短路。有两个集合，一个是已经确定了“最少使用4个数”的节点（数字）集合S集合，一个是未确定“最少使用4个数”的节点（数字）集合U集合。每次，从U集合中找到“最少使用4个数”的节点x，将其放入S集合，同时用x和S集合中的每一个节点i组合，通过加，减，整除，得到数字y的“最少使用4个数”，F[y]=min(F[y],F(x)+F(i))。

起点是F[4]=1，数字4使用4个数最少，使用1个4，每轮找到一个新的“最少使用4个数”的节点。“最少使用4个数”的次数逐渐增加。

完整程序（带注释及答案）：

#include <iostream>

#include <cstdlib>

#include <climits>

using namespace std;

const int M = 10000;

bool Vis[M+1];//Vis[i]为1，标识数字i的“最少使用四个数”已确定

int F[M+1] ;//F[i]，表示数字i的“最少使用4个数”，初始极大值

void update(int &x , int y) {//将x和t的较小值赋值给x，引用语法，函数中可改变值

       if(y<x)

              x = y;

}

int main(){

       int n;

       cin>>n;

       for(int i = 0 ; i<=M ; i++)//最小值，初始赋值极大值

              F[i]  = INT_MAX;//宏，在climits头文件定义

       F[4]  = 1;//第1题，递推起点，F[4]用1个4表示，所有F[]的最小值

       int r = 0;//统计经过多少轮得到答案，程序中没有实际用途。

       while(!Vis[n]) //第二题，n的“最少使用4个数”已确定，推出循环，否则，继续循环

       {

              r++;//统计运行多少轮

              int x = 0;//x是U集合中“最少使用4个数”，最小的数字，初始值为F[0]为极大值

              for(int i = 1 ; i<=M ; i++) //滚动比较，找到U集合中“最少使用4个数”最小的数字

                     if(!Vis[i]&&F[i]<F[x]) //第三题，若i在U集合，并且F值更小，更新x

                            x = i;//选项B不对，见后页

              Vis[x]  = 1;//数字i进S集合的数字组合，已确定“最少使用4个数”，因为S集合的都更小，U集合中i最小

              for(int i = 1 ; i<= M ; i++)//x与所有S集合的数字组合，加减除形成新数，更新新数的F[]

                     if(Vis[i]){//第四题，如果数字i属于S集合

                            int t = F[i]+F[x];

                            if(i+x<=M) update(F[i+x],t);//加法更新

                            if(i!=x)  update(F[abs(i-x)],t)//减法更新

                            if(i%x==0)  update(F[i/x],t);//整除更新

                            if(x%i==0)  update(F[x/i],t);//整除更新

                     }

       }

       cout<<F[n]<<endl;//输出答案

       return 0;

}

34.D

解析：

4只需要一个4即可

35.A

解析：

没有找到n的最小值时，再继续循环。

36.D

解析：

选项B不对，比如r=2时，F[1]、F[8]都是2，一次while处理F[8]，下一次应当处理F[1]，但再进while，r加1变成3，F[1]就没有处理，F[1]=2，若以F[1]为基准x，会计算F[5]=3，但因为未用，所以F[5]的值就会不对。

37.C

解析：

看程序解析。

（2）

此程序看不懂很正常，可以结合AI进行理解

前置知识-笛卡尔树：

笛卡尔树，详细讲解见https://oi-wiki.org/ds/cartesian-tree/

补充一些注解，

小根堆：

将元素按照健值k排序。然后一个一个插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这个树的右链（右链：即从根节点一直往右子树走，经过的结点形成的链）的末端。于是我们执行这样一个过程，从下往上（单调栈，栈底是最小值）比较右链结点与当前节点u的w，

情况1：当前节点u的w比所有右链节点的w小，节点u做根节点，原树做u的左子树。

情况2：如果找到了一个右链上的节点x满足xw<uw

（x的右子节点y满足yw<uw

），就把u接到x的右儿子上，而x原本的右子树（y节点开始的子树）就变成u的左子树。

大根堆：

将元素按照键值k排序。然后一个一个插入到当前的笛卡尔树中。那么每次插入的元素必然在这个树的右链（右链：即从根结点一直往右子树走，经过的结点形成的链）的末端。于是执行这样一个过程，从下往上（单调栈，栈底是最大值）比较右链结点与当前结点u的w，

情况1：当前结点u的w比所有右链的结点的w大，节点u做根节点，原树做u的左子树。

情况2：如果找到了一个右链上的结点x满足xw>uw

​（并且，x的右子节点y满足yw<uw

），就把u接到x的右儿子上，而x原本的右子树(γ节点开始的子树)就变成u的左子树。

前置知识-二叉搜索树：

二叉查找树（Binary Search Tree），（又：二叉搜索树）它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树。

二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

前置知识-树的欧拉序：

树的欧拉序：www.jianshu.com/p/55037ae618ce

完整版程序（带注释）：

#include <iostream>

#include <cmath>

using namespace std;

const int MAXN = 100000 , MAXT = MAXN<<1;

const int MAXL = 18 , MAXB = 9 , MAXC = MAXT/MAXB;

struct node{

       int val;//数列值

       int dep , dfn , end;//深度，欧拉进序号，欧拉回溯返回序号

       node *son[2] ;//son[0] , son[1]分别表示左右儿子

}T[MAXN];

int t , n , b , c , Log2[MAXC+1];

int pos[(1<<(MAXB-1))+5] , Dif[MAXC+1];

node *root , *A[MAXT] , *Min[MAXL][MAXC];

void build(){//建立Cartesian树，大根堆

       static node *S[MAXN+1];//S单调栈，栈底节点val最大，栈顶最小

       int top = 0;//单调栈栈顶

       for(int i = 0 ; i<n ; i++){//依次处理数列元素T[i]

              node *p = &T[i]   ;//p存T[i]地址，指向T[i]

              while(top&&S[top]->val<p->val)//栈非空，T[i]的val比栈顶大

                     p->son[0] = S[top--];//第一题，p的左子树时当前栈顶节点，栈顶弹出

              if(top) //第二题，推出while,如果栈内还有元素，栈顶节点的右儿子是p

                     S[top]->son[1] = p;

              S[++top]  = p;//p进栈

       }

       root = S[1];//栈顶是笛卡尔树的根节点

}

void DFS(node *p) {//构建Euler序列（欧拉序列） ，t是欧拉序列编号

       A[p->dfn = t++] = p;//进p节点，记录p的dfn，欧拉序列记录到p节点，

       for(int i = 0; i<2 ; i++) //最多两个子节点

              if(p->son[i]){//若子节点存在

                     p->son[i]->dep = p->dep + 1;//记录子节点深度

                     DFS(p->son[i]);//深搜进入子节点，子节点的欧拉序列在子节点深搜增加

                     A[t++]  = p;//子节点返回后到p节点，欧拉序列记录到p节点

              }

       p->end = t-1;//p节点的儿子深搜完，返回父节点，记录p的end

       //p的[dfn,end]是子节点的欧拉序列线性空间范围

}

node *min(node *x , node *y) {//比较求出深度最浅的节点

       return x->dep < y->dep?x:y;//第三题

}

void ST_init() {//以b个位基础单元，计算大块的rmq

       b = (int)(ceil(log2(t)/2));//计算b，基础块的节点个数

       c = t/b;//c个大小为b的基础块

       Log2[1]  = 0;

       for(int i = 2 ; i<=c ; i++)//预处理

              Log2[i]  = Log2[i>>1]+1;

       for(int i = 0 ; i<c ; i++){//计算长度为b的基础块极值

              Min[0][i] = A[i*b];//长度为b的块的第一个值

              for(int j = 1 ; j<b ; j++) //与b内的每个值滚动比较，求出深度最浅的

                     Min[0][i] = min(Min[0][i],A[i*b+j]);//填空3

       }//下面计算长度为2b、4b、8b..块的极值

       for(int i = 1 , l = 2 ; l<=c ; i++ , l<<=1) //块的大小b*(2^i)

              for(int j = 0 ; j+l<=c ; j++) //起点：j*b

                     Min[i][j] = min(Min[i-1][j] , Min[i-1][j+(l>>1)]);

}//上：Min[i][j]从j*b开始，连续b*(2^i)个欧拉节点区间最浅的节点

// Min[i][j] 存的是：从第 j 个块开始，连续 2^i 个块的最小值。

void small_init(){//区块预处理

       for(int i = 0 ; i<=c ; i++)//第i个基础块，一共c个基础块，i*b是每块起点

              for(int j = 1; j<b&&i*b+j<t ; j++) //j,块内处理，块内相邻两位比较

                     if(A[i*b+j]->dep<A[i*b+j-1]->dep)//第四题，块内[j]与[j-1]比，右浅置1

                            Dif[i]  |= 1<<(j-1);//Dif[]右边第1位是块内[0]和[1]的深浅关系,这里就是生成一个只有j-1位的二进制数

       for(int S = 0 ; S<(1<<(b-1)) ; S++){//S状态右边起第i位，是1表示块内[i]比[i-1]浅

              int mx = 0 , v = 0;

              for(int i = 1 ; i<b ; i++){

                     v+=(S>>(i-1)&1)?-1:1;//第五题，加减一求相对大小，v是块内[i]位的深度

                     if(v<mx) {//若块内[i]节点(v)更浅，更新最浅节点

                            mx = v;//更新最浅值

                            pos[S] = i;//最浅位置序号，块内第i位

                     }//i循环，从右往左遍历状态S的每一位（代表块内从左往右第i位置），

              }     

       }//滚动求出S中最浅的块内位置

}

node *ST_query(int l , int r){

       int g = Log2[r-l+1];

       return min(Min[g][l] , Min[g][r-(1<<g)+1]);

}

node *small_query(int l , int r){//块内查询

       int p = l/b;//p的基础块的编号

       int S = (Dif[p]>>(l-p*b))&((1<<(r-l))-1);//第六题

       return A[l+pos[S]] ;

}

//第6空，Dif[]那一行的位运算只会在S状态的前面加0，对结果没有影响

//Dif[p]>>(l-p*b))是基础块内区间左端点开始的几个位置需要消掉

//((1<<(r-l))-1)是查询区间一共涉及几个相邻关系。比如r-l=3,是11

node *query(int l , int r){

       if(l>r)

              return query(r,l);

       int pl = l/b , pr = r/b;

       if(pl==pr){//区间在一个块内，用块内查询

              return small_query(l,r);

       }

       else{//分成三个区域，左右两个区间是块内查询，见后页输入2 5查询

              node *s = min(small_query(l,pl*b+b-1),small_query(pr*b,r));

              if(pl+1<=pr-1)//如存在大块，块间查询

                     s = min(s,ST_query(pl+1,pr-1));

              return s;

       }

}

int main()

{

       int m;

       cin>>n>>m;

       for(int i = 0 ; i<n ; i++)

              cin>>T[i].val;

       build();

       DFS(root);

       ST_init();

       small_init();

       while(m--){

              int l , r;

              cin>>l>>r;

              cout<<query(T[l].dfn,T[r].dfn)->val<<endl;

       }

       return 0;

}

其他题过于简单，直接讲解第6题：
int S = (Dif[p]>>(l-p*b))&((1<<(r-l))-1);//第六题

Dif[p]>>(l-p*b)这个就是指截取需要计算，在区间内的位置，把左边的掩码全部剔除。

因为l/b他就相当于当前基数块的第一位，只能整除。L-l/b就是需要计算的区间内的掩码。

1<<(r-l))-1，指保留在长度范围内的掩码

r-l=len，1<<r-l相当于2的len次方，这样r-l+1位是1，其余二进制位都是0，所以再减去1，就是长度内的二进制全是1，这样再按位与，得出S-Dif[p] 中与查询区间 [l, r] 相关的 二进制状态位。

复杂度

大块预处理：

处理n个（欧拉序列）元素，块大小 b=log/2，块的个数n/logn，复杂度为 n/logn*log(n/logn)=n

小块预处理：

状态数为 2^(b-1)个。

总结一下答案：

ADADDC